はじめに、通常、サイクルのpV図のイメージをつかむことが必要である。 そのために等温過程と断熱過程の曲線をなぞることになる。

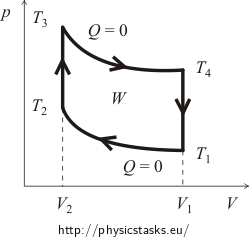
サイクルの効率ηは

\

ここでWは1サイクルで気体が行う仕事から外力が行う仕事（図ではサイクルの線が定義する領域の表面で表現！）を引いたもので、次の図のように定義される。

仕事Wは断熱膨張・圧縮時の圧力と体積の関係から計算できる（等温過程での仕事はもちろんゼロである）。 しかし、この課題では、1サイクルあたりの内部エネルギーの変化の総和が0に等しくなければならない（最初と同じ状態に戻るので、温度も内部エネルギーも変わらない！）ことを利用した方がよいだろう。 熱力学の第一法則によれば、ガスが行う仕事は、供給される熱量Qsupと放出される熱量Qrelの差として表すことができる。 したがって、サイクルの効率を表す式は、

\

まず、供給される熱量Qsupを計算することになる。 断熱過程では熱交換がなく、等温冷却では熱を放出することは明らかである。 つまり、温度T2から温度T3への等温加熱の間だけ熱を供給することになる。 この熱量は気体の物質量nとそのモル熱容量CVを変数として次のように表される：

\

放出熱量Qrelもほぼ同様に表す。 熱の放出は温度T4から初期温度T1に戻る等温冷却の間だけであることはすでに分かっている。 ここで、これらの式をサイクル効率の式に代入すると、すぐに次の式が得られる：

㊞

ここで、与えられた圧縮比

とポアソン比κを用いて、温度差を表現する必要がある。

そこで理想気体の断熱過程の式(ポアソンの法則)pVκ=C=konst…を用います。 ここでCは定数である。 ここで理想気体の状態方程式

から圧力を評価し、これをポアソンの法則に代入する。 ここで定数(CとK)を片側に移し替えて

Ⓐ

このポアソンの法則を両方の断熱過程について適用します。 断熱膨張では

\

の関係が得られ、断熱圧縮では

\

が得られる。ここで最初の式から2番目の式を引き、一方をV1κ – 1、他方をV2κ – 1と因数分解してみる。 6527＞＜8942＞となり、実際に与えられた値を使って温度差を表すことができたことがわかります。 次に、この関係を効率の式に代入すると、最終的に次の式が得られます：

╱╱╱╱。