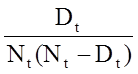の推定
生存関数
や生存曲線を推定するにはいくつかの異なる方法があります。 生存データをモデルするために使用される多くの一般的なパラメトリック手法があり，それらは，母集団での生存時間の分布についてなされる仮定の点で異なる． 2 おそらく最もポピュラーなのは指数分布で，これは参加者が目的のイベントに遭遇する尤度が，その人がどのくらいイベントなしでいたかとは無関係であることを仮定している． 他の分布は、個人がイベントを発症する確率について異なる仮定をしている（すなわち、時間とともに増加、減少、変化する可能性がある）。 生存分析のためのパラメトリック手法の詳細は、Hosmer and Lemeshow とLee and Wang1,3 にあります。
我々はここで2つのノンパラメトリック手法に焦点を当てますが、これはある人がイベントを開発する確率が時間とともにどのように変化するかについて仮定を持ちません。 ノンパラメトリック法を用いて、我々は生存分布または生存曲線を推定しプロットします。 生存曲線は、下図に示すように、しばしばステップ関数としてプロットされます。 時間がX軸に、生存率（危険にさらされている人々の比率）がY軸に表示されています。 生存している参加者の比率は、必ずしも生きている人の比率を表していないことに注意してください（これは関心のある結果が死亡であると仮定しています）。 “生存 “はまた、別の結果イベント（例えば、MIまたは心血管系疾患のない割合）がない割合を指すこともあり、あるいは健康な結果（例えば、がんの寛解）を経験しない割合を表すこともあります。
生存関数
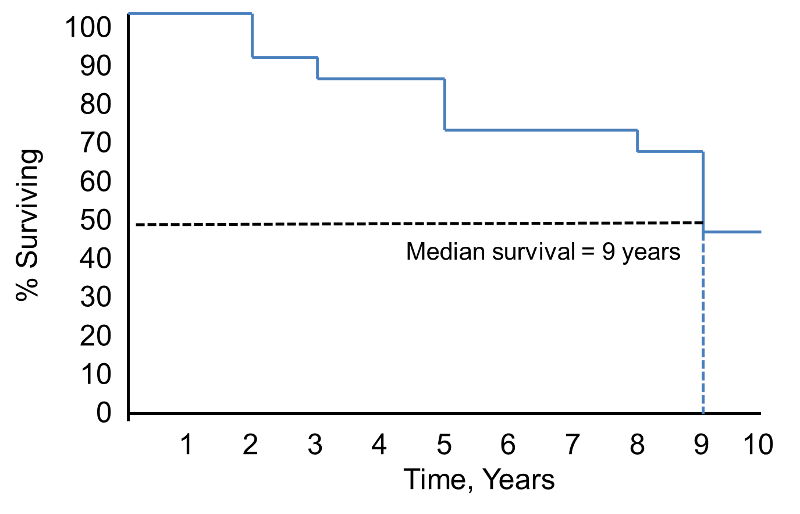
生存確率は2年間は100%で、その後90%に低下することに注意してください。 生存期間の中央値は9年です（すなわち、人口の50％が9年生存する；破線を参照）
例：
死亡までの時間を調査するためにデザインされた小さな前向きコホート研究を考えてみましょう。 この研究には65歳以上の20人の参加者が含まれ、彼らは5年間登録され、死亡するか、研究が終了するか、あるいは研究から脱落するまで（lost to follow-up） 最長24年間追跡される。 そのデータを以下に示します。 この研究では、死亡が6人、完全なフォローアップ（すなわち24年間）が行われた参加者が3人います。 残りの11人は、登録が遅れたり、追跡調査ができなくなったりして、追跡期間が24年未満となっています。
|
参加者識別番号 |
死亡の年 |
の年 最後の接触 |
|---|---|---|
|
1 |
24 |
|
|
2 |
3 |
|
|
3 |
|
11 |
|
4 |
|
19 |
|
5 |
|
24 |
|
6 |
|
13 |
|
7 |
14 |
|
|
8 |
|
2 |
|
9 |
|
18 |
|
10 |
|
17 |
|
11 |
|
24 |
|
12 |
|
21 |
|
13 |
|
12 |
|
14 |
1 |
|
|
15 |
|
10 |
|
16 |
23 |
|
|
17 |
|
6 |
|
18 |
5 |
|
|
19 |
|
9 |
|
20 |
17 |
Life Table (Actuarial Table)
参加者の体験をまとめる一つの方法が生命表である。 またはアクチュアリーテーブルと呼ばれる。 生命表は、保険業界において、平均余命を推定し、保険料を設定するためによく使用される。 ここでは、生物統計学的分析に広く用いられる生命表のうち、コホート生命表や追跡生命表と呼ばれる特殊な生命表に着目する。 追跡生命表は、コホート研究あるいは臨床試験において、あらかじめ定義された追跡期間中に、対象となる事象の発生時あるいは研究終了時のどちらか早いほうまでの参加者の経験を要約したものである
生命表を構築するには、まず追跡時間を等間隔に整理する。 上の表では、我々は最大24年のフォローアップを持っており、5年間隔（0-4年、5-9年、10-14年、15-19年、20-24年）を考慮する。 各間隔の開始時に生存している参加者の数、死亡した数、および各間隔で打ち切られた数を合計する。
|
区間（年） |
区間開始時の生存数 |
区間中の死亡数 |
打ち切り数 |
|---|---|---|---|
|
0-…4 |
20 |
2 |
1 |
|
5-9 |
17 |
1 |
2 |
|
10-14 |
14 |
1 |
4 |
|
15-19 |
9 |
1 |
3 |
|
20-24 |
5 |
1 |
4 |
ライフテーブル分析では以下の表記を使用している。 まず表記法を定義し，次に生命表を構築するためにそれを使用する。
- Nt = 観察区間tの間にイベントがなく，危険と考えられる参加者の数（例, Nt = 観察区間tの間にリスクがないと考えられる参加者の数（例えば、この例では関心のある結果が死亡であるため生存している数）
- Dt = 観察区間tの間に死亡（または関心のあるイベントに苦しむ）する参加者の数
- Ct = 観察区間tの間に打ち切られる参加者の数 Nt* = 観察区間tの間のリスクを有する参加者の平均数
- 【数理生命表を構築するにあたり、しばしば次の前提が用いられる】: まず、関心のある事象（例えば、死亡）は区間の最後に発生すると仮定し、打ち切り事象は区間を通じて一様に（あるいは均等に）発生すると仮定する。 したがって，区間中のリスクのある参加者の平均数Nt*を反映するために，Nt に調整がなされることが多く，これは次のように計算される． Nt* =Nt-Ct/2 (すなわち,
- qt = proportion dying (or suffering event) during interval t, qt = Dt/Nt*
- pt = proportion surviving (remaining event free) interval t, pt = 1-qt
- St, the proportion surviving (or remaining event free) past interval t; this is sometimes called the cumulative survival probability and it is computed as follows.The ratioは，間隔tの期間中の生存（または無事象のまま）割合である． まず，時間 0（開始時間）を過ぎて生存している参加者の比率は， S0 = 1（時間ゼロまたは調査開始時にすべての参加者が生存しているか，またはイベントがない）と定義される． その後の各区間を過ぎて生存している比率は，確率のモジュールで導入された条件付き確率の原理を用いて計算される． 具体的には，参加者が区間1を過ぎても生存している確率は，S1 = p1 である． 参加者が区間2を過ぎて生存する確率は，区間1を過ぎて区間2まで生存しなければならなかったことを意味する： S2 = P(survive past interval 2) = P(survive through interval 2)*P(survive past interval 1), または S2 = p2*S1。 一般にSt+1 = pt+1*St.
追跡生命表の形式を以下に示す。
最初の間隔、0-4年について。 最初の区間（0-4年）の開始である時間0に、20人の参加者が生存しているか、または危険にさらされている。 2人の参加者がその区間で死亡し，1人が打ち切られる． 我々は，その区間で打ち切られた参加者の数の補正を適用して，Nt* =Nt-Ct/2 = 20-(1/2) = 19.5を生成する． 残りの列の計算は、表中にあります。 参加者が4年、または最初の区間を過ぎて生存する確率は、S4 = p4 = 0.897.
2番目の区間、5-9年については、S4 = p4 = 0.897.である。 危険数は, 前の区間 (0-4年)における危険数から死亡して打ち切られる数を引いたものである (すなわち, Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17).また, 危険数は, 最初の区間における危険数から死亡して打ち切られる数を引いたものである。 参加者が9年以上生存する確率は、S9 = p9*S4 = 0.937*0.897 = 0.840です。
|
Interval in Years |
Number At Risk During Interval, Nt |
Average Number At Risk During Interval.これは平均的なリスク数で、1年ごとのインターバルのことである。 Nt* |
インターバル中の死亡数、Dt |
フォローアップのための損失。 Ct |
Proportion Dying During Interval, qt |
Am Among those at Risk, Proportion Surviving Interval.Decimal.Of.Ct Protection Dying Differential Dying Ct |
生存確率 St |
|---|---|---|---|---|---|---|---|
|
0-4 |
20 |
2 |
1 |
2/19.5 = 0.103 |
1-0.103 = 0.897 |
1(0.897) = 0.897 |
|
|
5-9 |
17 |
17-(2/2) = 16.0 |
1 |
2 |
1/16 = 0.063 |
1-0.063 = 0.937 |
(0.897)(0.937)=0.840 |
完全追従生命表は以下の通りです。
|
Interval in Years |
Number At Risk During Interval, Nt |
Average Number At Risk During Interval.Ntは以下の通り。 Nt* |
インターバル中の死亡数、Dt |
フォローアップのための損失。 Ct |
Proportion Dying During Interval, qt |
Among at Risk.Of Those at Risk.Ct と Ct の間に死亡する割合。 生存割合 間隔, pt |
生存確率 St |
|
|---|---|---|---|---|---|---|---|---|
|
0-4 |
20 |
19.0 |
1.5 |
2 |
1 |
0.103 |
0.897 |
0.897 |
|
5-9 |
17 |
16.0 |
1 |
2 |
0.063 |
0.937 |
0.840 |
|
|
10-14 |
14 |
12.0 |
1 |
4 |
0.083 |
0.917 |
0.770 |
|
|
15-19 |
9 |
7.5 |
1 |
3 |
0.133 |
0.867 |
0.668 |
|
|
20-24 |
5 |
3.0 |
1 |
4 |
0.333 |
0.667 |
0.446 |
この表は、時間を等間隔に分割した場合の追認生命表を、保険数理方式で作成したものである。
Kaplan-Meier (Product Limit) Approach
上に示した生命表法の問題は、特にサンプルが小さい場合、区間の構成によって生存確率が変化しうるということです。 Kaplan-Meier approachは積限界アプローチとも呼ばれ、イベントが発生するたびに生存確率を再推定することでこの問題に対処する一般的なアプローチである
Kaplan-Meier approachの適切な使用は、打ち切りが関心イベントを発症する可能性から独立しており、生存確率が研究の早期および後期に募集された参加者で同等であるという仮定に基づいている。 複数のグループを比較する場合、これらの仮定が各比較グループで満たされていること、そして、たとえば、打ち切りがあるグループと別のグループでより起こりやすいわけではないことも重要です
下の表は、生命表法を用いて上で提示された同じデータを提示するのにKaplan-Meier法を使用しています。 我々は時間=0、生存確率=1で表を開始することに注意してください。 Time=0 (ベースライン、または研究の開始)では、すべての参加者が危険にさらされ、生存確率は1（または100%）である。 Kaplan-Meier アプローチでは，生存確率は St+1 = St*((Nt+1-Dt+1)/Nt+1) を用いて計算される． Kaplan-Meier 法を用いた計算は，数理生命表法を用いた計算と同様であることに注意されたい． 主な違いは時間間隔であり，すなわち，数理生命表法では等間隔の時間間隔を考えるが，Kaplan-Meier法では，観察されたイベント時間と打ち切り時間を用いる。 生存確率の計算は、表の最初の数行で詳述されている。
カプラン・マイヤー法による生命表
|
Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time, 年 |
リスクのある数 Nt |
死亡の数 Dt |
打ち切り数 Ct |
生存確率 St+1 = St*((Nt+1-))Dt+1)/Nt+1) |
|---|---|---|---|---|
|
0 |
20 |
|
||
|
1 |
20 |
1 |
|
1*((20-1)/20) = 0.950 |
|
2 |
19 |
|
1 |
0.950*((19-0)/19)=0.950 |
|
3 |
18 |
1 |
|
0.950*((18-1)/18) = 0.897 |
|
5 |
17 |
1 |
|
0.897*((17-1)/17) = 0.844 |
|
6 |
16 |
|
1 |
0.844 |
|
9 |
15 |
|
1 |
0.844 |
|
10 |
14 |
|
1 |
0.844 |
|
11 |
13 |
|
1 |
0.844 |
|
12 |
12 |
|
1 |
0.844 |
|
13 |
11 |
|
1 |
0.844 |
|
14 |
10 |
1 |
|
0.760 |
|
17 |
9 |
1 |
1 |
0.676 |
|
18 |
7 |
|
1 |
0.676 |
|
19 |
6 |
|
1 |
0.676 |
|
21 |
5 |
|
1 |
0.676 |
|
23 |
4 |
1 |
|
0.507 |
|
24 |
|
大きなデータセットではこれらの計算が退屈に感じられるでしょう。 しかし、これらの分析はSASのような統計計算プログラムによって生成することができる。 また，データを時間ごとに整理し，イベントの数と打ち切り時間をまとめると，生存確率を計算するためにExcelを使用することもできる。
生命表からKaplan-Meier生存曲線を作成できます。
上のデータのKaplan-Meier生存曲線
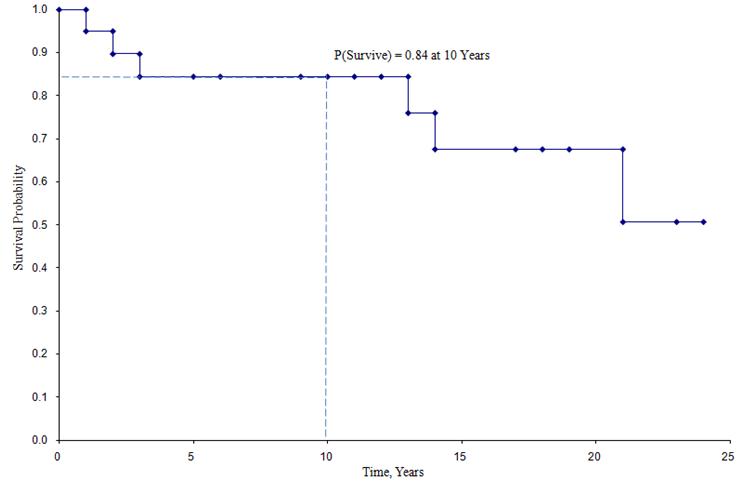
上に示した生存曲線で、記号は各イベント時間、つまり死亡または打ち切られた時間を表します。 生存曲線から、X軸に10年を置いてY軸に読み上げることにより、参加者が10年以上生存する確率を推定することもできます。 10年以上生存している参加者の比率は84%で、20年以上生存している参加者の比率は68%です。 生存期間の中央値は、Y軸に0.5をとり、X軸に読み替えることで推定される。
生存確率の標準誤差と信頼区間推定値
特定の時間における生存確率と中央値生存時間のこれらの推定値は点推定値であり、そのように解釈されるべきです。 多くの統計計算パッケージで生成できる生存確率の標準誤差と信頼区間推定を生成する公式があります。 生存推定値の標準誤差を推定する一般的な公式は、Greenwoods5公式と呼ばれ、次のとおりです：
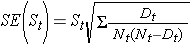
量 
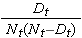が、関心時間（すなわち、関心時間以前のすべての時間にわたる累積、下の表の例参照）までに生じるリスクでの数（Nt）と死亡の数（Dt）の合計される.この式で、生存確率を推定するために、標準誤差の計算を行います:
は、関心時間の間の死亡の数とリスクでの数の合計です。 標準誤差は，下表のデータの生存推定について計算される． 最後の列は、誤差の範囲であり、95%信頼区間推定値（すなわち、St ± 1.96 x SE(St)）を計算するために使用される量 1.96*SE(St)を示していることに注意してください。
生存推定値の標準誤差
|
Time, 年 |
危険数 Nt |
死亡数 Dt |
生存率 確率 St |
|
|
|
1.96*SE (St) |
|---|---|---|---|---|---|---|---|
|
0 |
20 |
1 |
|
|
|
||
|
1 |
20 |
1 |
0.950 |
0.003 |
0.003 |
0.049 |
0.096 |
|
2 |
19 |
|
0.950 |
0.000 |
0.003 |
0.049 |
0.096 |
|
3 |
18 |
1 |
0.897 |
0.003 |
0.006 |
0.069 |
0.135 |
|
5 |
17 |
1 |
0.844 |
0.004 |
0.010 |
0.083 |
0.162 |
|
6 |
16 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
9 |
15 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
10 |
14 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
11 |
13 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
12 |
12 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
13 |
11 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
14 |
10 |
1 |
0.760 |
0.011 |
0.021 |
0.109 |
0.214 |
|
17 |
9 |
1 |
0.676 |
0.014 |
0.035 |
0.126 |
0.246 |
|
18 |
7 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
19 |
6 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
21 |
5 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
23 |
4 |
1 |
0.507 |
0.083 |
0.118 |
0.174 |
0.341 |
|
24 |
3 |
|
0.507 |
0.000 |
0.118 |
0.174 |
0.341 |
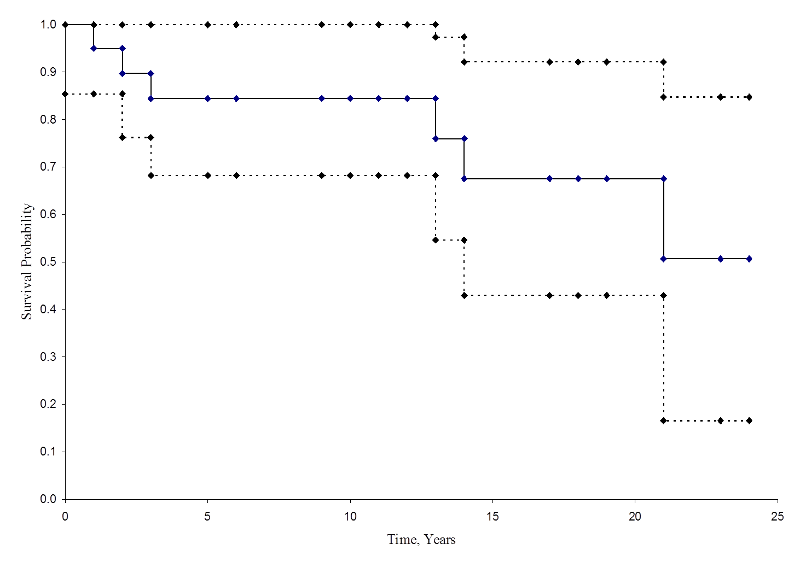
下の図で推定値と信頼区間をまとめてみた。 Kaplan-Meier生存曲線は実線で、95％信頼限界は点線で示されています。
Kaplan-Meier Survival Curve With Confidence Intervals
Cumulative Incidence Curves
研究者によっては、関心のあるイベントを経験する累積確率を示す生存曲線とは対照的に、累積発生率曲線を作成することを好む人がいます。 累積罹患率または累積故障確率は，1-Stとして計算され，Kaplan-Meier 法を用いた生命表から簡単に計算することができる． 上の例の累積故障確率を下表に示す。
累積故障確率を用いた寿命表
|
Time, 年 |
危険数 Nt |
死亡数 Dt |
個体数 打ち切り Ct |
生存確率 St |
失敗確率 1- の場合St |
|---|---|---|---|---|---|
|
0 |
20 |
|
|||
|
1 |
20 |
1 |
|
0.950 |
0.050 |
|
2 |
19 |
|
1 |
0.950 |
0.050 |
|
3 |
18 |
1 |
|
0.897 |
0.103 |
|
5 |
17 |
1 |
|
0.844 |
0.156 |
|
6 |
16 |
|
1 |
0.844 |
0.156 |
|
9 |
15 |
|
1 |
0.844 |
0.156 |
|
10 |
14 |
|
1 |
0.844 |
0.156 |
|
11 |
13 |
|
1 |
0.844 |
0.156 |
|
12 |
12 |
|
1 |
0.844 |
0.156 |
|
13 |
11 |
|
1 |
0.844 |
0.156 |
|
14 |
10 |
1 |
|
0.760 |
0.240 |
|
17 |
9 |
1 |
1 |
0.676 |
0.324 |
|
18 |
7 |
|
1 |
0.676 |
0.324 |
|
19 |
6 |
|
1 |
0.676 |
0.324 |
|
21 |
5 |
|
1 |
0.676 |
0.324 |
|
23 |
4 |
1 |
|
0.507 |
0.493 |
|
24 |
3 |
|
3 |
0.507 |
0.493 |
下図は、上記の研究に登録した参加者の累積死亡発生率を示しています。
Cumulative Incidence Curve
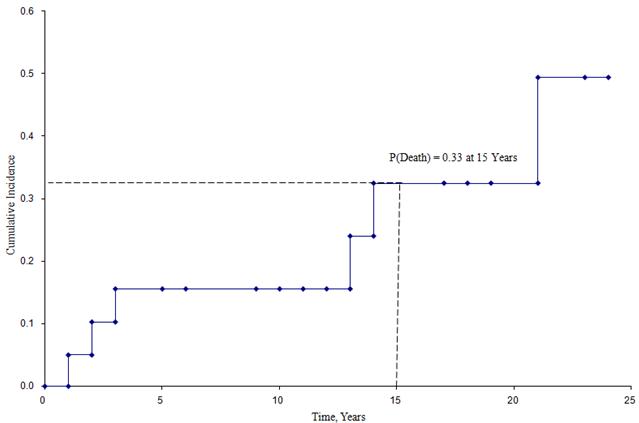
この図から、ある時点までに参加者が死亡する可能性を推定することができる。 例えば、15年目の死亡確率は約33%である（破線を参照）。
トップへ戻る｜前のページ｜次のページ
へ