次の章へ。 グラフ PyGraph
Graphs in Python
Origins of Graph Theory
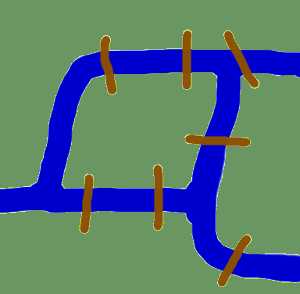Pythonで実際にグラフの実装を始める前に、そしてグラフを扱うPythonモジュールの導入を始める前に、我々はグラフ理論の起源に専念したいと思います。 ケーニヒスベルクは当時プロイセンの都市であった。 その町をプレゲル川が流れ、2つの島をつくっていた。 街と島は、図のように7つの橋で結ばれていた。 この町の住民たちは、「町の各エリアを回りながら、それぞれの橋を一度だけ渡って町を散策することはできないだろうか」という問いに心を動かされた。 どの橋も完全に渡っていなければならない。つまり、橋の途中まで歩いて、あとから反対側から残りの半分を渡ることは許されない。 オイラーは1735年にこの問題を解決し，それが不可能であることを証明した． オイラーは1735年にこの問題を解決し、不可能であることを証明した。彼は、それぞれの土地領域内の経路の選択は重要ではなく、重要なのは橋を渡る順序（あるいは順番）だけであることを発見したのである。 彼は、不要な事実を排除し、陸地とそれを結ぶ橋に焦点を当て、問題を抽象化して定式化したのである。 こうして、グラフ理論の基礎ができあがった。 土地」を頂点、「橋」を辺とすると、問題をグラフに「還元」したことになります。
Pythonによるグラフ理論入門
Pythonによるグラフの表現について考察する前に、グラフとその構成要素についての一般論を紹介します。 この図では、ノード「a」はノード「c」とつながっているが、「a」は「b」とつながっていない。 2つのノードの間を結ぶ線をエッジという。 ノード間のエッジが無向である場合、そのグラフは無向グラフと呼ばれる。 ある頂点（ノード）から別の頂点（ノード）へ向かう辺が有向である場合、そのグラフは有向グラフと呼ばれます。 グラフは非常に理論的に見えるが、多くの現実的な問題はグラフで表現できる。 物理学、生物学、心理学、そして何よりもコンピュータ・サイエンスにおいて、問題や状況をモデル化するためによく利用されます。 コンピュータサイエンスでは、通信網、データ組織、計算装置、計算の流れなどを表すのにグラフが使われます
後者の場合、オペレーティングシステムのファイルシステムのようなデータ組織や、通信網を表すのにグラフが使われます。 Webサイトのリンク構造も、リンクが有向の辺や弧であることから、グラフ、すなわち有向グラフとして見ることができます。
Pythonにはグラフのデータ型やクラスは組み込まれていませんが、Pythonで簡単に実装することができます。 Pythonにはグラフを表現するのに最適なデータ型が1つあり、それは辞書です。 図のグラフは次のように実装できます。
graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }
上の辞書のキーはグラフのノードです。 対応する値は、ノードとリストであり、エッジで接続されています。
辺は、ノードを要素とする 2 タプル、つまり (“a”, “b”) として見ることができます。
すべての辺のリストを生成する関数：このコードは、前に定義したグラフ辞書と組み合わせると、次の出力を生成します：
$ python3 graph_simple.py
見てわかるように、ノード “f” を含む辺は存在しません。 「
次のPython関数は、与えられたグラフの孤立ノードを計算します：この関数をグラフで呼び出すと、「f」を含むリストが返されます。
Graphs as a Python Class
グラフのための関数を書く前に、Python のグラフクラスの実装を最初に見ておきましょう。 以下のクラスのリストを見ると、__init__メソッドで、頂点とそれに対応する隣接頂点を保存するために辞書 “self.__graph_dict” を使用していることがわかります。
このモジュールをスタンドアロンで起動すると、次のような結果が得られます。
Paths in Graphs
あるノードから別のノードへの最短経路を今見つけたい。 この問題の Python コードに来る前に、いくつかの正式な定義を提示する必要があります。
隣接する頂点：
2 つの頂点は、それらが両方とも共通の辺に入射するとき、隣接します。
無向グラフ内のパス：
無向グラフ内のパスは、頂点のシーケンス P = ( v1, v2, … )…, vn ) ∈ V x V x … x Vで、viが1≦i < nでv{i+1}に隣接しているような経路Pをv1からvnまでの長さnの経路と呼ぶ。
単純経路：
頂点の繰り返しがない経路を単純経路と呼ぶ。
例：
(a, c, e) はグラフでは (a,c,e,b) と同じ単純経路と言える。 (a,c,e,b,c,d)はパスですが、ノードcが2回出てくるので単純なパスではありません。
次のメソッドは開始頂点から終了頂点へのパスを見つけます。find_pathメソッドを含むグラフクラスを “graphs.py “として保存すると、 find_path関数がどのように動くか確認することができます。
find_all_pathsメソッドは、開始頂点と終了頂点の間のすべてのパスを見つけることができます。
Degree
グラフの頂点vの次数は、その頂点を結ぶ辺の数で、ループは2回カウントされます。 頂点vの次数はdeg(v)と表記される。 グラフGの最大次数をΔ(G)、最小次数をδ(G)で表すと、その頂点の次数の最大値と最小値になる。
右図のグラフでは、最大次数は頂点cの5、最小次数は孤立頂点fの0です。
グラフの次数がすべて同じであれば、そのグラフは正則グラフです。
次数の和の公式(Handshaking lemma):
∑v ∈ Vdeg(v) = 2 |E|
これは、すべての頂点の次数の和が、辺の数に2を掛けたものに等しいことを意味し、奇数度の頂点の数は偶数にならなければならないと結論付けることができる。 この宣言はハンドシェーキング・レンマと呼ばれる。
The following method calculates the degree of a vertex:
The following method calculates a list containing the isolated vertices of a graph:The methods delta and Delta can be used to calculate the minimum and maximum degree of a vertex respectively ⧏35⧐ 頂点の次数を求めるには、以下の方法を使用します。
Degree Sequence
The degree sequence of an undirected graph is defined as the sequence of its vertexdegrees in a non-increasing order.
以下のメソッドはインスタンスグラフの次数をタプルで返します。
このグラフの次数列は次のような整数の列である。 (5,2,1,1,1,0).
同型のグラフは同じ次数列を持つ。 しかし、次数列が同じ2つのグラフは必ずしも同型とは限りません。
ある次数列が単純なグラフで実現できるかという問題がある。 エルドス＝ガライの定理は、n個の数diの非増加列（fori = 1, ….(fori = 1 … , n) の非増加数列は、数列の和が偶数で以下の条件を満たす場合にのみ、単純グラフの次数数列となります。 まず、数列の要素の和が奇数であるかどうかを調べます。 奇数であれば，Erdös-Gallai の定理を満たすことができないので，この関数は偽を返します． その後，静的メソッド is_degree_sequence を用いて，入力シーケンスが次数シーケンスであるかどうか，つまり，シーケンスの要素が非増加であるかどうかをチェックします． 入力は次数列であることが前提なので、このチェックは余計なことですが、効率のためにやめても構いません。 さて、2番目のif文の本文で、定理の不等式が成立しているかどうかをチェックする。
余計な次数列のテストがないバージョン。
グラフ密度
グラフ密度とは、与えられたグラフの辺の数と、そのグラフが持ちうる辺の総数との比として定義される。 言い換えれば 与えられたグラフがどれだけ完全なグラフに近いかを測定する。
グラフが完全であれば、最大密度は1です。 これは、グラフの最大辺数は頂点に依存し、次のように計算できるからです：
最大辺数 = ½ * |V| * ( |V| – 1 ).
一方、グラフに辺がない場合、つまり孤立グラフの場合、最小密度は0である。
無向単純グラフの場合、グラフ密度は次のように定義される：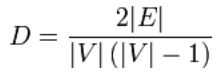
密なグラフとは、辺の数が最大辺の数に近いグラフのことである。 少数のエッジしかないグラフはスパースグラフと呼ばれる。 この2つの用語の定義はあまりシャープではなく、疎密グラフの定義には最小上界（supremum）、密グラフの定義には最大下界（infimum）がない。
最も正確な数学表記はビッグO表記を用いる。
密なグラフ(Dense Graph)。
密なグラフとは、グラフ G = (V, E) で、｜E｜ = Θ(|V|2) である。
「density」は、グラフの密度を計算するクラスのメソッドである：
def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))
このメソッドを次のスクリプトでテストすることができる。 先ほどのテストスクリプトの結果からわかるように、完全なグラフは密度が1、孤立したグラフは密度が0です：
$ python test_density.py 0.4666666666671.00.0
Connected Graphs
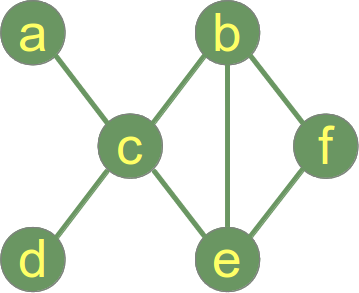グラフ内のすべての頂点のペアがつながっている場合、そのグラフは「つながっている」と言われます。 右側のグラフは連結グラフです。
グラフが連結しているかどうかは、簡単なアルゴリズムで判断できます：
- グラフGの任意のノードxを始点として選ぶ
- xから到達可能なすべてのノードの集合Aを求める。
- AがGのノードの集合と等しければグラフは連結、そうでなければ切断である。
グラフが連結グラフであるかどうかを調べるために、is_connectedメソッドを実装しています。 効率重視ではなく、読みやすさを重視しています。
このメソッドをグラフクラスに追加すると、以下のようなスクリプトでテストできます。 グラフクラスをgraph2.pyとして保存したと仮定して。
連結成分は G の最大連結部分グラフで、各頂点は各辺と同様にちょうど 1 つの連結成分に属します。
グラフの距離と直径
グラフ内の 2 点間の距離 “dist” は、これらの頂点間の最短経路の長さを指します。 距離の計算には、バックトラック、回り道、ループは許されない。
右のグラフの例では、頂点aと頂点fの距離は3、つまりdist(a,f)=3です。これは、頂点cとe（あるいはcとb）を経由するのが最短経路だからです。
グラフgの頂点sの離心率とは、グラフの他のすべての頂点との距離の最大値です。
e(s) = max( { dist(s,v) | v ∈ V })
(V はgの全頂点の集合)
グラフの直径dはグラフ中の任意の頂点の最大離心率として定義されます。 つまり、直径は最も距離のあるノード間の最短経路の長さである。 グラフの直径を求めるには、まず、各頂点の組の間の最短経路を求める。
この例のグラフでは、a-f間の最小の長さが3であり、これより長い経路を持つ頂点の組が他にないので、直径は3であることが直接わかる。
以下の方法は、直径を計算するアルゴリズムを実装したものである。 グラフクラスが graph2.py として保存されていると仮定して、次のスクリプトでグラフの直径を計算することができます。 これは、グラフの任意の2つの頂点がちょうど1つの単純なパスで接続されていることを意味します。
森は木の不連続な結合である。 自然界の森とは逆に、グラフ理論における森は1本の木からなることもある！
頂点が1つで辺がないグラフは木（と森）である：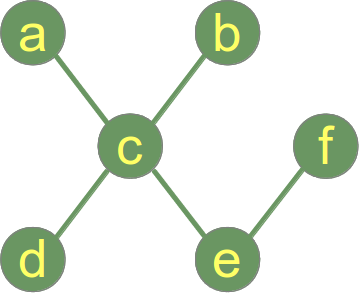
前の例が木と森であるグラフであるのに対し、次の図は2本の木からなるグラフ、つまり木と森であるグラフを表している。
forest の概要：
頂点が1つのもの：
頂点が2つのもの：Forest Graphs with two verices:
3つの頂点を持つフォレストグラフ：
3つの頂点を持つフォレストグラフ。
Spanning Tree
連結無向グラフGのspanning tree TはGの部分グラフG’で、これは木であり、G’にはGの全ての頂点と辺の部分集合が含まれます。 非公式には、Gの散布木は、すべての頂点にまたがる木を形成するGの辺の選択である。
例：
完全連結グラフ：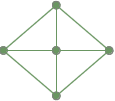
前の完全連結グラフから2つのスパニングツリーを作成する。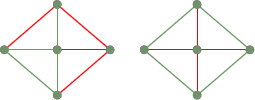
Hamiltonian Game
Hamiltonian path とは、無向グラフまたは有向グラフにおいて各頂点をちょうど一回訪れる経路のことである。 ハミルトンサイクル（またはサーキット）とは、ハミルトンパスがサイクルであることである。
コンピュータ科学者のためのノート。 ハミルトン経路問題はNP完全であることが証明されているので、一般に、任意のグラフにそのような経路やサイクルが存在するかどうかを決定することはできない。
この名前は、正十二面体の辺グラフにハミルトンサイクルを見出す、いわゆる「アイコシアンゲーム」（ハミルトンのパズル）を考案したウィリアム・ローワン・ハミルトンに因む。 ハミルトンはこの問題を、同じくハミルトンが発明した四元数（クォータニオン）と多くの類似点を持つ、単根に基づく代数的構造であるアイコシアン微積分を用いて解決した。
Graphクラスの完全なリスト
このGraphクラスを次のプログラムでテストすることができます。このプログラムを起動すると、次のような出力が得られます。
Footnotes:
1 グラフ理論（および Python チュートリアルのこの章）で学ぶグラフは、関数のグラフと混同しないでください
2 シングルトンは、正確に 1 つの要素を含むセットです。
Credits:
Narayana Chikkam, nchikkam(at)gmail(dot)com は “erdoes_gallai” 法におけるインデックス エラーを指摘しました。 Narayanaさん、どうもありがとうございました！
。