By Evan Ma

(Math and Physics tutor at The Edge Learning Center)

対数関数はIB Math SLプログラムを学ぶ多くの生徒を混乱させているようです。 正しく理解するために、

ここで、厳密に正の実数であるを底、をべき乗と呼んで定義しましょう。 例えば、

というように、誰もが心得ていることであろう。 対数関数はこれを逆にしたもので、引数として数値を与えると、指定された底に従うべき乗を求めるので、次のように定義されます。

If

then

したがって、

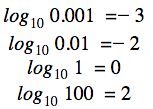
というように明らかになるわけである。 他の塩基を含む例を見てみましょう。

練習として次の問題を完成させましょう。 (a) , (b) , (c) , (d) . 答えは、このブログの最後にあります。

対数の定義から、実数の底対数で底を上げれば、数が戻ってくることもわかります。 viz

これを、計算機で有効基数を変えて検証してみるとよいでしょう。 この恒等式は、対数方程式を解くときに重要であり、その例題は後述します。 対数の定義と同様に、指数の法則を利用してルールを導き出します：

1. 積の対数は対数の和

Proof: 2960＞と＜5697＞を言う、よって＜7255＞＜9009＞2.Mrの底＜4668＞対数は＜9868＞×＜6611＞＜7255＞＜9009＞証明する。 2960＞と言うので＜7255＞＜9009＞＜1967＞mr-apr＜5060＞＜609＞3.商の対数は対数の差＜7255＞＜9009＞証明する。 2960＞と＜5697＞を言うから＜7255＞＜9009＞＜6254＞mn-apaq＜3645＞＜7255＞＜9009＞4. 最後の規則を基数変化公式と呼ぶ。 この公式を導き出す道具として、ある例を使うことにする。 例えば、2を何乗すれば50になるかを知りたいとする。 50は2の整数乗ではないので、答えはあまり明白ではない。 そこで、

と書くと、となる。 を求めるには、電卓に底2の対数キーがないので、式の両辺に底10の対数を適用すると、

有効数字4に補正して、 の値は約5.644になります。 実際、2を5.644の累乗にすると、答えが約50になることを確認することができます。

問題を一般化するために、となるを求めなければならず、base-対数が自由に使えない場合を考えてみましょう。 という式が成り立つので、

となり、

を例にすると、次のようになります。 万ドルを年利2.5％、年複利で預けたとする。 このお金を5万円に増やすには、どれくらいの期間、口座に置いておかなければならないか。

この問いに答えるには、基本的に

私の簡易科学計算機では1の底を指定できないので、nを求めることになる。7255>

利子は年複利なので、少なくとも5倍になるには66年かかります。

対数の規則を調べたところで、自然対数関数、つまり を紹介します。 ここでは著名な無理数≈2.71828で、その科学と数学における重要性はいくら強調してもし過ぎることはない。 7255>

If

then

次に、対数の方程式を解く上でよく間違えられる例を二つ見ておきましょう。 間違いがわかるかどうか見てみましょう。

間違いはどこでしょうか？ よく見てください。 もちろん、第2ステップでは、足し算の記号をはさんで対数を「分割」することはできません。 対数を和に「分割」できるのは、対数が和ではなく、積に適用される場合だけであることを覚えておいてください。

さて、次の例を見て、間違いがわかるかどうか見てみましょう：

間違いはどこでしょうか。 そうです、2番目のステップにあります。対数の商はもちろん商の対数ではありません。 7255>

最後に、対数の法則を使って次のように解く方法を説明します：

未知数は対数の引数に底と変数として現れることに気づくかもしれません。 どうすればを解くことができるのでしょうか。 この方法は、やはり対数のルールを一貫して適用することによります。 まず、両辺を底の累乗として上げると、

対数の定義で、左辺がちょうど対数の引数になることを思い出したかも知れませんね。 となるので、

上の式を並べ替えて、

これがの2次式に似ていることに着目し、を解くと次のようになります。

さて、負の根はどこにあるのでしょうか。 は対数の底でもあるので、負根は解として否定される。 よって、が最終的な答えとなります。

以上の例題を確認すると、一見難しそうに見える対数方程式を解くことは全く難しくなく、対数のルールを一貫して適用するだけで、正しい解が得られることがお分かりいただけるかと思います。 (a) 2 (b) 3 (c) -3 (d) -2.

。