Capítulo anterior: Python Network Scanner
Próximo Capítulo: Gráficos: PyGraph

Gráficos em Python

Origins of Graph Theory

Antes de começarmos com as implementações reais dos gráficos em Python e antes de começarmos com a introdução dos módulos Python que lidam com gráficos, queremos nos dedicar às origens da teoria dos gráficos.
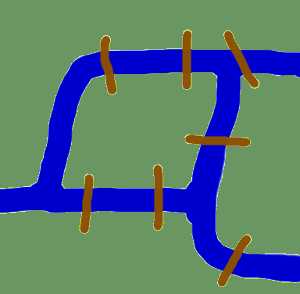
As origens nos levam de volta no tempo ao Künigsberg do século 18. Königsberg era uma cidade na Prússia daquela época. O rio Pregel correu através da cidade, criando duas ilhas. A cidade e as ilhas foram ligadas por sete pontes, como mostrado. Os habitantes da cidade foram movidos pela pergunta, se era possível dar um passeio pela cidade, visitando cada área da cidade e atravessando cada ponte apenas uma vez? Cada ponte deve ter sido completamente atravessada, ou seja, não é permitido caminhar a meio caminho de uma ponte e depois dar meia volta e mais tarde atravessar a outra metade a partir do outro lado. A caminhada não precisa começar e terminar no mesmo lugar. Leonhard Euler resolveu o problema em 1735, provando que não é possível. Ele descobriu que a escolha de uma rota dentro de cada área terrestre é irrelevante e que a única coisa que importava era a ordem (ou a sequência) em que as pontes eram atravessadas. Ele havia formulado uma abstração do problema, eliminando fatos desnecessários e focalizando as áreas de terra e as pontes que as ligam. Desta forma, ele criou os fundamentos da teoria dos gráficos. Se vemos uma “área terrestre” como um vértice e cada ponte como uma borda, temos “reduzido” o problema a um gráfico.

Introdução em Teoria dos Gráficos Usando Python

Antes de começarmos nosso tratado sobre possíveis representações Python de gráficos, queremos apresentar algumas definições gerais de gráficos e seus componentes.
Um “gráfico “1 em matemática e informática consiste em “nós”, também conhecidos como “vértices”.Os nós podem ou não estar conectados uns aos outros. Na nossa ilustração, – que é uma representação pictórica de um gráfico, – o nó “a” está conectado com o nó “c”, mas “a” não está conectado com “b”. A linha de conexão entre dois nós é chamada de borda. Se as bordas entre os nós não estiverem direcionadas, o gráfico é chamado de gráfico não direcionado. Se uma borda é direcionada de um vértice (nó) para outro, um gráfico é chamado de gráfico direcionado. Uma aresta direcionada é chamada de arc.
Graphics bastante teóricos, muitos problemas práticos podem ser representados por gráficos. Eles são frequentemente usados para modelar problemas ou situações em física, biologia, psicologia e acima de tudo em ciência da computação. Na informática, os gráficos são usados para representar redes de comunicação, organização de dados, dispositivos computacionais, o fluxo de computação,
Neste último caso, os gráficos são usados para representar a organização de dados, como o sistema de arquivos de um sistema operacional, ou redes de comunicação. A estrutura de links de websites também pode ser vista como um gráfico, ou seja, um gráfico dirigido, porque um link é uma borda dirigida ou um arco,
Python não tem tipo de dados ou classe incorporada para gráficos, mas é fácil de implementá-los em Python. Um tipo de dado é ideal para representar gráficos em Python, ou seja, dicionários. O gráfico em nossa ilustração pode ser implementado da seguinte forma:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

As chaves do dicionário acima são os nós do nosso gráfico. Os valores correspondentes são listas com os nós, que estão conectados por uma borda. Não há uma maneira mais simples e elegante de representar um gráfico.
Uma borda pode ser vista como um 2-tuplo com nós como elementos, ou seja (“a”, “b”)
Função para gerar a lista de todas as arestas:Este código gera a seguinte saída, se combinado com o dicionário do gráfico previamente definido:

 $ python3 graph_simple.py 

Como podemos ver, não há borda contendo o nó “f”. “f” é um nó isolado do nosso gráfico.
A seguinte função Python calcula os nós isolados de um dado gráfico:Se chamarmos esta função com nosso gráfico, uma lista contendo “f” será retornada:

Gráficos como uma classe Python

Antes de continuarmos com as funções de escrita de gráficos, temos uma primeira vez a implementação de uma classe de gráficos Python. Se você olhar para a seguinte listagem da nossa classe, você pode ver no método __init__ que nós usamos um dicionário “self.__graph_dict” para armazenar os vértices e seus correspondentes vértices adjacentes.
Se você iniciar este módulo de forma autônoma, você obterá o seguinte resultado:

Caminhos nos Gráficos

Queremos encontrar agora o caminho mais curto de um nó para outro nó. Antes de chegarmos ao código Python para este problema, teremos que apresentar algumas definições formais.
Vértices adjacentes:
Dois vértices são adjacentes quando ambos são incidentes a uma borda comum.
Caminho em um gráfico não direcionado:
Um caminho em um gráfico não direcionado é uma seqüência de vértices P = ( v1, v2, …., vn ) ∈ V x V x … x V tal que vi é adjacente a v{i+1} para 1 ≤ i < n. Tal caminho P é chamado de caminho de comprimento n de v1 a vn.
Caminho simples:
Um caminho sem vértices repetidos é chamado de caminho simples.
Exemplo:
(a, c, e) é um caminho simples em nosso gráfico, assim como (a,c,e,b). (a,c,e,b,c,d) é um caminho mas não um caminho simples, porque o nó c aparece duas vezes.
O método seguinte encontra um caminho desde um vértice inicial até um vértice final:Se salvarmos nossa classe gráfica incluindo o método find_path como “graphs.py”, podemos verificar a forma de trabalho da nossa função find_path:O resultado do programa anterior se parece com isto:
O método find_all_paths encontra todos os caminhos entre um vértice inicial e um vértice final:Mudamos ligeiramente nosso gráfico de exemplo adicionando bordas de “a” para “f” e de “f” para “d” para testar o método previamente definido:O resultado se parece com isto:

grau

O grau de um vértice v em um gráfico é o número de arestas conectando-o, com loops contados duas vezes. O grau de um vértice v é denotado deg(v). O grau máximo de um gráfico G, denotado por Δ(G), e o grau mínimo de um gráfico, denotado por δ(G), são o grau máximo e mínimo dos seus vértices.
No gráfico do lado direito, o grau máximo é 5 no vértice c e o grau mínimo é 0, ou seja, o vértice isolado f.
Se todos os graus de um gráfico são iguais, o gráfico é um gráfico regular. Num gráfico regular, todos os graus são iguais, e assim podemos falar do grau do gráfico.
A fórmula da soma dos graus (Handshaking lemma):
∑v &in; Vdeg(v) = 2 |E|
Isto significa que a soma dos graus de todos os vértices é igual ao número de arestas multiplicado por 2.Podemos concluir que o número de vértices com grau ímpar tem que ser par. Esta afirmação é conhecida como o lema do aperto de mão. O nome “lema do aperto de mão” deriva de um problema matemático popular: Em qualquer grupo de pessoas o número de pessoas que apertaram a mão com um número ímpar de outras pessoas do grupo é par.
O método seguinte calcula o grau de um vértice:
O método seguinte calcula uma lista contendo os vértices isolados de um gráfico:Os métodos delta e Delta podem ser usados para calcular o grau mínimo e máximo de um vértice respectivamente:

Sequência de graus

A sequência de graus de um gráfico não dirigido é definida como a sequência dos seus vértices numa ordem não crescente.
O método seguinte retorna um tuple com a sequência de graus do gráfico de instância:
A sequência do grau do nosso gráfico de exemplo é a seguinte sequência de números inteiros: (5,2,1,1,1,0).
Os gráficos isomórficos têm a mesma sequência de graus. Contudo, dois gráficos com a mesma sequência de graus não são necessariamente isomórficos.
Existe a questão se uma dada sequência de graus pode ser realizada por um gráfico asimples. O teorema de Erdös-Gallai afirma que uma sequência não crescente de n números di (fori = 1, …n) é a seqüência de graus de um gráfico simples se e somente se a soma da seqüência for igual e a seguinte condição for cumprida:

Aplicação do teorema de Erdös-Gallai

Nossa classe de gráficos – veja mais abaixo para uma lista completa – contém um método “erdoes_gallai” que decide, se uma seqüência cumpre o teorema de Erdös-Gallai. Primeiro, verificamos, se a soma dos elementos da sequência é estranha. Se sim, a função retorna Falso, porque o teorema de Erdös-Gallai não pode mais ser cumprido. Depois disso, verificamos com o método estático is_degree_sequence se a sequência de entrada é uma sequência de graus, ou seja, se os elementos da sequência não estão a aumentar. Isto é um pouco supérfluo, pois a entrada é suposta ser uma sequência de graus, então você pode deixar esta verificação para eficiência. Agora, verificamos no corpo do segundo se a afirmação, se a inequação do teorema é cumprida:
Versão sem o teste de sequência de graus supérfluos:

Densidade do gráfico

A densidade do gráfico é definida como a razão entre o número de arestas de um dado gráfico, e o número total de arestas, que o gráfico poderia ter. Em outras palavras: Mede o quão próximo um dado gráfico está de um gráfico completo.
A densidade máxima é 1, se um gráfico estiver completo. Isto é claro, porque o número máximo de arestas em um gráfico depende dos vértices e pode ser calculado como:
max. número de arestas = ½ * | V| * ( | V| – 1 ).
Por outro lado a densidade mínima é 0, se o gráfico não tiver arestas, ou seja, é um gráfico isolado.
Para gráficos simples não direcionados, a densidade do gráfico é definida como: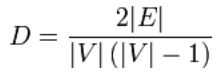

Um gráfico denso é um gráfico em que o número de arestas está próximo do número máximo de arestas. Um gráfico com apenas algumas arestas, é chamado de gráfico esparso. A definição para esses dois termos não é muito acentuada, ou seja, não há limite inferior (supremum) para uma densidade esparsa e nenhum limite inferior maior (infimum) para definir um gráfico denso.
A notação matemática mais precisa usa a grande notação O:
Gráfico Esparso:
Gráfico denso:
Um gráfico denso é um gráfico G = (V, E) no qual |E| = Θ(|V|2).
“densidade” é um método da nossa classe para calcular a densidade de um gráfico:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Podemos testar este método com o seguinte script. Um gráfico completo tem uma densidade de 1 e um gráfico isolado tem uma densidade de 0, como podemos ver nos resultados do script de teste anterior:

$ python test_density.py 0.4666666666671.00.0

Gráficos conectados

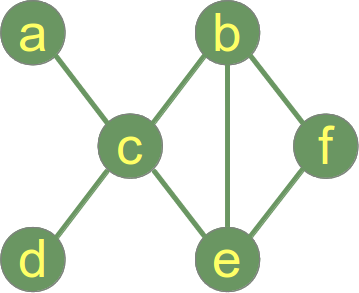Diz-se que um gráfico está conectado se cada par de vértices do gráfico estiver conectado. O gráfico de exemplo no lado direito é um gráfico conectado.
É possível determinar com um algoritmo simples se um gráfico está conectado:

1. Selecionar um nó x arbitrário do gráfico G como ponto de partida
2. Determinar o conjunto A de todos os nós que podem ser alcançados a partir de x.
3. Se A for igual ao conjunto de nós de G, o gráfico é conectado; caso contrário é desconectado.

Implementamos um método is_connected para verificar se um gráfico é um gráfico conectado. Nós não colocamos ênfase na eficiência, mas na legibilidade.
Se você adicionar este método à nossa classe de gráfico, podemos testá-lo com o seguinte script. Assumindo que você salve a classe do gráfico como graph2.py:
Um componente conectado é um subgrafo máximo conectado de G. Cada vértice pertence exatamente a um componente conectado, assim como cada borda.

Distância e Diâmetro de um Gráfico

A distância “dist” entre dois vértices de um gráfico é o comprimento do caminho mais curto entre esses vértices. Não são permitidos retrocessos, desvios ou loops para o cálculo de uma distância.
No nosso gráfico de exemplo à direita, a distância entre o vértice a e o vértice f é 3, ou seja, dist(a,f) = 3, porque o caminho mais curto é através dos vértices c e e (ou c e b em alternativa).
A excentricidade de um vértice s de um gráfico g é a distância máxima a cada outro vértice do gráfico:
e(s) = max( { dist(s,v) | v ∈ V })
(V é o conjunto de todos os vértices de g)
O diâmetro d de um gráfico é definido como a excentricidade máxima de qualquer vértice do gráfico. Isto significa que o diâmetro é o comprimento do caminho mais curto entre os nós mais distanciados. Para determinar o diâmetro de um gráfico, primeiro encontre o caminho mais curto entre cada par de vértices. O maior comprimento de qualquer um desses caminhos é o diâmetro do gráfico.
No nosso gráfico de exemplo podemos ver diretamente que o diâmetro é 3, porque o comprimento mínimo entre a e f é 3 e não há outro par de vértices com um caminho mais longo.
O método seguinte implementa um algoritmo para calcular o diâmetro. Podemos calcular o diâmetro do nosso gráfico de exemplo com o seguinte script, assumindo novamente, que a nossa classe gráfica completa é salva como graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Imprimirá o valor 3.

A classe gráfica Python completa

No seguinte código Python, você encontra o módulo completo da classe Python com todos os métodos discutidos:graph2.py

Árvore / Floresta

Uma árvore é um gráfico não direcionado que não contém ciclos. Isto significa que quaisquer dois vértices do gráfico estão conectados por exatamente um caminho simples.
Uma floresta é uma união desarticulada de árvores. Ao contrário das florestas na natureza, uma floresta na teoria dos gráficos pode consistir de uma única árvore!
Um gráfico com um vértice e nenhuma borda é uma árvore (e uma floresta).
Um exemplo de uma árvore: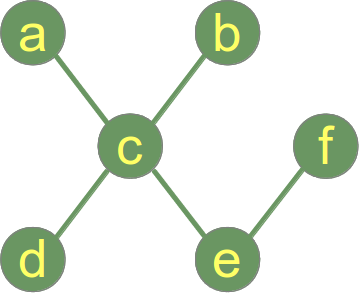

Apesar do exemplo anterior descrever um gráfico que é uma árvore e uma floresta, a figura seguinte mostra um gráfico que consiste de duas árvores, i.e. o gráfico é uma floresta mas não uma árvore:

Vista geral das florestas:

Com um vértice:
>
Gráficos florestais com dois vértices:

Gráficos florestais com três vértices:

Árvore espaçadora

Uma árvore espaçadora T de um gráfico G conectado, não direcionado, é um subgráfico G’ de G, que é uma árvore, e G’ contém todos os vértices e um subconjunto das bordas de G. G’ contém todas as bordas de G, se G for um gráfico em árvore. Informalmente, uma árvore de G é uma seleção de arestas de G que formam uma árvore que abrange todos os vértices. Ou seja, cada vértice está na árvore, mas nenhum ciclo (ou loop) está contido.
Exemplo:
Um gráfico totalmente conectado: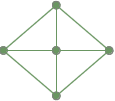

Duas árvores spanning do gráfico anterior totalmente conectado: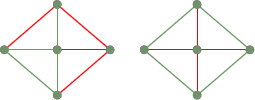

Jogo Hamiltoniano

Um caminho Hamiltoniano é um caminho em um gráfico não direcionado ou direcionado que visita cada vértice exatamente uma vez. Um ciclo (ou circuito) Hamiltoniano é um caminho Hamiltoniano que é um ciclo.
Nota para cientistas da computação: Geralmente não é possível determinar, se tais caminhos ou ciclos existem em gráficos arbitrários, porque o problema do caminho Hamiltoniano foi provado ser NP-complete.
É nomeado em homenagem a William Rowan Hamilton que inventou o chamado “jogo icosiano”, ou quebra-cabeça Hamiltoniano, que envolve encontrar um ciclo Hamiltoniano no gráfico de borda do dodecaedro. Hamilton resolveu este problema usando o cálculo icosiano, uma estrutura algébrica baseada em raízes de unidade com muitas semelhanças com os quaterniões, que ele também inventou.

Listagem Completa da Classe de Gráfico

Podemos testar esta classe de Gráfico com o seguinte programa:Se iniciarmos este programa, obtemos a seguinte saída:
Notas de pés:
1 Os gráficos estudados na teoria dos gráficos (e neste capítulo do nosso tutorial Python) não devem ser confundidos com os gráficos de funções
2 Um singleton é um conjunto que contém exatamente um elemento.
Créditos:
Narayana Chikkam, nchikkam(at)gmail(dot)com, apontou um erro de índice no método “erdoes_gallai”. Muito obrigado, Narayana!