No capítulo anterior, discutimos sobre Latches. Esses são os blocos básicos de construção dos chinelos de dedo. Podemos implementar os flip-flops em dois métodos.
No primeiro método, em cascata duas travas de tal forma que a primeira trava é habilitada para cada pulso de relógio positivo e a segunda trava é habilitada para cada pulso de relógio negativo. Para que a combinação destas duas travas se torne um flip-flop.
No segundo método, podemos implementar diretamente o flip-flop, que é sensível à borda. Neste capítulo, vamos discutir os seguintes flip-flops usando o segundo método.
- SR Flip-Flop
- D Flip-Flop
- JK Flip-Flop
- T Flip-Flop
SR Flip-Flop
SR Flip-flop opera apenas com transições positivas do relógio ou negativas do relógio. Já o trinco SR funciona com o sinal de ativação. O diagrama de circuito do flip-flop SR é mostrado na figura seguinte.
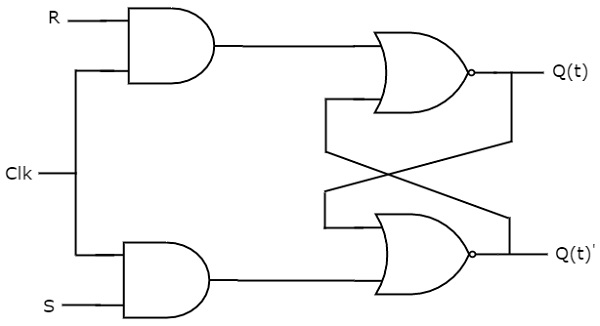
Este circuito tem duas entradas S & R e duas saídas Q(t) & Q(t)’. O funcionamento do Flip-Flop SR é similar ao Latch SR. Mas, este flip-flop afeta as saídas somente quando a transição positiva do sinal do relógio é aplicada ao invés da ativação.
A tabela seguinte mostra a tabela de estados do flip-flop do SR.
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | – |
Aqui, Q(t) & Q(t + 1) são estado presente & estado seguinte, respectivamente. Assim, a inversão do SR pode ser usada para uma destas três funções, como Hold, Reset & Set baseado nas condições de entrada, quando a transição positiva do sinal do relógio é aplicada. A tabela seguinte mostra a tabela de características do flip-flop do SR.
| Entradas Presentes | ||||
|---|---|---|---|---|
| S | R | Q(t) | Q(t + 1) | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | x | |
| 1 | 1 | 1 | 1 | x |
Usando três variáveis K-Mapa, podemos obter a expressão simplificada para o próximo estado, Q(t + 1). As três variáveis K-Map para o próximo estado, Q(t + 1) é mostrada na figura seguinte.
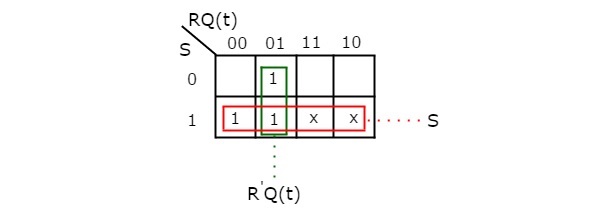
Os agrupamentos máximos possíveis de agrupamentos adjacentes já são mostrados na figura. Portanto, a expressão simplificada para o próximo estado Q(t + 1) é
$Q\esquerda ( t+1 \direita )=S+{R}’Q\esquerda ( t \direita )$
D Flip-Flop
D flip-flop opera apenas com transições de relógio positivas ou negativas. Já o trinco D funciona com o sinal de ativação. Isso significa que a saída do D flip-flop é insensível às mudanças na entrada, D exceto para a transição ativa do sinal do relógio. O diagrama do circuito do D flip-flop é mostrado na figura seguinte.
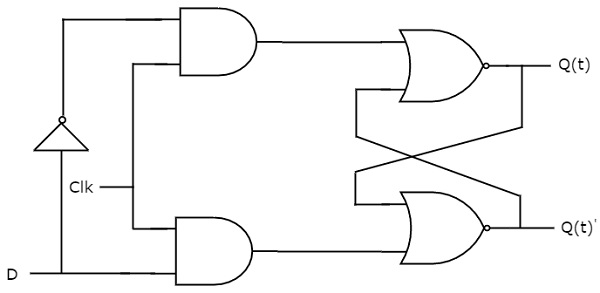
Este circuito tem uma entrada D e duas saídas Q(t) & Q(t)’. O funcionamento do D flip-flop é similar ao D Latch. Mas, este flip-flop afeta as saídas somente quando a transição positiva do sinal do relógio é aplicada ao invés da habilitação ativa.
A tabela seguinte mostra a tabela de estados do D flip-flop.
>
| D | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Por isso, D flip-flop Manter sempre a informação, que está disponível na entrada de dados, D de transição positiva anterior do sinal do relógio. Da tabela de estados acima, podemos escrever diretamente a equação de estado seguinte como
Q(t + 1) = D
Nexterior estado de D flip-flop é sempre igual à entrada de dados, D para cada transição positiva do sinal do relógio. Portanto, D flip-flops pode ser usado em registros, registros de deslocamento e alguns dos contadores.
JK Flip-Flop
JK flip-flop é a versão modificada do SR flip-flop. Ele opera apenas com transições positivas ou negativas do relógio. O diagrama do circuito de JK flip-flop é mostrado na figura seguinte.
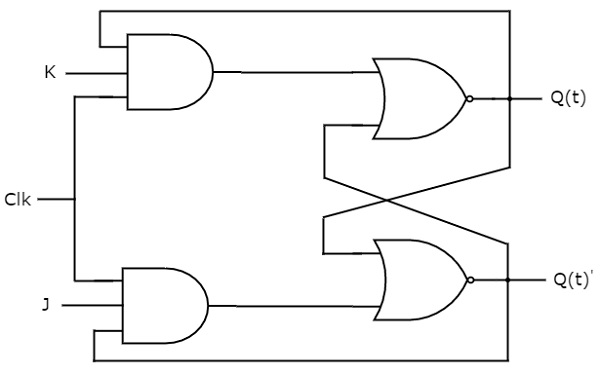
Este circuito tem duas entradas J & K e duas saídas Q(t) & Q(t)’. O funcionamento do JK flip-flop é similar ao do SR flip-flop. Aqui, consideramos as entradas do flip-flop SR como S = J Q(t)’ e R = KQ(t)’ para utilizar o flip-flop SR modificado para 4 combinações de entradas.
A tabela seguinte mostra a tabela de estados do flip-flop JK.
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q(t)’ |
Aqui, Q(t) & Q(t + 1) são estado presente & estado seguinte, respectivamente. Assim, JK flip-flop pode ser usado para uma destas quatro funções como Hold, Reset, Set & Complemento do estado presente baseado nas condições de entrada, quando a transição positiva do sinal do relógio é aplicada. A tabela a seguir mostra a tabela característica de JK flip-flop.
| Entradas presentes | ||||
|---|---|---|---|---|
| J | K | Q(t) | Q(t+1) | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 0 |
Usando três variáveis K-Mapa, podemos obter a expressão simplificada para o próximo estado, Q(t + 1). Três variáveis K-Map para o próximo estado, Q(t + 1) é mostrada na figura seguinte.
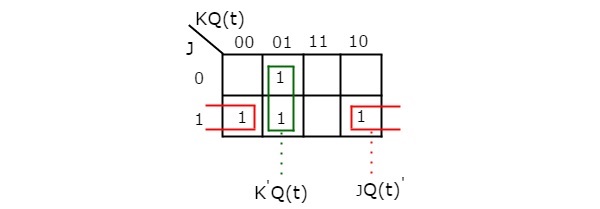
Os agrupamentos máximos possíveis de agrupamentos adjacentes já são mostrados na figura. Portanto, a expressão simplificada para o próximo estado Q(t+1) é
$$Q\esquerda ( t+1 \direita )=J{Q\esquerda ( t \direita )}’+{K}’Q\esquerda ( t \direita )$$
T Flip-Flop
T flip-flop é a versão simplificada de JK flip-flop. Ele é obtido conectando a mesma entrada ‘T’ às duas entradas do JK flip-flop. Ele opera apenas com transições de relógio positivas ou negativas. O diagrama de circuito do T flip-flop é mostrado na figura seguinte.
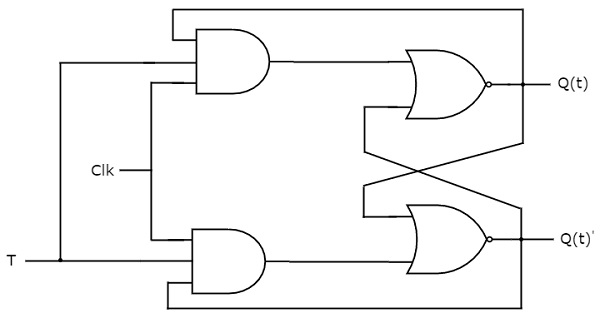
Este circuito tem uma entrada T e duas saídas Q(t) & Q(t)’. O funcionamento do T flip-flop é o mesmo que o do JK flip-flop. Aqui, consideramos as entradas de JK flip-flop como J = T e K = T para utilizar o JK flip-flop modificado para 2 combinações de entradas. Assim, eliminamos as outras duas combinações de J & K, para as quais esses dois valores são complementares entre si em T flip-flop.
A tabela seguinte mostra a tabela de estados do T flip-flop.
| D | Q(t + 1) |
|---|---|
| 0 | Q(t) |
| 1 | Q(t)’ |
Aqui, Q(t) & Q(t + 1) são estado presente & estado seguinte, respectivamente. Assim, T flip-flop pode ser usado para uma destas duas funções como Hold, & Complemento do estado presente baseado nas condições de entrada, quando a transição positiva do sinal do relógio é aplicada. A tabela a seguir mostra a tabela característica do T flip-flop.
| Entradas | |||
|---|---|---|---|
| T | Q(t) | Q(t + 1) | |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Da tabela de características acima, podemos escrever diretamente a próxima equação de estado como
$$Q\esquerda ( t+1 \direita )={T}’Q\esquerda ( t \direita )+TQ{\esquerda ( t \direita )}’$$
$$$$$$$Squerda Q\esquerda ( t+1 \direita )=T+ Q\esquerda ( t \direita )$$
A saída do T flip-sempre alternância para cada transição positiva do sinal do relógio, quando a entrada T permanece na lógica Alta (1). Assim, T flip-flop pode ser usado em contadores.
Neste capítulo, implementamos vários flip-flops fornecendo o acoplamento cruzado entre os portões NOR. Da mesma forma, você pode implementar estes chinelos de dedo usando portas NAND.