No início, geralmente é necessário ter a idéia do diagrama pV do ciclo. Para isso vamos traçar as curvas dos processos isocórico e adiabático. O gráfico aproximado do ciclo Otto é mostrado na figura seguinte.
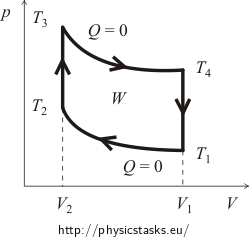
A eficiência η do ciclo é definida como
\
onde W é o trabalho realizado pelo gás durante um ciclo menos o trabalho realizado pelas forças externas (no diagrama é representado pela superfície da área definida pelas linhas do ciclo!) e Qsup é o calor fornecido ao sistema durante o ciclo.
O trabalho W pode ser calculado utilizando a relação entre a pressão e o volume durante uma expansão e compressão adiabáticas (o trabalho realizado durante um processo isocórico é, naturalmente, zero). Nesta tarefa, porém, será melhor usar o fato de que a variação total da energia interna por ciclo deve ser igual a zero (voltamos ao mesmo estado que no início, portanto a temperatura e, portanto, a energia interna permanece a mesma!) Segundo a Primeira Lei da Termodinâmica, o trabalho realizado pelo gás pode ser expresso como a diferença entre o Qsup de calor fornecido e o Qrel de calor liberado. A fórmula para a eficiência do ciclo é portanto na forma de
\
Primeiro, vamos calcular o Qsup de calor fornecido. É claro que durante o processo adiabático não há troca de calor e durante o resfriamento isocórico o calor é liberado. Isto significa que o calor será fornecido apenas durante o aquecimento isocórico desde a temperatura T2 até a temperatura T3. A quantidade deste calor pode ser expressa nas variáveis da quantidade de substância n do gás e sua capacidade de calor molar CV da seguinte forma:
\
Expressaremos a quantidade de calor liberada Qrel de forma muito semelhante. Já sabemos que o calor é liberado somente durante o resfriamento isocórico, desde a temperatura T4 até a temperatura inicial T1. É verdade que:
\
Agora substituímos estas fórmulas na fórmula da eficiência do ciclo e imediatamente obtemos:
\
Agora precisaremos expressar as diferenças de temperatura usando a razão de compressão dada
\
e a razão de Poisson κ.
Para isso, usaremos a equação para um gás ideal submetido a um processo adiabático (a lei de Poisson) pVκ = C = konst.., onde C é uma constante. Agora avaliamos a pressão da equação de estado de um gás ideal
\
que substituímos na lei de Poisson. Agora transferimos as constantes (C e K) para um lado
\
Agora aplicamos esta lei de Poisson para ambos os processos adiabáticos. Para a expansão adiabática obtemos a relação
\
E para a compressão adiabática obtemos
\
Agora subtraímos a segunda equação da primeira e fatorizamos V1κ – 1 de um lado e V2κ – 1 do outro. Obtemos:
\
Vemos que de facto conseguimos expressar as diferenças de temperatura usando os valores dados. Agora substituímos esta relação na fórmula da eficiência e obtemos a equação final:
{\i1}-