Por Evan Ma

(Professor de Matemática e Física no The Edge Learning Center)

A função logarítmica parece confundir muitos alunos que estudam o programa IB Math SL. Para entendê-lo corretamente, vamos definir

onde , um número real estritamente positivo, é chamado de base e é a potência. Por exemplo, todos sabemos de cor:

e assim por diante. A função logarítmica faz isso ao contrário – dado um número como argumento, ela produz a potência sujeita a uma base especificada, e portanto é definida da seguinte forma.

Se

então

Por isso, é claro que

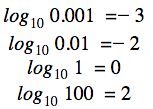
e assim por diante. Vejamos outros exemplos que envolvem outras bases:

Vamos completar as seguintes perguntas como prática: (a) , (b) , (c) , (d) . As respostas podem ser encontradas no final deste blog.

Da definição de logaritmo, também podemos ver que se levantarmos a base pela baselogaritmo de um número real , recuperaremos o número , viz

Pode tentar verificar isto usando a sua calculadora para diferentes bases válidas. Esta identidade é importante quando tentamos resolver equações logarítmicas, cujos exemplos serão dados alter.

Agora, vamos dar uma olhada nas regras do logaritmo. Similar à definição do logaritmo, nós usamos as leis dos índices para derivar as regras:

1. O logaritmo de um produto é a soma dos logaritmos

Proof: Digamos e , portanto

2. Base logaritmo do Sr é vezes

Prova: Digamos , portanto

3. Logaritmo de um quociente é a diferença de logaritmos

Prova: Digamos e , portanto

4. A regra final é chamada de fórmula da mudança de base. Vamos usar um exemplo como ferramenta para derivar a fórmula. Digamos que queremos saber que potência 2 deve ser aumentada para se obter 50. Como 50 não é uma potência inteira de 2, a resposta não é muito óbvia. Portanto, escrevemos

e portanto. Para encontrar , digamos que aplicamos o logaritmo base-10 a ambos os lados da equação, pois nossa calculadora pode não ter a chave logarítmica base-2:

Corrigido para 4 números significativos, o valor de é aproximadamente 5,644. Na verdade, você pode verificar sua resposta elevando 2 para a potência de 5,644 para ver que a resposta é de aproximadamente 50.

Para generalizar o problema, digamos que temos de encontrar tal que e base- logaritmo não está à nossa disposição, podemos, portanto, usar base- logaritmo de acordo com a equação

e portanto

A título de exemplo, vamos considerar o seguinte. Suponha que uma quantia de $10.000 seja depositada a um juro de 2,5% ao ano, composto anualmente. Por quanto tempo o dinheiro deve ser mantido na conta para que ele cresça até $50.000?

Para responder à pergunta, estamos basicamente tentando encontrar n tal que

Como minha simples calculadora científica não me permite especificar uma base de 1.025 para a chave logarítmica, terei que confiar na fórmula da mudança de base e usar a base 10, e portanto

Posto que o interesse é composto anualmente, levará 66 anos para crescer pelo menos 5 vezes.

Servindo regras exploradas de logaritmos, introduzimos a função logarítmica natural, ou . É a base –, onde é o número eminente irracional ≈2.71828 e cujo significado em ciências e matemática não pode ser enfatizado o suficiente. Assim, o base-logaritmo é definido da seguinte forma.

Se

then

Next, vejamos dois exemplos onde erros comuns são cometidos na resolução de equações de logaritmos. Veja se você pode identificar o erro.

Onde está o erro? Veja mais de perto. Claro que, no segundo passo, não se pode “dividir” o logaritmo através do sinal de adição. Lembre-se, você só pode “dividir” um logaritmo em uma soma se o logaritmo for aplicado a um produto, não a uma soma. Os passos corretos são, portanto, os seguintes:

Agora, vejamos o seguinte exemplo, e vejamos se você pode identificar o erro:

Onde está o erro? Sim, está no segundo passo – um quociente de logaritmos não é, naturalmente, o logaritmo do quociente. Pelo contrário, podemos usar a fórmula da mudança de base para simplificar o primeiro passo, como se segue:

Finalmente, vamos ilustrar como usar regras de logaritmo para resolver o seguinte:

Você pode notar que o desconhecido aparece como a base e uma variável no argumento do logaritmo. Como podemos resolver para ? O método ainda depende da aplicação das regras do logaritmo de forma consistente. Primeiro, levantamos ambos os lados como potências da base , e assim

Você pode lembrar da definição de logaritmo que o lado esquerdo se tornará apenas o argumento do logaritmo, e portanto

Ao reorganizar a equação acima, precisamos resolver

Notificando que isto se assemelha a um quadrático em , resolvemos para da seguinte forma

Agora, onde está a raiz negativa? Como é também a base do logaritmo, a raiz negativa é, portanto, rejeitada como solução. Portanto, é a resposta final.

Ao rever os exemplos acima, você pode ver que resolver uma equação logarítmica aparentemente difícil não é nada difícil – simplesmente aplique as regras do logaritmo de forma consistente e a solução correta pode ser obtida.

Respostas a perguntas: (a) 2 (b) 3 (c) -3 (d) -2.