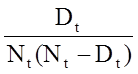Existem várias formas diferentes de estimar uma função de sobrevivência ou uma curva de sobrevivência. Existem vários métodos paramétricos populares que são usados para modelar dados de sobrevivência, e diferem em termos das suposições que são feitas sobre a distribuição dos tempos de sobrevivência na população. Algumas distribuições populares incluem as distribuições exponencial, Weibull, Gompertz e log-normal.2 Talvez a mais popular seja a distribuição exponencial, que assume que a probabilidade de um participante sofrer o evento de interesse é independente de há quanto tempo essa pessoa está livre de eventos. Outras distribuições fazem suposições diferentes sobre a probabilidade de um indivíduo desenvolver um evento (ou seja, pode aumentar, diminuir ou mudar com o tempo). Mais detalhes sobre métodos paramétricos para análise de sobrevivência podem ser encontrados em Hosmer e Lemeshow e Lee e Wang1,3.

Focamos aqui em dois métodos não paramétricos, que não fazem suposições sobre como a probabilidade de uma pessoa desenvolver o evento muda ao longo do tempo. Usando métodos não paramétricos, nós estimamos e plotamos a distribuição de sobrevivência ou a curva de sobrevivência. As curvas de sobrevivência são frequentemente traçadas como funções de passo, como mostrado na figura abaixo. O tempo é mostrado no eixo X e a sobrevivência (proporção de pessoas em risco) é mostrada no eixo Y. Note que a porcentagem de participantes sobreviventes nem sempre representa a porcentagem que está viva (o que pressupõe que o resultado de interesse é a morte). “Sobrevivência” também pode se referir à proporção que está livre de outro evento de resultado (por exemplo, porcentagem livre de IM ou doença cardiovascular), ou também pode representar a porcentagem que não experimenta um resultado saudável (por exemplo, remissão de câncer).

Função de Sobrevivência

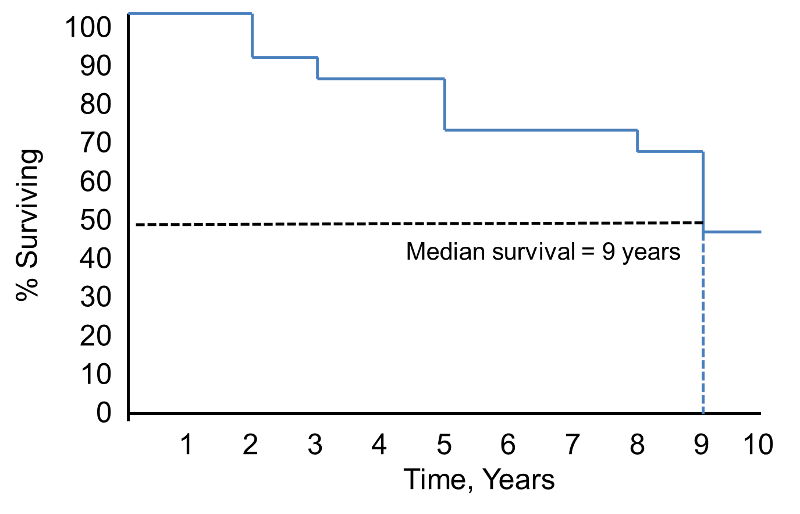
Nota que a probabilidade de sobrevivência é de 100% durante 2 anos e depois cai para 90%. A mediana de sobrevivência é de 9 anos (ou seja, 50% da população sobrevive 9 anos; ver linhas tracejadas).

Exemplo:

Considerar um pequeno estudo de coorte prospectivo projetado para estudar o tempo até a morte. O estudo envolve 20 participantes com 65 anos de idade ou mais; eles estão matriculados por um período de 5 anos e são acompanhados por até 24 anos até a morte, o estudo termina, ou eles desistem do estudo (perdidos para acompanhamento). Os dados são mostrados abaixo. No estudo, há 6 mortes e 3 participantes com acompanhamento completo (ou seja, 24 anos). Os 11 restantes têm menos de 24 anos de acompanhamento devido à inscrição tardia ou à perda de acompanhamento.

Número de Identificação do Participante	Ano da Morte	Ano do Último Contacto
>1	>	> 24
2	3
3		11
4		19
5		24
6		13
7	14
8		2
9		18
10		17
11		24
12		21
13		12
14	1
15		10
16	23
17		6
18	5
19		>9
>20	> 17	>

Tabela de Vida (Tabela Actuarial)

Uma forma de resumir as experiências dos participantes é com uma tábua de vida, ou uma tábua atuarial. As tábuas de vida são frequentemente usadas no setor de seguros para estimar a expectativa de vida e para definir os prêmios. Nós nos concentramos em um tipo particular de tábua de vida usada amplamente na análise bioestatística chamada tábua de vida de coorte ou uma tábua de vida de acompanhamento. A tábua de vida de acompanhamento resume as experiências dos participantes durante um período de acompanhamento predefinido em um estudo de coorte ou em um ensaio clínico até o momento do evento de interesse ou o final do estudo, o que ocorrer primeiro.

Para construir uma tábua de vida, primeiro organizamos os tempos de acompanhamento em intervalos igualmente espaçados. Na tabela acima temos um seguimento máximo de 24 anos, e consideramos intervalos de 5 anos (0-4, 5-9, 10-14, 15-19 e 20-24 anos). Somamos o número de participantes que estão vivos no início de cada intervalo, o número que morre e o número que é censurado em cada intervalo.

Intervalo em anos	Número Vivo no Início do Intervalo	Número de Mortes Durante o Intervalo	Número Censurado
0-4	20	2	1
5-9	17	1	2
10-14	14	1	4
15-19	9	1	3
20-24	>5	>1	4

Usamos a seguinte notação na nossa análise da tábua de mortalidade. Primeiro definimos a notação e depois a usamos para construir a tábua de mortalidade.

• Nt = número de participantes que estão livres de eventos e considerados em risco durante o intervalo t (por exemplo, neste exemplo o número vivo como nosso resultado de interesse é a morte)
• Dt = número de participantes que morrem (ou sofrem o evento de interesse) durante o intervalo t
• Ct = número de participantes que são censurados durante o intervalo t Nt* = número médio de participantes em risco durante o intervalo t
• Nt* = número médio de participantes em risco durante o intervalo t [Na construção das tábuas de vida actuariais, as seguintes suposições são frequentemente feitas: Primeiro, assume-se que os eventos de interesse (por exemplo, mortes) ocorrem no final do intervalo e assume-se que os eventos censurados ocorrem uniformemente (ou uniformemente) ao longo do intervalo. Portanto, muitas vezes é feito um ajuste para Nt para refletir o número médio de participantes em risco durante o intervalo, Nt*, que é calculado da seguinte forma: Nt* =Nt-Ct/2 (ou seja, Nt* =Nt-Ct/2), subtraímos metade dos eventos censurados).
• qt = proporção de morte (ou evento de sofrimento) durante o intervalo t, qt = Dt/Nt*
• pt = proporção de sobrevivência (evento remanescente livre) intervalo t, pt = 1-qt
• St, a proporção de sobrevivência (ou evento remanescente livre) passado intervalo t; isto é às vezes chamado de probabilidade de sobrevivência cumulativa e é calculado da seguinte forma Primeiro, a proporção de participantes sobrevivendo no tempo passado 0 (hora de início) é definida como S0 = 1 (todos os participantes vivos ou livres de evento no tempo zero ou início do estudo). A proporção de sobrevivência após cada intervalo subseqüente é computada usando princípios de probabilidade condicional introduzidos no módulo sobre Probabilidade. Especificamente, a probabilidade de um participante sobreviver ao intervalo passado 1 é S1 = p1. A probabilidade de um participante sobreviver ao intervalo passado 2 significa que ele teve que sobreviver ao intervalo passado 1 e através do intervalo 2: S2 = P(sobreviver ao intervalo passado 2) = P(sobreviver ao intervalo 2)*P(sobreviver ao intervalo passado 1), ou S2 = p2*S1. Em geral, St+1 = pt+1*St.

O formato da tabela de vida útil seguinte é mostrado abaixo.

Para o primeiro intervalo, 0-4 anos: No tempo 0, no início do primeiro intervalo (0-4 anos), há 20 participantes vivos ou em risco. Dois participantes morrem no intervalo e 1 é censurado. Aplicamos a correção para o número de participantes censurados durante esse intervalo para produzir Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. Os cálculos das restantes colunas são mostrados na tabela. A probabilidade de um participante sobreviver nos últimos 4 anos, ou passar o primeiro intervalo (usando o limite superior do intervalo para definir o tempo) é S4 = p4 = 0,897.

Para o segundo intervalo, 5-9 anos: O número em risco é o número em risco no intervalo anterior (0-4 anos) menos aqueles que morrem e são censurados (ou seja, Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17). A probabilidade de um participante sobreviver nos últimos 9 anos é S9 = p9*S4 = 0,937*0,897 = 0,840.

Intervalo em anos	Número em risco durante o intervalo, Nt	Número médio em risco durante o intervalo, Nt*	Número de mortes durante o intervalo, Dt	Perdidos para acompanhamento, Ct	Morte por Proporção Intervalo de Duração, qt	Entre os Em Risco, Sobrevivendo Proporção Intervalo, pt	Probabilidade de sobrevivência St
0-4	20	20-(1/2) = 19.5	2	1	2/19.5 = 0.103	1-0.103 = 0.897	1(0.897) = 0.897
5-9	17	17-(2/2) = 16.0	1	2	1/16 = 0.063	1-0.063 = 0.937	(0,897)(0,937)=0,840

A tabela de vida de seguimento completa é mostrada abaixo.

Intervalo em anos	Número em risco durante o intervalo, Nt	Número médio em risco durante o intervalo, Nt*	Número de mortes durante o intervalo, Dt	Perdidos para acompanhamento, Ct	Morte por Proporção Intervalo de Duração, qt	Entre aqueles em Risco, Proporção de Sobrevivência Interval, pt	Probabilidade de Sobrevivência St
0-4	20	>19.5	2	1	0.103	0.897	0.897
5-9	17	16.0	1	2	0.063	0.937	0.840
10-14	14	12.0	1	4	0.083	0.917	0.770
15-19	9	7.5	1	3	0.133	0.867	0.668
20-24	5	3.0	1	4	0.333	0,667	0,446

Esta tabela utiliza o método actuarial para construir a tábua de vida de seguimento onde o tempo é dividido em intervalos igualmente espaçados.

Kaplan-Meier (Limite do Produto) Abordagem

Uma questão com a abordagem da tábua de vida mostrada acima é que as probabilidades de sobrevivência podem mudar dependendo de como os intervalos são organizados, particularmente com amostras pequenas. A abordagem de Kaplan-Meier, também chamada de abordagem limite de produto, é uma abordagem popular que aborda esta questão ao reestimar a probabilidade de sobrevivência cada vez que um evento ocorre.

O uso apropriado da abordagem Kaplan-Meier repousa na suposição de que a censura é independente da probabilidade de desenvolver o evento de interesse e que as probabilidades de sobrevivência são comparáveis em participantes que são recrutados cedo e mais tarde para o estudo. Ao comparar vários grupos, também é importante que estas suposições sejam satisfeitas em cada grupo de comparação e que, por exemplo, a censura não é mais provável em um grupo do que em outro.

A tabela abaixo usa a abordagem Kaplan-Meier para apresentar os mesmos dados que foram apresentados acima usando a abordagem da tábua de vida. Note que iniciamos a tabela com Time=0 e Survival Probability = 1. No Tempo=0 (linha de base, ou o início do estudo), todos os participantes estão em risco e a probabilidade de sobrevivência é 1 (ou 100%). Com a abordagem de Kaplan-Meier, a probabilidade de sobrevivência é calculada usando St+1 = St*((Nt+1-Dt+1)/Nt+1). Note que os cálculos usando a abordagem de Kaplan-Meier são similares àqueles usando a abordagem da tábua de vida atuarial. A principal diferença são os intervalos de tempo, ou seja, com a abordagem da tábua de vida atuarial consideramos intervalos igualmente espaçados, enquanto que com a abordagem de Kaplan-Meier usamos tempos de eventos observados e tempos de censura. Os cálculos das probabilidades de sobrevivência estão detalhados nas primeiras linhas da tábua.

Tempo, Anos	Número em Risco Nt	Número de Mortes Dt	Número Censurado Ct	Probabilidade de sobrevivência St+1 = St*((Nt+1-Dt+1)/Nt+1)
>0	20			1
1	20	1		1*((20-1)/20) = 0.950
2	19		1	0.950*((19-0)/19)=0.950
3	18	1		0.950*((18-1)/18) = 0.897
5	17	1		0.897*((17-1)/17) = 0.844
6	16		1	0.844
9	15		1	0.844
10	14		1	0.844
11	13		1	0.844
12	12		1	0.844
13	11		1	0.844
14	10	1		0.760
17	9	1	1	0.676
18	7		1	0.676
19	6		1	0.676
21	5		1	0.676
23	4	1		0.507
	>3	>	3	>0,507

Com grandes conjuntos de dados, estes cálculos são tediosos. Entretanto, estas análises podem ser geradas por programas de computação estatística como o SAS. O Excel também pode ser usado para calcular as probabilidades de sobrevivência, uma vez que os dados são organizados por tempos e os números de eventos e tempos censurados são resumidos.

Da tabela de vida podemos produzir uma curva de sobrevivência Kaplan-Meier.

Kaplan-Meier Survival Curve for the Data Above

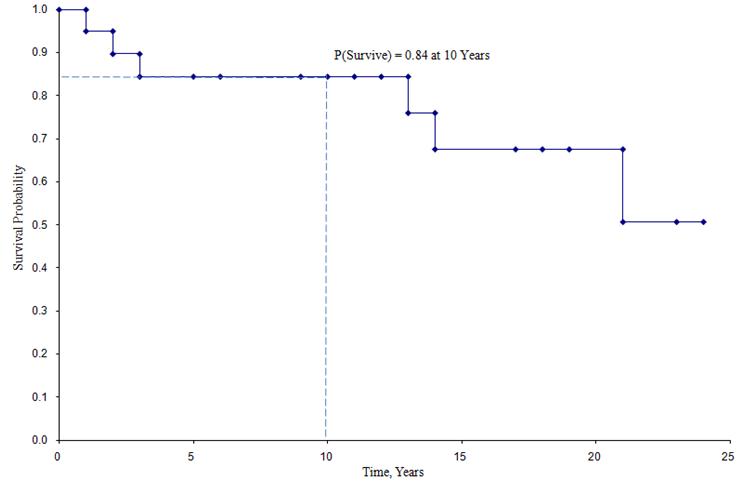
Na curva de sobrevivência mostrada acima, os símbolos representam cada tempo de evento, seja um tempo de morte ou um tempo censurado. A partir da curva de sobrevivência, podemos também estimar a probabilidade de um participante sobreviver aos 10 anos, localizando 10 anos no eixo X e lendo para cima e para cima do eixo Y. A proporção de participantes sobreviventes nos últimos 10 anos é de 84%, e a proporção de participantes sobreviventes nos últimos 20 anos é de 68%. A mediana de sobrevivência é estimada localizando 0,5 no eixo Y e lendo para cima e para baixo até o eixo X. A mediana de sobrevivência é de aproximadamente 23 anos.

Estimativas de Sobrevivência de Erros Padrão e Intervalo de Confiança

Estas estimativas de probabilidades de sobrevivência em momentos específicos e o tempo de sobrevivência mediano são estimativas pontuais e devem ser interpretadas como tal. Existem fórmulas para produzir erros padrão e estimativas de intervalos de confiança das probabilidades de sobrevivência que podem ser geradas com muitos pacotes de computação estatística. Uma fórmula popular para estimar o erro padrão das estimativas de sobrevivência é chamada fórmula Greenwoods5 e é a seguinte:

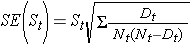
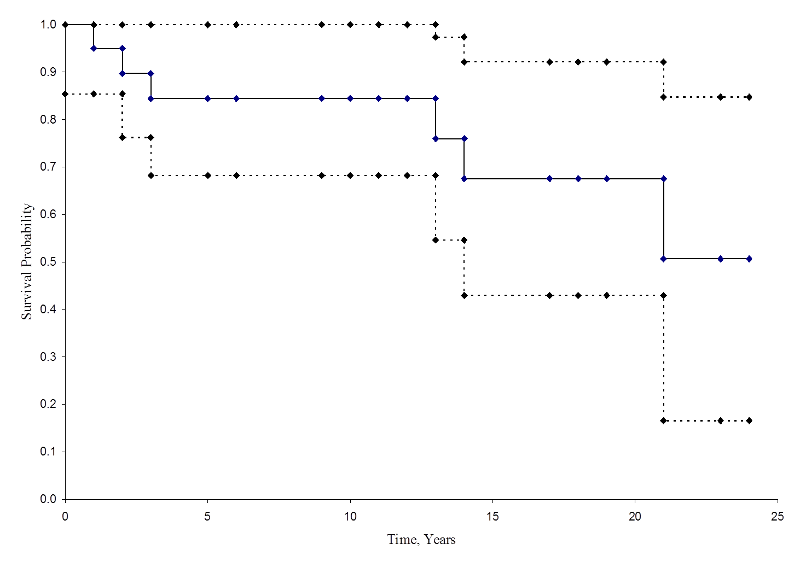
A quantidade 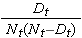é somada para números em risco (Nt) e números de mortes (Dt) que ocorrem ao longo do tempo de interesse (ou seja, cumulativo, em todos os momentos antes do tempo de interesse, ver exemplo na tabela abaixo). Os erros padrão são calculados para as estimativas de sobrevivência para os dados da tabela abaixo. Observe que a coluna final mostra a quantidade 1,96*SE(St) que é a margem de erro e usada para calcular as estimativas de intervalo de confiança de 95% (ou seja, St ± 1,96 x SE(St)).

Estimações de erro padrão de sobrevivência

Tempo, Anos	Número em risco Nt	Número de mortes Dt	Survival Probabilidade St		>		1.96*SE (St)
0	> 20		>1
1	20	1	0.950	0.003	0.003	0.049	0.096
2	19		0.950	0.000	0.003	0.049	0.096
3	18	1	0.897	0.003	0.006	0.069	0.135
5	17	1	0.844	0.004	0.010	0.083	0.162
6	16		0.844	0.000	0.010	0.083	0.162
9	15		0.844	0.000	0.010	0.083	0.162
10	14		0.844	0.000	0.010	0.083	0.162
11	13		0.844	0.000	0.010	0.083	0.162
12	12		0.844	0.000	0.010	0.083	0.162
13	11		0.844	0.000	0.010	0.083	0.162
14	10	1	0.760	0.011	0.021	0.109	0.214
17	9	1	0.676	0.014	0.035	0.126	0.246
18	7		0.676	0.000	0.035	0.126	0.246
19	6		0.676	0.000	0.035	0.126	0.246
21	5		0.676	0.000	0.035	0.126	0.246
23	4	1	0.507	0.083	0.118	0.174	0.341
24	3		0.507	0.000	0.118	0.174	0.341

A figura abaixo resume as estimativas e os intervalos de confiança na figura abaixo. A curva de sobrevivência de Kaplan-Meier é mostrada como uma linha sólida, e os limites de confiança de 95% são mostrados como linhas pontilhadas.

Kaplan-Meier Curva de Sobrevivência com Intervalos de Confiança

Curvas de Incidência Acumulativa

Alguns investigadores preferem gerar curvas de incidência cumulativa, ao contrário das curvas de sobrevivência que mostram as probabilidades cumulativas de experimentar o evento de interesse. A incidência acumulada, ou probabilidade de falha acumulada, é calculada como 1-St e pode ser calculada facilmente a partir da tabela de vida usando a abordagem Kaplan-Meier. As probabilidades cumulativas de falha para o exemplo acima são mostradas na tabela abaixo.

Tabela de Vida com Probabilidades de Falhas Acumulativas

Tempo, Anos	Número em risco Nt	Número de mortes Dt	Número Censurado Ct	Probabilidade de sobrevivência St	Probabilidade de falha 1-St
>0	20			>1	0
1	20	1		0.950	0.050
2	19		1	0.950	0.050
3	18	1		0.897	0.103
5	17	1		0.844	0.156
6	16		1	0.844	0.156
9	15		1	0.844	0.156
10	14		1	0.844	0.156
11	13		1	0.844	0.156
12	12		1	0.844	0.156
13	11		1	0.844	0.156
14	10	1		0.760	0.240
17	9	1	1	0.676	0.324
18	7		1	0.676	0.324
19	6		1	0.676	0.324
21	5		1	0.676	0.324
23	4	1		0.507	0.493
24	3		3	0.507	0,493

A figura abaixo mostra a incidência acumulada de morte dos participantes inscritos no estudo descrito acima.

Curva de Incidência Acumulativa

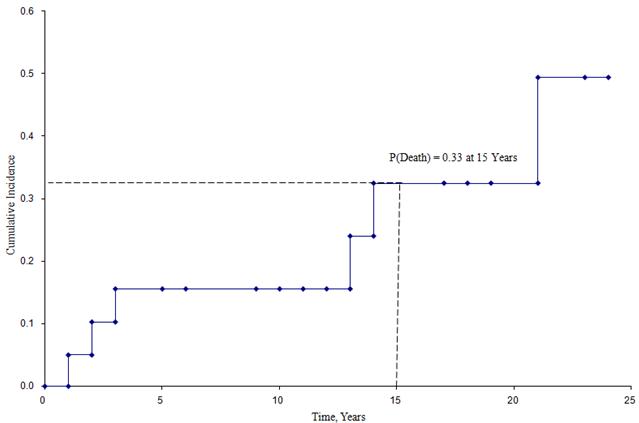
Desta figura podemos estimar a probabilidade de um participante morrer até um certo ponto de tempo. Por exemplo, a probabilidade de morte é de aproximadamente 33% aos 15 anos (ver linhas tracejadas).

volta ao topo | página anterior | página seguinte