6.3 Redes de Crenças
A noção de independência condicional pode ser usada para dar uma representação concisa de muitos domínios. A idéia é que, dada a variável arandom X, pode existir um pequeno conjunto de variáveis que afetam diretamente o valor da variável, no sentido de que X é incondicionalmente independente de outras variáveis dadas valores para as variáveis diretamente afetantes. O conjunto de variáveis que afetam localmente é chamado de Markov blanket. Esta localidade é o que é explorado na rede de crenças. Uma rede de crenças é um modelo dirigido de dependência condicional entre um conjunto de variáveis aleatórias. A declaração precisa da independência condicional na rede de crenças leva em conta a direcionalidade.
Para definir uma rede de crenças, comece com um conjunto de variáveis aleatórias que representam todas as características do modelo. Suponha que estas variáveis são {X1,…,Xn}. A seguir, selecione uma ordenação total das variáveis, X1,…,Xn.
A regra da cadeia (Proposta 6.3) mostra como decompor uma conjunção em probabilidades condicionais:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Or, em termos de variáveis aleatórias e distribuições de probabilidade,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1). >
Definir os pais da variável aleatória Xi, pais escritos(Xi), para serem um conjunto aminimal de antecessores de Xi na ordem total, de modo que os outros antecessores de Xi sejam condicionalmente independentes dos pais de Xi dados(Xi). Ou seja, pais(Xi) ⊆{X1,…,Xi-1} tal que
P(Xi|Xi-1…X1) = P(Xi|pais(Xi)).
Se existir mais de um conjunto mínimo, qualquer conjunto mínimo pode ser escolhido para ser os pais. Pode haver mais de um conjunto mínimo apenas quando alguns dos predecessores são funções determinísticas de outros.
Podemos colocar a regra da cadeia e a definição de pais juntos,dando
P(X1, X2,—, Xn) = ∏i=1n P(Xi|pais(Xi)).
A probabilidade sobre todas as variáveis, P(X1, X2,—,Xn), é chamada de distribuição conjunta de probabilidade. A rede de descrença define a afatorização da distribuição de probabilidade conjunta, onde os fatores de probabilidades condicionais são multiplicados juntos.
Uma rede de descrença, também chamada rede Bayesian, é um gráfico acíclico (DAG), onde os nós são variáveis aleatórias. Há um arco de cada elemento dos pais(Xi) em Xi. Associado à rede de crenças está um conjunto de probabilidistribuições condicionais – a probabilidade condicional de cada variável dada pelos pais (que inclui as probabilidades prévias das variáveis sem pais).
Assim, uma rede de crenças consiste em
- a DAG, onde cada nó é rotulado por uma variável aleatória;
- a domínio para cada variável aleatória; e
- um conjunto de distribuições de probabilidades condicionais dando P(X|parents(X)) para a variável P(X|parents(X)) para a variável X.
Uma rede de crenças é acíclica por construção. A forma como a cadeia governada compõe a conjunção dá a ordenação. Uma variável só pode ter predecessores como pais. Decomposições diferentes podem resultar em redes de crenças diferentes.
Ponha que usamos as seguintes variáveis, todas elas Booleanas, na seguinte ordem:
- A adulteração é verdadeira quando há adulteração do alarme.
- O fogo é verdadeiro quando há um incêndio.
- O alarme é verdadeiro quando o alarme soa.
- O fumo é verdadeiro quando há fumo.
- Sair é verdadeiro se há muitas pessoas a sair do edifício de uma só vez.
- O relatório é verdadeiro se há um relatório dado por alguém de pessoas a sair. O relatório é falso se não houver relatório de saída.
A variável Relatório denota o relatório do sensor que as pessoas estão saindo. Esta informação não é confiável porque a pessoa que emite tal relatório pode estar jogando uma brincadeira, ou ninguém que poderia ter dado tal relatório pode ter prestado atenção. Esta variável é introduzida para permitir o condicionamento de dados não confiáveis do sensor. O agente sabe o que o sensor reporta, mas só tem provas não confiáveis sobre pessoas que saem do edifício. Como parte do domínio, assuma as seguintes independências condicionais:
- Fogo é condicionalmente independente de Violação (sem dar nenhuma outra informação).
- Alarme depende tanto de Fogo como de Violação. Ou seja, não estamos fazendo suposições de independência sobre como o Alarme depende dos precedentes dados esta variável.
- A fumaça depende apenas do Fogo e é condicionalmente independente de Alteração e Alarme dado se há um Fogo.
- A saída depende apenas do Alarme e não diretamente do Fogo ou Alteração ou Fumaça. Ou seja, a Saída é condicionalmente independente das outras variáveis dadas Alarme.
- O relatório só depende diretamente da Saída.
A rede de crenças da Figura 6.1 expressa estas dependências.
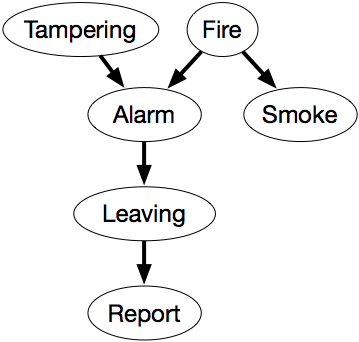
Esta rede representa a factorização
P(Tampering,Fire,Alarm,Smoke,Leaving,Relatório) = P(Fumo)×P(Fogo)×P(Alarme)×P(Alarme,Fogo) ×P(Fumo)×P(Fumo)Fogo)×P(Saída|Alarme)×P(Relatório)Saída).
Também devemos definir o domínio de cada variável. Suponha que as variáveis são booleanas; isto é, elas têm domínio {verdadeiro,falso}. Usamos a variante minúscula da variável para representar o valor verdadeiro e usamos a negação para o valor falso. Assim, por exemplo, Tampering=true é escrito como tampering, eTampering=false é escrito como ¬tampering.
Os exemplos seguintes assumem as seguintes probabilidades condicionais:
P(fire) = 0.01
P(alarm | fire ∧tampering) = 0.5
P(alarme | incêndio ∧¬tampering) = 0,99
P(alarme | incêndio ∧tampering) = 0,85
P(alarme | | incêndio ∧¬tampering) = 0,0001
P(fumo | incêndio ) = 0.9
P(smoke | ¬fire ) = 0,01
P(leaving | alarm) = 0,88
P(leaving | ¬alarm ) = 0,001
P(report | leaving ) = 0,75
P(report | ¬leaving ) = 0.01
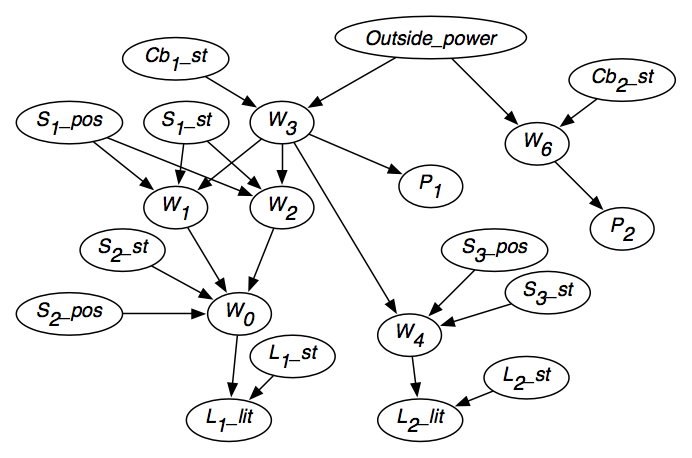
- Para cada fio wi, há uma variável aleatória, Wi, withdomain {live,dead}, que denota se há energia no fio wi. Wi=live significa que o fio wi tem potência. Wi=dead significa que não há energia no fio wi.
- Outside_power com domínio {live,dead}, que denota se há energia entrando no edifício.
- Para cada switch si, a variável Si_pos denota a posição ofsi. Ela tem o domínio {up,down}.
- Para cada switch si, a variável Si_st denota o estado do switch si. Ithas domain {ok,upside_down,short,intermittent,broken}. Si_st=ok meansswitch si está funcionando normalmente. Si_st=upside_down significa que o switchsi está instalado de cabeça para baixo. Si_st=short significa interruptor si isshorted e actua como um fio. Si_st= quebrado significa que o interruptor si está quebrado e não permite o fluxo de eletricidade.
- Para cada circuito de interrupção, a variável Cbi_st tem o domínio {on,off}. Cbi_st=on significa que a energia pode fluir através da cbi e Cbi_st=off significa que não pode fluir através da cbi.
- Para cada luz li, a variável Li_st com domínio {ok,intermitente,quebrado} denotestesta o estado da luz. Li_st=ok significa que o light li acenderá se alimentado, Li_st=intermitente significa luz li intermitente se alimentado, e Li_st= quebrado significa que o light li não funciona.
Vamos selecionar uma ordenação onde as causas de uma variável estão antes da variável na ordenação. Por exemplo, a variável para saber se uma luz está acesa depois das variáveis para saber se a luz está funcionando e se há energia entrando na luz.
Se a luz l1 está acesa depende apenas se há energia no fio w0 e se a luz l1 está a funcionar correctamente. Outras variáveis, como a posição do interruptor s1, se a luz l2 está acesa, ou quem é a rainha do Canadá, são irrelevantes. Assim, os pais de L1_lit são W0 e L1_st.
Consider variável W0, que representa se há potência no fio w0. Se soubéssemos se havia potência nos fios w1 ew2, e soubéssemos a posição do interruptor s2 e se o interruptor estava funcionando corretamente, o valor das outras variáveis (que nãoL1_lit) não afetaria nossa crença em se há potência no fio w0. Assim, os pais de W0 devem ser S2_Pos, S2_st,W1 e W2.
Figure 6.2 mostra a rede de crenças resultante após a independência de cada variável ter sido considerada.
Para a variável W1, as seguintes probabilidades condicionais devem ser especificadas:
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live)
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=vivo|S1_pos=baixo ∧S1_st=descontinuado ∧W3=morto).
Existem dois valores para S1_pos, cinco valores para S1_ok, e dois valores para W3, por isso existem 2×5 ×2 = 20 casos diferentes onde deve ser especificado um valor para W1=vivo. No que diz respeito à teoria da asprobabilidade, a probabilidade para W1=vivos para estes 20 casos poderia ser atribuída arbitrariamente. Naturalmente, o conhecimento do domínio limita quais os valores que fazem sentido. Os valores paraW1=morto podem ser calculados a partir dos valores para W1=vivo para cada um destes casos.
Porque a variável S1_st não tem pais, ela requer uma distribuição aprior, que pode ser especificada como as probabilidades para todos os valores exceto um; o valor restante pode ser derivado da restrição de que todas as probabilidades somam a 1. Assim, para especificar a distribuição de S1_st, é necessário especificar quatro das cinco probabilidades a seguir:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
Uma rede de crenças é uma representação gráfica da independência condicional. A independência permite-nos representar os efeitos directos dentro do gráfico e prescreve quais as probabilidades que devem ser especificadas. As probabilidades arbitraryposterior podem ser derivadas da rede.
A suposição de independência embutida em uma rede de crenças é a seguinte:Cada variável aleatória é condicionalmente independente de seus não-descendentes, dados os seus espíritos. Isto é, se X é uma variável aleatória com pais Y1,…, Yn, todas as variáveis aleatórias que não são descendentes deX são condicionalmente independentes de X dado Y1 ,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
se R não envolve um descendente de X. Para esta definição, incluímos X como um descendente de si mesmo. O lado da mão direita desta equação é a forma das probabilidades que são especificadas como parte da rede de crenças.R pode envolver ancestrais de X e outros nós desde que eles não sejam descendentes de X. O pressuposto de independência afirma que toda a influência de não descendentes é capturada pelo conhecimento do valor dos pais de X.
Muitas vezes, nos referimos apenas ao DAG rotulado como uma rede de crenças. Quando isto é feito, é importante lembrar que uma variável de domínio foreach e um conjunto de distribuições de probabilidade condicional também fazem parte da rede.
O número de probabilidades que devem ser especificadas para cada variável é exponencial no número de pais da variável.A suposição de independência é útil na medida em que o número de variáveis que afetam diretamente outra variável é pequeno. Você deve ordenar as variáveis de modo que os nós tenham como poucos pais possíveis.
Redes de crenças e causalidade
Redes de crenças têm sido frequentemente chamadas de redes causais e têm sido consideradas como uma boa representação da causalidade.Lembre-se que um modelo causal prevê o resultado de intervenções.Suponha que você tenha em minda modelo causal de um domínio, onde o domínio é especificado em termos de um conjunto de variáveis aleatórias. Para cada par de variáveis aleatórias X1 e X2, se existe uma conexão causal direta de X1 a X2 (ou seja, intervir para mudar X1 em algum contexto de outras variáveis afeta X2 e isto não pode ser modelado tendo alguma variável interveniente), adicione um arco de X1 a X2. Você esperaria que o modelo causal obedecesse à suposição de independência da rede de crenças. Assim, todas as conclusões da rede de crenças seriam válidas.
Você também esperaria que tal gráfico fosse acíclico; você não quer que algo eventualmente se cause a si mesmo. Esta suposição é razoável se você considerar que as variáveis aleatórias representam eventos particulares ao invés de tipos de eventos. Por exemplo, considere uma cadeia causal que “seres estressados” faz com que você “trabalhe ineficientemente”, o que, por sua vez, faz com que você “fique estressado”. Para quebrar o ciclo aparente, podemos representar “estar estressado” em diferentes estágios como diferentes variáveis aleatórias que se referem a diferentes tempos. Ser estressado no passado faz com que você não trabalhe bem no momento, o que faz com que você fique estressado no futuro. As variáveis devem satisfazer o princípio da clareza e ter um significado bem definido. As variáveis não devem ser vistas como tipos de eventos.
A própria rede de crenças não tem nada a dizer sobre a causalidade, e pode representar independência sem causa, mas parece particularmente apropriado quando há causalidade em um domínio. A adição de arcos que representam a causalidade local tende a produzir uma pequena rede de crenças. A rede de crenças deFigure 6.2 mostra como isso pode ser feito para um domínio simples.
Acausal network models interventions. Se alguém forçar artificialmente uma variável a ter um determinado valor, os descendentes da variável – mas nenhum outro nó – seriam embelezados. Finalmente, você pode ver como a causalidade nas redes de crenças se relaciona com o raciocínio causal e probatório discutido na Seção 5.7. Uma rede de crenças causais pode ser vista como afastada da axiomatização em uma direção causal. O raciocínio nas redes de crenças corresponde a raptar as causas e depois prever a partir delas. Existe um mapeamento direto entre a visão lógicaabdutora discutida na Seção 5.7 e as redes de crenças: As redes de crenças podem ser modeladas como programas lógicos comprobabilidades sobre possíveis hipóteses. Isto é descrito na Secção 14.3.
Note a restrição “cada variável aleatória é condicionalmente independente dos seus não-descendentes dados os seus espíritos” na definição da independência codificada em uma rede de crenças. SeR contém um descendente da variável X, a hipótese de independência não é directamente aplicável.
Exemplo 6.12: Na Figura 6.2, as variáveis S3_pos, S3_st, e W3 são os pais da variável W4. Se você conhece os valores de S3_pos, S3_st e W3, saber se l1 está ou não iluminada ou saber o valor de Cb1_st não afetará sua crença em se há energia no fio w4. No entanto, mesmo que soubesse os valores de S3_pos, S3_st e W3, saber se l2 é litpotencialmente muda a sua crença se há ou não poder no fio w1. A hipótese de independência não é directamente aplicável.A variável S1_pos não tem pais. Assim, a independência embutida na rede de crenças especifica que P(S1_pos=up|A) =P(S1_pos=up) para qualquer A que não envolva um descendente deS1_pos. Se A incluir um descendente de S1_pos=up – por exemplo, se A for S2_pos=up∧L1_lit=true – o pressuposto de independência não pode ser aplicado diretamente.
Esta rede pode ser usada de várias maneiras:
- Ao condicionar o conhecimento de que os switches e disjuntores estão ok, e os valores da potência externa e a posição dos switches, esta rede pode simular como a iluminação deve funcionar.
- Dados valores da potência externa e da posição dos comutadores, a rede pode inferir a probabilidade de qualquer resultado – por exemplo, quão provável é que a l1 esteja acesa.
- Valores dados para os switches e se as luzes estão acesas, a probabilidade posterior de cada switch ou disjuntor estar em qualquer estado particular pode ser inferida.
- Dadas algumas observações, a rede pode ser usada para raciocinar para trás para determinar a posição mais provável dos switches.
- Dadas algumas posições de switch, algumas saídas e alguns valores intermediários, a rede pode ser usada para determinar a probabilidade de qualquer outra variável na rede.
Uma rede de crenças especifica uma distribuição conjunta de probabilidade da qual probabilidades condicionais arbitrárias podem ser derivadas. Uma rede pode ser consultada pedindo a probabilidade condicional de quaisquer variáveis condicionadas aos valores de quaisquer outras variáveis. Isto é feito tipicamente fornecendo observações sobre algumas variáveis e conquistando outra variável.
Exemplo 6.13: Considere o Exemplo 6.10.As probabilidades anteriores (sem evidência) de cada variável podem ser computadas usando os métodos da próxima seção. As seguintes probabilidades condicionais seguem do modelo do Exemplo 6.10, até cerca de três casas decimais:P(tampering ) = 0.02
P(fire) = 0.01
P(report ) = 0.028
P(smoke) = 0.0189Observando o relatório dá o seguinte:
P(tampering|report) = 0,399
P(fire |report)= 0,2305
P(smoke |report) = 0,215Como esperado, a probabilidade de bothtampering and fire são aumentadas pelo relatório. Porque o fogo é aumentado, a probabilidade de fumaça é aumentada.
Ponha em vez disso que a fumaça foi observada:
P(tampering|smoke) = 0,02
P(fire|smoke) = 0,476
P(report |smoke) = 0,320Note que a probabilidade de tampering não é afetada pela observação de fumaça; no entanto, as probabilidades de relatório e fogo são aumentadas.
Ponha que ambos relatório e fumaça foram observados:
P(tampering |report ∧smoke) = 0,0284
P(fire |report ∧smoke) = 0,964Observar ambos torna o fogo ainda mais provável. No entanto, no contexto do relatório, a presença de fumo torna a adulteração menos provável. Isto porque o relatório é explicado pelo fogo, que agora é mais provável.
Ponha em vez disso esse relatório, mas não fumo, foi observado:
P(tampering |reportar ∧¬smoke) = 0.501
P(fire|report ∧¬smoke) = 0,0294No contexto do relatório, o fogo torna-se muito menos provável e a probabilidade de adulteração aumenta para explicar o relatório.
Este exemplo ilustra como a suposição de independência da rede de crenças dá conclusões comuns e também demonstra como a explicação da suposição de independência de uma rede de crenças é uma conseqüência.
- 6.3.1 Construindo Redes de Crenças