Na Guerra dos Mundos, robôs alienígenas gigantes emergem do chão e começam a vaporizar um grande número de actores. Há muito a gostar nessas cenas, mas há três coisas que eu não poderia suportar.
Como aquelas três pernas em que eles andavam. Não a sua fragilidade, mas as suas três pernas…

Por favor, primeiro o Tom Cruise, primeiro o Tom Cruise, por favor, …
Devia haver mais pernas. Cerca de seis delas, em particular.
“Olhe”, você pode responder, “é uma nave alienígena, e quem sabe que tipo de princípios eles descobriram”.”
De certeza, isso é possível. Mas outra maneira de ver é que nós, terráqueos, viemos em uma grande variedade de planos de corpo e membros, e ainda assim não encontramos o desenho de três membros em nenhum lugar. Talvez esse seja um bom argumento de que alienígenas não construiriam uma nave com três pernas.
O que nós terráqueos fazemos para o desenho de membros?
Tendemos a seguir uma lei, uma lei que pode atravessar todos os phyla animais, uma lei que publiquei pela primeira vez no Journal of Theoretical Biology em 2001 , e que foi elaborada no meu primeiro livro The Brain from 25,000 Feet .

Esta “lei de membros” relaciona o número de membros de um animal ao comprimento desses membros (em relação ao tamanho do corpo).
Quando os membros de um animal são muito longos em relação ao seu tamanho corporal, eu argumentei que a solução ideal de alcance (que usa a menor quantidade de “fio”, ou material de membros) é ter cerca de seis membros. (Isto se aplica a animais com membros que são aproximadamente dirigidos radialmente ao redor de um perímetro. Para animais cujas direções dos membros estão uniformemente espalhadas por uma superfície esférica, o número esperado de membros neste caso seria cerca de 12.)

Como os membros do animal encurtam em relação ao tamanho do corpo, o número esperado de membros sobe, com um tremendo número de membros quando os membros são muito curtos. (A propósito, uma cobra é consistente com muitos membros infinitamente curtos – ou seja, sem membros.)
Mais geralmente, a lei prevê que o número de membros de um animal é inversamente proporcional ao comprimento relativo dos membros. E, mais especificamente, a lei prevê uma constante de proporcionalidade particular, de modo que “seis” é a solução no caso de membros realmente longos.
Deixando L o comprimento do membro e R o raio do corpo do animal, então k = L / (L + R) é o comprimento relativo do membro, ou “relação de membros”.
O número de membros, N, deve variar aproximadamente como

N ≈ ≈/k ≈6.28 k-1
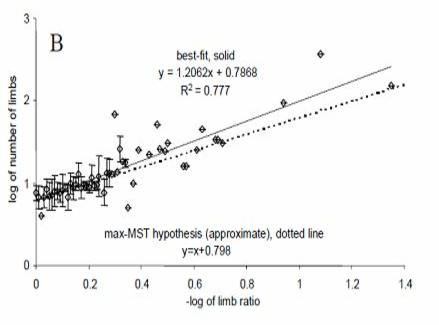
A figura abaixo (do meu primeiro livro) mostra como o número de membros de fato se relaciona com a proporção de membros, para 190 espécies através de sete phyla animais (Annelida, Arthropoda, Cnidaria, Echinodermata, Mollusca, Vertebrata, e Tardigrada).

A tendência prevista é mostrada com a linha sólida, consistente com a equação N ≈ 6.28k-1 que vimos logo acima.

A tendência real é mostrada com a linha pontilhada, levando a uma equação empírica de N ≈6.24k-1.17 … ou muito próxima da previsão.
Para ter uma melhor impressão da Lei dos Membros que os terráqueos parecem seguir, confira este pequeno programa visual dinâmico de Eric Bolz, permitindo-lhe variar o comprimento dos membros e observar como o número de membros varia: http://www.changizi.com/limb.html O eixo vertical direito permite-lhe modular a relação de membros e ver como o número de membros muda. O eixo inferior permite que você faça criaturas mais longas ou mais curtas. O eixo vertical esquerdo apenas permite redimensionar a criatura na página.
As naves alienígenas da Guerra dos Mundos devem ter – dado o comprimento dos seus membros longos e assumindo que devem ser tratadas como aproximadamente apontando em torno de um perímetro – cerca de seis membros. Não três.
É por isso que elas parecem tão bobas. Eles estão fora do ponto doce no espaço de desenho para membros.

Na minha próxima peça, vou discutir como essa idéia de membro nos diz por que temos 10 dedos, e talvez, portanto, por que temos um sistema básico de 10 números.