O Fluxo StatsTest: Predição >> Variável Dependente Contínua >> Mais de Uma Variável Independente >>Sem Medidas Repetidas >>Uma Variável Dependente

Não tem a certeza de que este é o método estatístico correcto? Use o fluxo de trabalho Choose Your StatsTest para selecionar o método correto.

O que é Regressão Linear Múltipla Variável?

Regressão Linear Múltipla Variável é um teste estatístico usado para prever múltiplas variáveis de resultados usando uma ou mais variáveis. Também é usado para determinar a relação numérica entre estes conjuntos de variáveis e outros. A variável que você deseja prever deve ser contínua e seus dados devem atender às outras suposições listadas abaixo.

Premissas para a Regressão Linear Múltipla Variável

Todos os métodos estatísticos têm suposições. Suposições significam que seus dados devem satisfazer certas propriedades para que os resultados do método estatístico sejam precisos.

As suposições para a Regressão Linear Multivariada Múltipla incluem:

1. Linearidade
2. Sem Outliers
3. Disseminação Simples através do Intervalo
4. Normalidade dos Resíduos
5. Sem Multicolinearidade

Divergir para cada um destes separadamente.

Linearidade

As variáveis que lhe interessam devem estar relacionadas de forma linear. Isto significa que se você traçar as variáveis, você será capaz de desenhar uma linha reta que se encaixa na forma dos dados.

Sem Outliers

As variáveis com as quais você se preocupa não devem conter outliers. A regressão linear é sensível a outliers, ou pontos de dados que têm valores invulgarmente grandes ou pequenos. Você pode dizer se suas variáveis têm outliers traçando-as e observando se algum ponto está longe de todos os outros pontos.

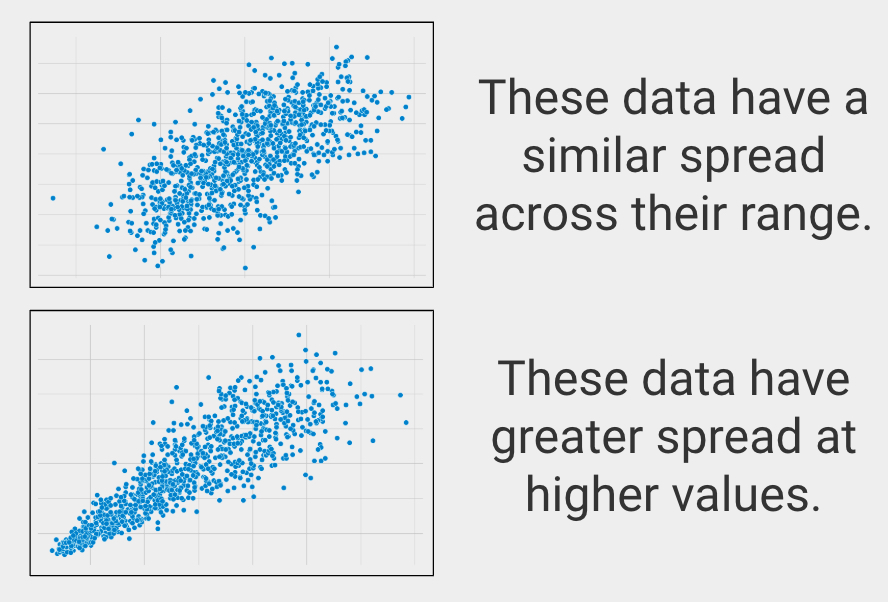
Passo similar em todo o intervalo

Na estatística isto é chamado de homoscedasticidade, que descreve quando as variáveis têm um intervalo similar em seus intervalos.

Normalidade dos resíduos

A palavra “resíduos” refere-se aos valores resultantes da subtração das variáveis dependentes esperadas (ou previstas) dos valores reais. A distribuição desses valores deve corresponder a uma forma de distribuição normal (ou curva do sino).

A realização dessa suposição assegura que os resultados da regressão são igualmente aplicáveis em toda a extensão dos dados e que não há viés sistemático na previsão.

Sem Multicolinearidade

Multicolinearidade refere-se ao cenário quando duas ou mais variáveis independentes estão substancialmente correlacionadas entre si. Quando a Multicolinearidade está presente, os coeficientes de regressão e significância estatística tornam-se instáveis e menos confiáveis, embora isso não afete a adequação do modelo aos dados per se.

Quando usar a Regressão Linear Múltipla Multivariada?

Você deve usar a Regressão Linear Múltipla e Multivariada no seguinte cenário:

1. Você quer usar uma variável em uma previsão de múltiplas outras variáveis, ou você quer quantificar a relação numérica entre elas
2. As variáveis que você quer prever (sua variável dependente) são contínuas
3. Você tem mais de uma variável independente, ou uma variável que você está usando como preditor
4. Você não tem medidas repetidas da mesma unidade de observação
5. Você tem mais de uma variável dependente

Vamos esclarecer estas para ajudá-lo a saber quando usar a Regressão Linear Múltipla.

Previsão

Você está procurando por um teste estatístico para prever uma variável usando outra. Esta é uma questão de predição. Outros tipos de análises incluem examinar a força da relação entre duas variáveis (correlação) ou examinar diferenças entre grupos (diferença).

Variável Dependente Contínua

A variável que você deseja predizer deve ser contínua. Contínua significa que sua variável de interesse pode basicamente assumir qualquer valor, como freqüência cardíaca, altura, peso, número de barras de sorvete que você pode comer em 1 minuto, etc.

Tipos de dados que NÃO são contínuos incluem dados encomendados (como o lugar de chegada em uma corrida, melhores classificações de negócios, etc.), dados categóricos (sexo, cor dos olhos, raça, etc.), ou dados binários (comprado o produto ou não, tem a doença ou não, etc.).

Se sua variável dependente for binária, você deve usar Regressão Logística Múltipla, e se sua variável dependente for categórica, então você deve usar Regressão Logística Multinomial ou Análise Discriminatória Linear.

Mais que uma variável independente

Regressão linear múltipla é usada quando há uma ou mais variáveis preditoras com múltiplos valores para cada unidade de observação.

Sem medidas repetidas

Este método é adequado para o cenário quando há apenas uma observação para cada unidade de observação. A unidade de observação é o que compõe um “ponto de dados”, por exemplo, uma loja, um cliente, uma cidade, etc…

Se você tiver uma ou mais variáveis independentes mas elas são medidas para o mesmo grupo em vários pontos no tempo, então você deve usar um Modelo de Efeitos Mistos.

Mais de uma variável dependente

Para executar a Regressão Linear Múltipla Variável, você deve ter mais de uma variável dependente, ou variável que você está tentando prever.

Se você estiver prevendo apenas uma variável, você deve usar a Regressão Linear Múltipla.

Exemplo de Regressão Linear Múltipla Variável

Variável Dependente 1: Receita
Variável dependente 2: Tráfego de clientes
Variável independente 1: Dólares gastos em publicidade por cidade
Variável Independente 2: População da cidade

A hipótese nula, que é linguagem estatística para o que aconteceria se o tratamento não fizesse nada, é que não há relação entre os gastos em publicidade e os dólares ou população publicitária por cidade. Nosso teste irá avaliar a probabilidade desta hipótese ser verdadeira.

Reagrupamos nossos dados e após assegurar que as suposições de regressão linear são cumpridas, realizamos a análise.

Esta análise efetivamente executa a regressão linear múltipla duas vezes usando ambas as variáveis dependentes. Assim, quando executamos esta análise, obtemos coeficientes beta e p-valores para cada termo no modelo “receita” e no modelo “tráfego de clientes”. Para qualquer modelo de regressão linear, você terá um coeficiente beta igual à intercepção da sua linha de regressão linear (muitas vezes etiquetada com um 0 como β0). Isto é simplesmente onde a linha de regressão atravessa o eixo y se você fosse traçar seus dados. No caso da regressão linear múltipla, existem ainda mais dois outros coeficientes beta (β1, β2, etc), que representam a relação entre as variáveis independentes e dependentes.

Estes coeficientes beta adicionais são a chave para compreender a relação numérica entre as suas variáveis. Essencialmente, para cada unidade (valor de 1) de aumento em uma determinada variável independente, espera-se que sua variável dependente mude pelo valor do coeficiente beta associado a essa variável independente (mantendo constantes outras variáveis independentes).

O valor p associado a esses valores beta adicionais é a chance de ver nossos resultados assumindo que realmente não há relação entre essa variável e a receita. Um p-valor menor ou igual a 0,05 significa que nosso resultado é estatisticamente significativo e podemos confiar que a diferença não é devida apenas ao acaso. Para obter um valor de p global para o modelo e valores de p individuais que representam os efeitos das variáveis nos dois modelos, são frequentemente utilizados MANOVAs.

Além disso, esta análise resultará num valor R-Squared (R2). Este valor pode variar de 0-1 e representa o quão bem a sua linha de regressão linear se ajusta aos seus pontos de dados. Quanto maior o R2, melhor o seu modelo se ajusta aos seus dados.

Frequently Asked Questions

Q: Qual é a diferença entre regressão linear múltipla multivariada e regressão linear em execução múltiplas vezes?
A: São conceptualmente semelhantes, pois os coeficientes individuais do modelo serão os mesmos em ambos os cenários. Uma diferença substancial, entretanto, é que testes de significância e intervalos de confiança para a regressão linear multivariada contabilizam as variáveis múltiplas dependentes.

Q: Como eu executo a Regressão Linear Múltipla Multivariada em SPSS, R, SAS, ou STATA?
A: Este recurso está focado em ajudá-lo a escolher sempre o método estatístico correto. Há muitos recursos disponíveis para ajudá-lo a descobrir como executar este método com os seus dados:
R artigo: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/

Ajuda!

Se você ainda não consegue descobrir algo, sinta-se à vontade para chegar lá.