De Evan Ma

(meditator la matematică și fizică la The Edge Learning Center)

Funcția logaritmică pare să îi încurce pe mulți elevi care studiază programul IB Math SL. Pentru a o înțelege corect, să definim

unde , un număr real strict pozitiv, se numește baza, iar este puterea. De exemplu, cu toții știm pe de rost următoarele:

și așa mai departe. Funcția logaritmică procedează invers – având ca argument un număr, ea produce puterea supusă unei baze specificate și, prin urmare, este definită după cum urmează.

Dacă

atunci

Prin urmare, este clar că

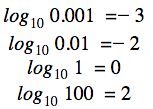
și așa mai departe. Să analizăm și alte exemple care implică alte baze:

Să completăm următoarele întrebări ca exercițiu: (a) , (b) , (c) , (d) . Răspunsurile se găsesc la sfârșitul acestui blog.

Din definiția logaritmului, putem vedea și că dacă ridicăm baza cu baza-logaritmului unui număr real , vom obține înapoi numărul , și anume

Puteți încerca să verificați acest lucru folosind calculatorul dumneavoastră pentru diferite baze valide. Această identitate este importantă atunci când încercăm să rezolvăm ecuații logaritmice, ale căror exemple vor fi date după.

Acum, să aruncăm o privire la regulile logaritmului. La fel ca în cazul definiției logaritmului, folosim legile indicilor pentru a deriva regulile:

1. Logaritmul unui produs este suma logaritmilor

Probă: Să zicem și , deci

2. Logaritmul de bază al lui Mr este ori

Probă: Spunem , deci

3. Logaritmul unui coeficient este diferența logaritmilor

Probă: Spunem și , deci

4. Ultima regulă se numește formula de schimbare a bazei. Vom folosi un exemplu ca instrument pentru a deduce formula. Să presupunem că vrem să știm ce putere trebuie să fie ridicată la 2 pentru a obține 50. Deoarece 50 nu este o putere întreagă a lui 2, răspunsul nu este foarte evident. Prin urmare, scriem

și deci. Pentru a găsi , să spunem că aplicăm logaritmul în baza 10 la ambele părți ale ecuației, deoarece calculatorul nostru s-ar putea să nu aibă tasta logaritm în baza 2:

Corectată la 4 cifre semnificative, valoarea lui este de aproximativ 5,644. De fapt, puteți verifica răspunsul dvs. ridicând 2 la puterea lui 5,644 pentru a vedea că răspunsul este de aproximativ 50.

Pentru a generaliza problema, să spunem că trebuie să găsim astfel încât și logaritmul de bază să nu fie la dispoziția noastră, prin urmare, putem folosi în schimb logaritmul de bază- conform ecuației

și deci

Cu titlu de exemplu, să considerăm următoarele. Să presupunem că o sumă de 10.000 de dolari este depusă la o dobândă de 2,5% pe an, compusă anual. Cât timp trebuie să fie păstrați banii în cont pentru ca aceștia să crească până la 50.000 de dolari?

Pentru a răspunde la întrebare, practic încercăm să găsim n astfel încât

Pentru că simplul meu calculator științific nu-mi permite să specific o bază de 1.025 pentru cheia logaritmică, va trebui să mă bazez pe formula de schimbare a bazei și să folosesc baza 10 și, prin urmare

Dacă dobânda se compune anual, va fi nevoie de 66 de ani pentru a crește de cel puțin 5 ori.

După ce am explorat regulile logaritmilor, introducem funcția logaritmică naturală, sau . Ea este baza-, unde este eminentul număr irațional ≈2,71828 și a cărui importanță în științe și matematică nu poate fi subliniată îndeajuns. Așadar, baza-logaritmul se definește astfel:

Dacă

atunci

În continuare, să vedem două exemple în care se fac greșeli frecvente în rezolvarea ecuațiilor de logaritmi. Vedeți dacă puteți identifica greșeala.

Unde este greșeala? Priviți mai atent. Bineînțeles, în al doilea pas, nu se poate “împărți” logaritmul peste semnul de adunare. Nu uitați că se poate “împărți” un logaritm într-o sumă doar dacă logaritmul este aplicat unui produs, nu unei sume. Pașii corecți sunt, prin urmare, următorii:

Acum, să ne uităm la următorul exemplu și să vedem dacă puteți identifica greșeala:

Unde este greșeala? Da, este în al doilea pas – un coeficient de logaritmi nu este, bineînțeles, logaritmul coeficientului. Mai degrabă, putem folosi formula de schimbare a bazei pentru a simplifica primul pas, după cum urmează:

În cele din urmă, vom ilustra cum să folosim regulile logaritmilor pentru a rezolva următoarea problemă:

Puteți observa că necunoscuta apare ca bază și ca variabilă în argumentul logaritmului. Cum putem rezolva pentru ? Metoda depinde în continuare de aplicarea consecventă a regulilor logaritmului. În primul rând, ridicăm ambele părți ca puteri ale bazei și, prin urmare

Vă amintiți din definiția logaritmului că partea stângă va deveni doar argumentul logaritmului, și, prin urmare,

Rezolvând ecuația de mai sus, trebuie să rezolvăm

Observând că aceasta seamănă cu o cuadratură în , rezolvăm pentru după cum urmează:

Acum, unde este rădăcina negativă? Deoarece este, de asemenea, baza logaritmului, rădăcina negativă este, prin urmare, respinsă ca soluție. Prin urmare, este răspunsul final.

Revizuind exemplele de mai sus, puteți vedea că rezolvarea unei ecuații logaritmice aparent dificile nu este deloc dificilă – este suficient să aplicați regulile logaritmului în mod consecvent și se poate obține soluția corectă.

Răspunsuri la întrebări: (a) 2 (b) 3 (c) -3 (d) -2.

.