Grafuri în Python

Origini ale teoriei grafurilor

Înainte de a începe cu implementările propriu-zise ale grafurilor în Python și înainte de a începe cu introducerea modulelor Python care se ocupă de grafuri, dorim să ne dedicăm originilor teoriei grafurilor.
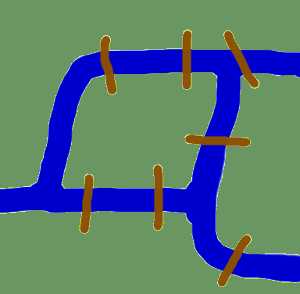
Originile ne duc înapoi în timp, la Künigsberg în secolul al XVIII-lea. La acea vreme, Königsberg era un oraș din Prusia. Râul Pregel curgea prin oraș, creând două insule. Orașul și insulele erau conectate prin șapte poduri, așa cum se arată în imagine. Locuitorii orașului au fost mișcați de întrebarea dacă ar fi posibil să se facă o plimbare prin oraș, vizitând fiecare zonă a orașului și traversând fiecare pod doar o singură dată? Fiecare pod trebuie să fi fost traversat în întregime, adică nu este permisă parcurgerea pe jumătate a unui pod și apoi întoarcerea și traversarea ulterioară a celeilalte jumătăți din cealaltă parte. Nu este necesar ca plimbarea să înceapă și să se termine în același loc.Leonhard Euler a rezolvat problema în 1735 demonstrând că acest lucru nu este posibil. El a descoperit că alegerea unui traseu în interiorul fiecărei zone de teren este irelevantă și că singurul lucru care contează este ordinea (sau secvența) în care sunt traversate podurile. El a formulat o abstractizare a problemei, eliminând faptele inutile și concentrându-se asupra zonelor de uscat și a podurilor care le conectează. În acest fel, el a creat bazele teoriei grafurilor. Dacă privim o “zonă de teren” ca pe un vârf și fiecare pod ca pe o muchie, am “redus” problema la un graf.

Introducere în teoria grafurilor folosind Python

Înainte de a începe tratatul nostru despre posibilele reprezentări Python ale grafurilor, dorim să prezentăm câteva definiții generale ale grafurilor și ale componentelor sale.
Un “graf “1 în matematică și informatică este format din “noduri”, cunoscute și sub numele de “vârfuri”.Nodurile pot fi sau nu conectate între ele. În ilustrația noastră, – care este o reprezentare picturală a unui graf, – nodul “a” este conectat cu nodul “c”, dar “a” nu este conectat cu “b”. Linia de legătură dintre două noduri se numește muchie. În cazul în care marginile dintre noduri nu sunt direcționate, graful se numește graf nedirijat. Dacă o muchie este dirijată de la un vârf (nod) la altul, un graf se numește graf dirijat. O muchie dirijată se numește arc.
Deși grafurile pot părea foarte teoretice, multe probleme practice pot fi reprezentate prin grafuri. Acestea sunt adesea folosite pentru a modela probleme sau situații în fizică, biologie, psihologie și, mai ales, în informatică. În informatică, grafurile sunt folosite pentru a reprezenta rețelele de comunicații, organizarea datelor, dispozitivele de calcul, fluxul de calcul,

În acest din urmă caz, grafurile sunt folosite pentru a reprezenta organizarea datelor, cum ar fi sistemul de fișiere al unui sistem de operare, sau rețelele de comunicații. Structura de legături a site-urilor web poate fi văzută, de asemenea, ca un graf, adică un graf direcționat, deoarece o legătură este o muchie sau un arc direcționat.
Python nu are un tip de date sau o clasă încorporată pentru grafuri, dar este ușor de implementat în Python. Un tip de date este ideal pentru reprezentarea grafurilor în Python, și anume dicționarele. Graficul din ilustrația noastră poate fi implementat în felul următor:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Celele dicționarului de mai sus sunt nodurile grafului nostru. Valorile corespunzătoare sunt liste cu nodurile, care sunt conectate prin intermediul unei muchii. Nu există un mod mai simplu și mai elegant de a reprezenta un graf.
O muchie poate fi văzută ca o 2-tuplă cu nodurile ca elemente, adică (“a”, “b”)
Funcție pentru a genera lista tuturor muchiilor:Acest cod generează următoarea ieșire, dacă este combinat cu dicționarul de graf definit anterior:

 $ python3 graph_simple.py 

După cum putem vedea, nu există nicio muchie care să conțină nodul “f”. “f” este un nod izolat al grafului nostru.
Următoarea funcție Python calculează nodurile izolate ale unui graf dat:Dacă apelăm această funcție cu graful nostru, va fi returnată o listă care conține “f”:

Graphs as a Python Class

Înainte de a continua cu scrierea de funcții pentru grafuri, avem o primă încercare de implementare a unei clase de grafuri Python. Dacă vă uitați la următoarea listă a clasei noastre, puteți vedea în metoda __init__ că folosim un dicționar “self.__graph_dict” pentru stocarea vârfurilor și a vârfurilor adiacente corespunzătoare.
Dacă porniți acest modul de sine stătător, veți obține următorul rezultat:

Cale în grafuri

Vrem să găsim acum cea mai scurtă cale de la un nod la un alt nod. Înainte de a ajunge la codul Python pentru această problemă, va trebui să prezentăm câteva definiții formale.
Vârfuri adiacente:
Două vârfuri sunt adiacente atunci când ambele sunt incidente pe o muchie comună.
Calea într-un graf nedirijat:
O cale într-un graf nedirijat este o secvență de vârfuri P = ( v1, v2, …., vn ) ∈ V x V x V x … x V astfel încât vi este adiacentă lui v{i+1} pentru 1 ≤ i < n. O astfel de cale P se numește cale de lungime n de la v1 la vn.
Calea simplă:
O cale fără vârfuri repetate se numește cale simplă.
Exemplu:
(a, c, e) este o cale simplă în graful nostru, la fel ca și (a,c,e,b). (a,c,e,b,c,d) este o traiectorie, dar nu este o traiectorie simplă, deoarece nodul c apare de două ori.

Metoda următoare găsește o traiectorie de la un vârf inițial la un vârf final:Dacă salvăm clasa noastră de grafuri care include metoda find_path sub numele de “graphs.py”, putem verifica modul de lucru al funcției noastre find_path:Rezultatul programului anterior arată astfel:
Metoda find_all_paths găsește toate căile dintre un vertex de început și un vertex de sfârșit:Am modificat ușor graficul nostru de exemplu prin adăugarea de muchii de la “a” la “f” și de la “f” la “d” pentru a testa metoda definită anterior:Rezultatul arată astfel:

Degree

Degreele unui vertex v dintr-un graf este numărul de muchii care îl conectează, buclele fiind numărate de două ori. Gradul unui vertex v se notează deg(v). Gradul maxim al unui graf G, notat cu Δ(G), și gradul minim al unui graf, notat cu δ(G), sunt gradul maxim și minim al vârfurilor sale.
În graful din partea dreaptă, gradul maxim este 5 la vîrful c, iar gradul minim este 0, adică vîrful izolat f.
Dacă toate gradele dintr-un graf sunt aceleași, graful este un graf regulat. într-un graf regulat, toate gradele sunt aceleași, și astfel putem vorbi de gradul grafului.
Formula sumei gradelor (lema Handshaking):
∑v &in; Vdeg(v) = 2 |E|
Aceasta înseamnă că suma gradelor tuturor vârfurilor este egală cu numărul de muchii înmulțit cu 2.Putem concluziona că numărul de vârfuri cu grad impar trebuie să fie par. Această afirmație este cunoscută sub numele de lema handshaking. Numele de “handshaking lemma” provine de la o problemă matematică populară: În orice grup de oameni, numărul de persoane care au dat mâna cu un număr impar de alte persoane din grup este par.
Această metodă calculează gradul unui vârf:
Această metodă calculează o listă care conține vârfurile izolate ale unui graf:Metodele delta și Delta pot fi folosite pentru a calcula gradul minim și respectiv maxim al unui vârf:

Succesiunea de grade

Succesiunea de grade a unui graf neorientat este definită ca fiind secvența de grade ale vertexurilor sale într-o ordine non-crescătoare.
Metoda următoare returnează o tupla cu secvența de grade a grafului de instanță:
Secvența de grade a grafului nostru de exemplu este următoarea secvență de numere întregi: (5,2,1,1,1,0).
Grafurile izomorfe au aceeași secvență de grade. Cu toate acestea, două grafuri cu aceeași secvență de grade nu sunt neapărat izomorfe.
Există întrebarea dacă o anumită secvență de grade poate fi realizată de un graf asimplu. Teorema Erdös-Gallai afirmă că o secvență non-crescătoare de n numere di (pentrui = 1, …., n) este secvența de grade a unui graf simplu dacă și numai dacă suma secvenței este pară și dacă este îndeplinită următoarea condiție:

Implementarea teoremei Erdös-Gallai

Clasa noastră de grafuri – a se vedea mai jos pentru o listă completă – conține o metodă “erdoes_gallai” care decide, dacă o secvență îndeplinește teorema Erdös-Gallai. În primul rând, verificăm dacă suma elementelor secvenței este impară. În caz afirmativ, funcția returnează False, deoarece teorema Erdös-Gallai nu mai poate fi îndeplinită. După aceasta, verificăm cu ajutorul metodei statice is_degree_sequence dacă secvența de intrare este o secvență de grade, adică dacă elementele secvenței nu sunt crescătoare. Acest lucru este oarecum superfluu, deoarece se presupune că intrarea trebuie să fie o secvență de grade, așa că puteți renunța la această verificare pentru eficiență. Acum, verificăm în corpul celei de-a doua declarații if, dacă este îndeplinită inecuația teoremei:
Versiune fără testul secvenței de grade superflue:

Densitatea grafului

Densitatea grafului este definită ca fiind raportul dintre numărul de muchii ale unui anumit graf și numărul total de muchii pe care le-ar putea avea graful. Cu alte cuvinte: Ea măsoară cât de aproape este un anumit graf de un graf complet.
Densitatea maximă este 1, dacă un graf este complet. Acest lucru este clar, deoarece numărul maxim de muchii dintr-un graf depinde de vârfuri și poate fi calculat astfel:
numărul maxim de muchii = ½ * |V| * ( |V| – 1 ).
Pe de altă parte, densitatea minimă este 0, dacă graful nu are muchii, adică este un graf izolat.
Pentru grafurile simple neorientate, densitatea grafului se definește astfel: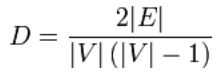

Un graf dens este un graf în care numărul de muchii este apropiat de numărul maxim de muchii. Un graf cu doar câteva muchii, se numește graf rarefiat. Definiția pentru acești doi termeni nu este foarte precisă, adică nu există cea mai mică limită superioară (supremum) pentru o densitate rară și nici cea mai mare limită inferioară (infimum) pentru definirea unui graf dens.
Cea mai precisă notație matematică folosește notația O mare:
Graf rar:
Grafic dens:
Un graf dens este un graf G = (V, E) în care |E| = Θ(|V|2).
“densitate” este o metodă a clasei noastre pentru a calcula densitatea unui graf:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Putem testa această metodă cu următorul script. Un graf complet are o densitate de 1, iar un graf izolat are o densitate de 0, după cum putem vedea din rezultatele scriptului de testare anterior:

$ python test_density.py 0.4666666666671.00.0

Grafuri conectate

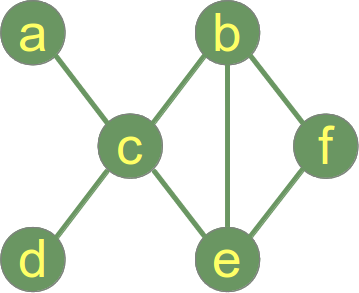Se spune că un graf este conectat dacă fiecare pereche de vârfuri din graf este conectată. Graficul de exemplu din dreapta este un graf conex.
Se poate determina cu un algoritm simplu dacă un graf este conex:

1. Alegeți un nod arbitrar x din graful G ca punct de plecare
2. Determinați setul A al tuturor nodurilor la care se poate ajunge din x.
3. Dacă A este egal cu setul de noduri din G, graful este conectat; în caz contrar, este deconectat.

Implementăm o metodă is_connected pentru a verifica dacă un graf este un graf conectat. Nu punem accentul pe eficiență, ci pe lizibilitate.
Dacă adăugăm această metodă la clasa noastră graf, o putem testa cu următorul script. Presupunând că ați salvat clasa de graf sub numele graph2.py:
O componentă conectată este un subgraf conectat maxim al lui G. Fiecare vârf aparține exact unei componente conectate, la fel ca fiecare muchie.

Distanța și diametrul unui graf

Distanța “dist” dintre două vârfuri dintr-un graf este lungimea celei mai scurte căi dintre aceste vârfuri. Pentru calculul unei distanțe nu sunt permise întoarceri, ocolișuri sau bucle.
În graficul nostru de exemplu din dreapta, distanța dintre vârful a și vârful f este 3, adică dist(a,f) = 3, deoarece drumul cel mai scurt este prin vârfurile c și e (sau alternativ c și b).
Excentricitatea unui vârf s al unui graf g este distanța maximă față de orice alt vârf al grafului:
e(s) = max( { dist(s,v) | v ∈ V })
(V este ansamblul tuturor vârfurilor din g)
Diametrul d al unui graf este definit ca fiind excentricitatea maximă a oricărui vârf din graf. Aceasta înseamnă că diametrul este lungimea celei mai scurte căi între cele mai îndepărtate noduri. Pentru a determina diametrul unui graf, găsiți mai întâi cea mai scurtă cale între fiecare pereche de vârfuri. Cea mai mare lungime a oricăreia dintre aceste căi este diametrul grafului.
Potem vedea direct în graficul nostru de exemplu că diametrul este 3, deoarece lungimea minimă între a și f este 3 și nu există nicio altă pereche de vârfuri cu o cale mai lungă.
Metoda următoare implementează un algoritm de calcul al diametrului. Putem calcula diametrul grafului nostru de exemplu cu următorul script, presupunând din nou, că clasa noastră completă de graf este salvată sub numele de graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Se va imprima valoarea 3.

Clasa Python Graph completă

În următorul cod Python, găsiți modulul complet al clasei Python cu toate metodele discutate:graph2.py

Arbore / Pădure

Un arbore este un graf neorientat care nu conține cicluri. Acest lucru înseamnă că orice două vârfuri ale grafului sunt conectate prin exact o cale simplă.
O pădure este o uniune disjunctă de arbori. Spre deosebire de pădurile din natură, o pădure în teoria grafurilor poate fi formată dintr-un singur arbore!
Un graf cu un singur vârf și nici o muchie este un arbore (și o pădure).
Un exemplu de arbore: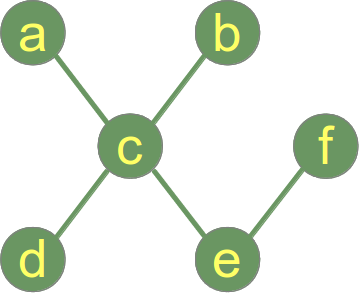

În timp ce exemplul anterior descrie un graf care este un arbore și o pădure, următoarea imagine prezintă un graf care este format din doi arbori, i.adică graful este o pădure, dar nu un arbore:

Vizualizare generală a pădurilor:

Cu un singur vârf:

Grafuri forestiere cu două vârfuri:

Grafuri forestiere cu trei vârfuri:

Arbore de cuprindere

Un arbore de cuprindere T al unui graf conex și nedirecționat G este un subgraf G’ al lui G, care este un arbore,iar G’ conține toate vârfurile și un subset de muchii ale lui G. G’ conține toate muchiile lui G, dacă G este un graf arbore. Din punct de vedere informal, un arbore de cuprindere al lui G este o selecție de muchii ale lui G care formează un arbore care cuprinde fiecare vârf. Adică, fiecare vârf se află în arbore, dar nu sunt conținute cicluri (sau bucle).
Exemplu:
Un graf complet conectat: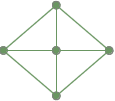

Doi arbori de cuprindere din graful complet conectat anterior: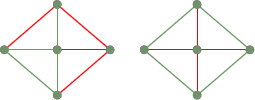

Jocul Hamiltonian

O traiectorie Hamiltoniană este o traiectorie într-un graf nedirijat sau direcționat care vizitează fiecare vertex exact o dată. Un ciclu (sau un circuit) hamiltonian este o cale hamiltoniană care este un ciclu.
Nota pentru informaticieni: În general, nu este posibil să se determine dacă astfel de căi sau cicluri există în grafuri arbitrare, deoarece problema căilor hamiltoniene s-a dovedit a fi NP-completă.
Acesta este numit după William Rowan Hamilton, care a inventat așa-numitul “joc icosian”, sau puzzle-ul lui Hamilton, care presupune găsirea unui ciclu hamiltonian în graful de muchii al dodecaedrului. Hamilton a rezolvat această problemă folosind calculul icosian, o structură algebrică bazată pe rădăcini de unitate cu multe asemănări cu quaternionii, pe care tot el i-a inventat.

Listarea completă a clasei Graph

Putem testa această clasă Graph cu următorul program:Dacă pornim acest program, vom obține următoarea ieșire:
Notele de subsol:
1 Grafurile studiate în teoria grafurilor (și în acest capitol al tutorialului nostru Python) nu trebuie confundate cu grafurile funcțiilor
2 Un singleton este un set care conține exact un singur element.
Credințe:
Narayana Chikkam, nchikkam(at)gmail(dot)com, a semnalat o eroare de indexare în metoda “erdoes_gallai”. Îți mulțumesc foarte mult, Narayana!
.