În capitolul anterior, am discutat despre Latches. Acestea sunt blocurile de bază ale flip-flops-urilor. Putem implementa flip-flops în două metode.
În prima metodă, se pun în cascadă două zăbrele în așa fel încât prima zăbrele să fie activată la fiecare impuls de ceas pozitiv și a doua zăbrele să fie activată la fiecare impuls de ceas negativ. Astfel încât combinația acestor două zăbrele să devină un flip-flop.
În a doua metodă, putem implementa direct flip-flop-ul, care este sensibil la front. În acest capitol, să discutăm următoarele flip-flops folosind a doua metodă.
- SR Flip-Flop
- D Flip-Flop
- JK Flip-Flop
- T Flip-Flop
SR Flip-Flop
SR flip-flop funcționează numai cu tranziții de ceas pozitive sau tranziții de ceas negative. În timp ce, SR latch funcționează cu semnal de activare. Schema de circuit a flip-flop-ului SR este prezentată în figura următoare.
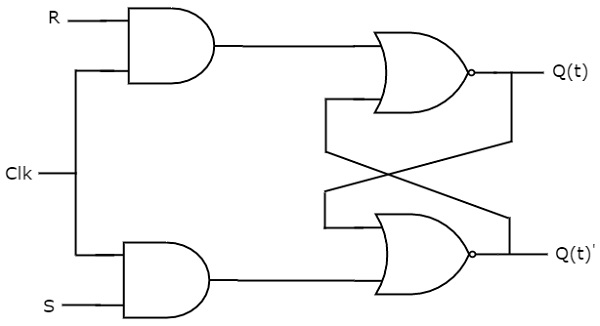
Acest circuit are două intrări S & R și două ieșiri Q(t) & Q(t)’. Funcționarea flip-flop-ului SR este similară cu cea a SR Latch-ului. Dar, acest flip-flop afectează ieșirile numai atunci când se aplică tranziția pozitivă a semnalului de ceas în loc de activarea activă.
Tabelul următor prezintă tabelul de stări al flip-flop-ului SR.
| S | R | Q(t + 1) |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | – |
Aici, Q(t) & Q(t + 1) sunt starea prezentă & respectiv următoarea stare. Așadar, flip-flop-ul SR poate fi utilizat pentru una dintre aceste trei funcții, cum ar fi Hold, Reset & Set în funcție de condițiile de intrare, atunci când se aplică tranziția pozitivă a semnalului de ceas. Tabelul următor prezintă tabelul caracteristic al flip-flop-ului SR.
| Intrări prezente | Stare prezentă | ||||
|---|---|---|---|---|---|
| S | R | Q(t) | Q(t + 1) | ||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 1 | 1 | 0 | ||
| 1 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | x | ||
| 1 | 1 | 1 | 1 | 1 | x |
Cu ajutorul celor trei variabile K-Harta, putem obține expresia simplificată pentru următoarea stare, Q(t + 1). Harta K cu trei variabile pentru următoarea stare, Q(t + 1) este prezentată în figura următoare.
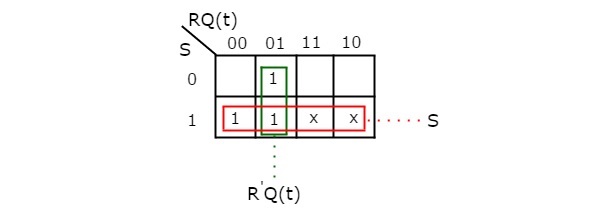
Grupările maxime posibile ale celor adiacente sunt deja prezentate în figură. Prin urmare, expresia simplificată pentru starea următoare Q(t + 1) este
$Q\left ( t+1 \right )=S+{R}’Q\left ( t \right )$
D Flip-Flop
D flip-flop funcționează numai cu tranziții de ceas pozitive sau tranziții de ceas negative. În timp ce D latch funcționează cu semnalul de activare. Aceasta înseamnă că ieșirea flip-flopului D este insensibilă la modificările de la intrarea D, cu excepția tranziției active a semnalului de ceas. Schema de circuit a flip-flop-ului D este prezentată în figura următoare.
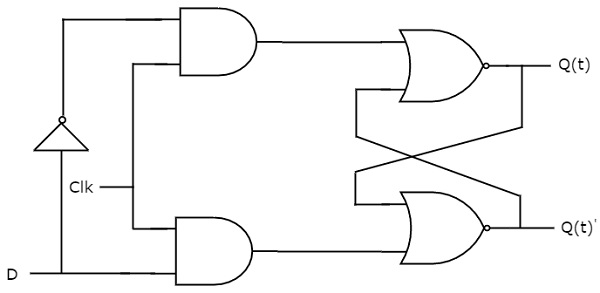
Acest circuit are o singură intrare D și două ieșiri Q(t) & Q(t)’. Funcționarea flip-flop-ului D este similară cu cea a D Latch-ului. Dar, acest flip-flop afectează ieșirile numai atunci când se aplică tranziția pozitivă a semnalului de ceas în loc de activarea activă.
Tabelul următor prezintă tabelul de stări al flip-flop-ului D.
| D | Qt + 1t + 1 | |
|---|---|---|
| 0 | 0 | |
| 1 | 1 | 1 |
În consecință, D flip-flop păstrează întotdeauna informația, care este disponibilă pe intrarea de date, D din tranziția pozitivă anterioară a semnalului de ceas. Din tabelul de stări de mai sus, putem scrie direct ecuația stării următoare ca
Q(t + 1) = D
Starea următoare a flip-flop-ului D este întotdeauna egală cu intrarea de date, D pentru fiecare tranziție pozitivă a semnalului de ceas. Prin urmare, flip-flopurile D pot fi utilizate în registre, registre de decalare și în unele dintre contoare.
JK Flip-Flop
JK flip-flop este versiunea modificată a flip-flopului SR. Acesta funcționează numai cu tranziții de ceas pozitive sau tranziții de ceas negative. Schema de circuit a flip-flopului JK este prezentată în figura următoare.
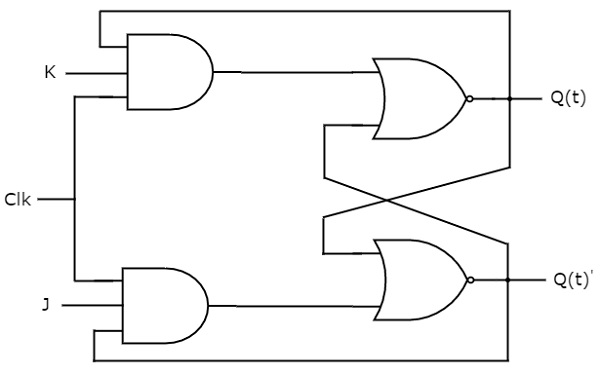
Acest circuit are două intrări J & K și două ieșiri Q(t) & Q(t)’. Funcționarea flip-flopului JK este similară cu cea a flip-flopului SR. Aici, am considerat intrările flip-flop-ului SR ca fiind S = J Q(t)’ și R = KQ(t) pentru a utiliza flip-flop-ul SR modificat pentru 4 combinații de intrări.
Următorul tabel prezintă tabelul de stări al flip-flop-ului JK.
| J | K | Q(t + 1) | |
|---|---|---|---|
| 0 | 0 | 0 | Q(t) |
| 0 | 1 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 | Q(t)’ |
Aici, Q(t) & Q(t + 1) sunt starea prezentă & respectiv următoarea stare. Astfel, flip-flop-ul JK poate fi utilizat pentru una dintre aceste patru funcții, cum ar fi Hold, Reset, Set & Complementul & stării prezente în funcție de condițiile de intrare, atunci când se aplică tranziția pozitivă a semnalului de ceas. Tabelul următor prezintă tabelul caracteristic al flip-flopului JK.
| Intrări prezente | Stare prezentă | ||||
|---|---|---|---|---|---|
| J | K | Q(t) | Q(t+1) | ||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 1 | 1 | 0 | ||
| 1 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | 0 |
Cu ajutorul celor trei variabile K-Harta, putem obține expresia simplificată pentru următoarea stare, Q(t + 1). Harta K cu trei variabile pentru următoarea stare, Q(t + 1) este prezentată în figura următoare.
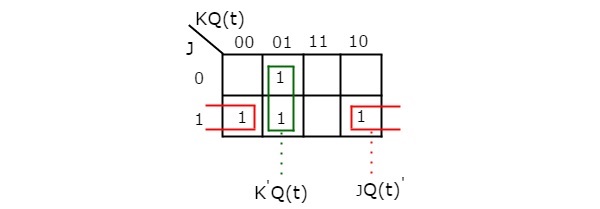
Grupările maxime posibile ale celor adiacente sunt deja prezentate în figură. Prin urmare, expresia simplificată pentru următoarea stare Q(t+1) este
$$Q\left ( t+1 \right )=J{{Q\left ( t \right )}’+{K}’Q\left ( t \right )$$
T Flip-Flop
T flip-flop este versiunea simplificată a flip-flop-ului JK. Se obține prin conectarea aceleiași intrări “T” la ambele intrări ale flip-flopului JK. Funcționează numai cu tranziții de ceas pozitive sau tranziții de ceas negative. Schema de circuit a flip-flop-ului T este prezentată în figura următoare.
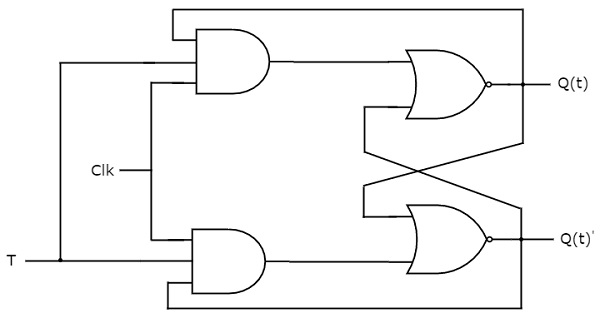
Acest circuit are o singură intrare T și două ieșiri Q(t) & Q(t)’. Funcționarea flip-flopului T este aceeași cu cea a flip-flopului JK. Aici, am considerat că intrările flip-flopului JK sunt J = T și K = T pentru a utiliza flip-flopul JK modificat pentru 2 combinații de intrări. Astfel, am eliminat celelalte două combinații de J & K, pentru care aceste două valori sunt complementare între ele în flip-flop T.
Următorul tabel prezintă tabelul de stări al flip-flopului T.
| D | Q(t + 1) |
|---|---|
| 0 | Q(t) |
| 1 | Q(t)’ |
Aici, Q(t) & Q(t + 1) sunt starea prezentă & respectiv următoarea stare. Astfel, flip-flop-ul T poate fi utilizat pentru una dintre aceste două funcții, cum ar fi Hold, & Complementul stării prezente în funcție de condițiile de intrare, atunci când se aplică tranziția pozitivă a semnalului de ceas. Tabelul următor prezintă tabelul caracteristic al flip-flop-ului T.
| Intrare | Stare prezentă | ||
|---|---|---|---|
| T | Q(t) | Q(t + 1) | |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
Din tabelul caracteristic de mai sus, putem scrie direct următoarea ecuație de stare sub forma
$$Q\stânga ( t+1 \dreapta )={T}’Q\stânga ( t \dreapta )+TQ{\stânga ( t \ dreapta )}’}’$$
$$$$$Rightarrow Q\left ( t+1 \ dreapta )=T\oplus Q\left ( t \ dreapta )$$
Lovitura lui T flip-flop se comută întotdeauna pentru fiecare tranziție pozitivă a semnalului de ceas, atunci când intrarea T rămâne la nivelul logic înalt (1). Prin urmare, flip-flop-ul T poate fi utilizat în contoare.
În acest capitol, am implementat diverse flip-flops prin asigurarea cuplării încrucișate între porțile NOR. În mod similar, puteți implementa aceste flip-flops utilizând porți NAND.
.