6.3 Rețele de credință
Noțiunea de independență condiționată poate fi folosită pentru a oferi o reprezentare concisă a multor domenii. Ideea este că, dată fiind o variabilă aleatorie X, poate exista un mic set de variabile careafectează direct valoarea variabilei, în sensul că X esteindependentă în mod condiționat de alte variabile, date fiind valorile variabilelor care o afectează direct. Setul de variabile care afectează local se numește pătură Markov. Această localitate este cea care este exploatată în cadrul unei rețele de credință. O rețea de convingeri este un model dirijat de dependență condiționată între un set de variabile aleatoare. Afirmația precisă a independenței condiționate într-o rețea de credință ia în considerare direcționalitatea.
Pentru a defini o rețea de credință, începeți cu un set de variabile aleatoare care reprezintă toate caracteristicile modelului. Să presupunem că aceste variabile sunt {X1,…,Xn}.Apoi, selectați o ordonare totală a variabilelor, X1,…,Xn.
Regula lanțului (Propoziția 6.3) arată cum se descompune o conjuncție în probabilități condiționate:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Sau, în termeni de variabile aleatoare și distribuții de probabilitate,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Definiți părinții variabilei aleatoare Xi, scrisparents(Xi), ca fiind un set aminimal de predecesori ai lui Xi în ordinea totală astfel încât ceilalți predecesori ai lui Xi să fie condițional independenți de Xi dat fiindparents(Xi). Adică, parents(Xi) ⊆{X1,…,Xi-1} astfel încât
P(Xi|Xi-1…X1) = P(Xi|parents(Xi)).
Dacă există mai mult de un set minimal, orice set minimal poate fi ales ca părinte. Poate exista mai mult de un set minimal doar atunci când unii dintre predecesori sunt funcții deterministe ale altora.
Pot fi puse împreună regula lanțului și definiția părinților,obținând
P(X1, X2,—, Xn) = ∏i=1n P(Xi|părinții(Xi)).
Probabilitatea asupra tuturor variabilelor, P(X1, X2,—,Xn), se numește distribuție de probabilitate comună. O rețea de credință definește o factorizare a distribuției de probabilitate comună, în care probabilitățile condiționate formează factori care sunt înmulțiți împreună.
O rețea de credință, numită și rețea bayesiană, este un graf aciclicdirecționat (DAG), în care nodurile sunt variabile aleatoare. Există un arc de la fiecare element dinparents(Xi) în Xi.Asociat cu rețeaua de credință este un set de distribuții de probabilități condiționate – probabilitatea condiționată a fiecărei variabile în funcție de părinții săi (care include probabilitățile anterioare ale acelor variabile fără părinți).
Astfel, o rețea de credință este formată din
- un DAG, în care fiecare nod este etichetat cu o variabilă aleatorie;
- un domeniu pentru fiecare variabilă aleatorie; și
- un set de distribuții de probabilitate condiționată care dau P(X|părinți(X)) pentru fiecare variabilă X.
O rețea de credință este aciclică prin construcție. Modul în care lanțul reglatcompune conjuncția dă ordinea. O variabilă poate avea ca părinți numai predecesori.Diferite descompuneri pot avea ca rezultat rețele de credință diferite.
Să presupunem că folosim următoarele variabile, care sunt toate booleene, în următoarea ordine:
- Alterarea este adevărată atunci când există o alterare a alarmei.
- Foc este adevărată atunci când există un incendiu.
- Alarmă este adevărată atunci când alarma sună.
- Fum este adevărată atunci când există fum.
- Plecare este adevărată dacă există mai multe persoane care părăsesc clădirea în același timp.
- Raport este adevărată dacă există un raport dat de cineva despre persoane care pleacă. Raport este fals dacă nu există nici un raport de plecare.
Variabila Raport denotă raportul senzorului că oamenii pleacă. Această informație nu este fiabilă, deoarece persoana care emite un astfel de raport ar putea face o glumă, sau este posibil ca nimeni care ar fi putut da un astfel de raport să nu fi fost atent. Această variabilă este introdusă pentru a permite condiționarea pe baza datelor nesigure ale senzorilor. Agentul știe ce raportează senzorul,dar nu dispune decât de dovezi nesigure cu privire la persoanele care părăsesc clădirea.Ca parte a domeniului, presupuneți următoarele independențe condiționate:
- Incendiul este condiționat independent de Tampering (în lipsa altor informații).
- Alarma depinde atât de Fire cât și de Tampering. Adică, nu facem nici o ipoteză de independență cu privire la modul în care alarma depinde de predecesoarele sale, având în vedere această ordine a variabilelor.
- Fumul depinde numai de incendiu și este condiționat independent de manipulare și de alarmă, având în vedere dacă există sau nu un incendiu.
- Plecarea depinde numai de alarmă și nu direct de incendiu sau de manipulare sau de fum. Adică, plecarea este condițional independentă de celelalte variabile dată fiind Alarma.
- Raportul depinde doar direct de Plecare.
Rețeaua de credință din Figura 6.1 exprimă aceste dependențe.
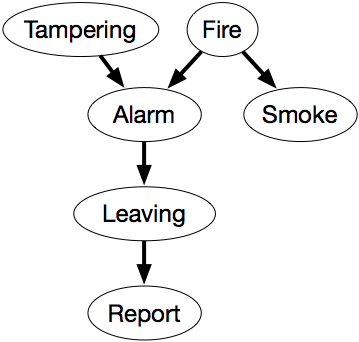
Această rețea reprezintă factorizarea
P(Tampering,Fire,Alarm,Smoke,Leaving,Raport) = P(Tampering) ×P(Fire) ×P(Alarm|Tampering,Fire) ×P(Smoke|Fire) ×P(Leaving|Alarm) ×P(Report|Leaving).
De asemenea, trebuie să definim domeniul fiecărei variabile. Să presupunem că variabilele sunt booleene; adică au domeniul {true,false}. Utilizăm varianta minusculă a variabilei pentru a reprezenta valoarea adevărată și utilizăm negația pentru valoarea falsă. Astfel, de exemplu, Tampering=adevărat se scrie ca tampering, iar Tampering=fals se scrie ca ¬tampering.
Exemplele care urmează presupun următoarele probabilități condiționate:
P(incendiu) = 0,01
P(alarmă | incendiu ∧ manipulare) = 0.5
P(alarmă | incendiu ∧¬manipulare) = 0,99
P(alarmă | ¬incendiu ∧¬manipulare) = 0,85
P(alarmă | ¬incendiu ∧¬manipulare) = 0,0001
P(fum | incendiu ) = 0.9
P(smoke | ¬fire ) = 0.01
P(leaving | alarmă) = 0.88
P(leaving | ¬alarmă ) = 0.001
P(report | leaving ) = 0.75
P(report | ¬leaving ) = 0.75
P(report | ¬leaving ) = 0.01
- Pentru fiecare fir wi, există o variabilă aleatoare, Wi, cu domeniul {live,dead}, care denotă dacă există energie în firul wi. Wi=live înseamnă că firulwi are putere. Wi=dead înseamnă că nu există curent în firul wi.
- Outside_power cu domeniul {live,dead} indică dacă există curent care intră în clădire.
- Pentru fiecare întrerupător si, variabila Si_pos indică poziția luisi. Ea are domeniul {up,down}.
- Pentru fiecare întrerupător si, variabila Si_st denotă starea întrerupătorului si. Are domeniul {ok,upside_down,short,intermittent,broken}. Si_st=ok înseamnă că întrerupătorul si funcționează normal. Si_st=întors cu susul în jos înseamnă că întrerupătorul si este instalat cu susul în jos. Si_st=short înseamnă că întrerupătorul si este scurtcircuitat și acționează ca un fir. Si_st=broken înseamnă că întrerupătorul si este rupt și nu permite trecerea electricității.
- Pentru fiecare întrerupător de circuitercbi, variabila Cbi_st are domeniul {on,off}. Cbi_st=on înseamnă că energia electrică poate trece prin cbi, iar Cbi_st=off înseamnă că energia electrică nu poate trece prin cbi.
- Pentru fiecare lumină li, variabila Li_st cu domeniul {ok,intermitent,întrerupt} indică starea luminii. Li_st=ok înseamnă că lumina li se va aprinde dacă este alimentată, Li_st=intermittent înseamnă că lumina li se aprinde intermitent dacă este alimentată, iar Li_st=broken înseamnă că lumina li nu funcționează.
Să selectăm o ordine în care cauzele unei variabile sunt înaintea variabilei în ordinea respectivă. De exemplu, variabila pentru a afla dacă o lumină este aprinsă vine după variabilele pentru a afla dacă lumina funcționează și dacă există curent electric care intră în lumină.
Dacă lumina l1 este aprinsă depinde doar de faptul dacă există curent în firul w0 și dacă lumina l1 funcționează corect. Alte variabile, cum ar fi poziția comutatorului s1, dacă lumina l2 este aprinsă sau cine este regina Canadei, sunt irelevante. Astfel, părinții lui L1_lit sunt W0 și L1_st.
Considerați variabila W0, care reprezintă dacă există curent în firul w0. Dacă am ști dacă există curent în firele w1 și w2 și am ști dacă poziția comutatorului s2 și dacă acesta funcționează corect, valoarea celorlalte variabile (altele decât L1_lit) nu ne-ar afecta convingerea că există curent în firul w0. Astfel, părinții lui W0 ar trebui să fie S2_Pos, S2_st,W1 și W2.
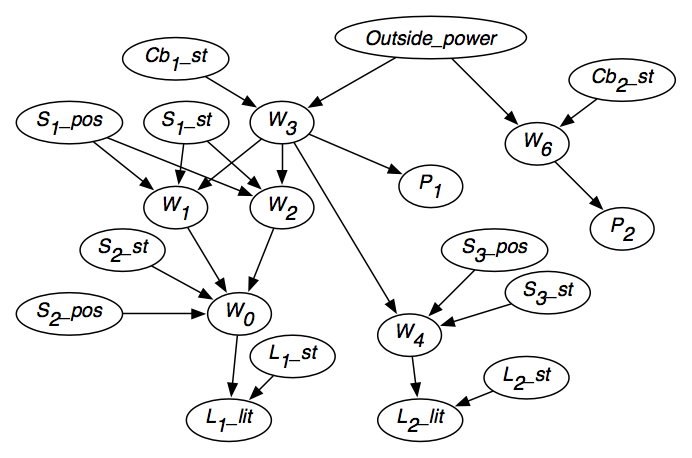
Figura 6.2 prezintă rețeaua de credință rezultată după ce a fost luată în considerare independența fiecărei variabile.Rețeaua de credință conține, de asemenea, domeniile variabilelor, așa cum sunt prezentate în figură, și probabilitățile condiționate ale fiecărei variabile având în vedere părinții săi.
Pentru variabila W1, trebuie specificate următoarele probabilități condiționate:
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=live)
P(W1=live|S1_pos=up ∧S1_st=ok ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=live|S1_pos=down ∧S1_st=broken ∧W3=dead).
Există două valori pentru S1_pos, cinci valori pentru S1_ok șidouă valori pentru W3, astfel încât există 2×5 ×2 = 20 de cazuri diferite în care trebuie specificată o valoare pentru W1=live. În ceea ce privește teoria probabilității, probabilitatea pentru W1=viață în aceste 20 de cazuri poate fi atribuită în mod arbitrar. Desigur, cunoașterea domeniului limitează valorile care au sens. Valorile pentruW1=mort pot fi calculate din valorile pentru W1=vii pentru fiecare dintre aceste cazuri.
Pentru că variabila S1_st nu are părinți, ea necesită o distribuție anterioară, care poate fi specificată ca probabilități pentru toate valorile, cu excepția uneia dintre ele; valoarea rămasă poate fi derivată din constrângerea ca toate probabilitățile să fie egale cu 1. Astfel, pentru a preciza distribuția lui S1_st, trebuie specificate patru din următoarele cinci probabilități:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
O rețea de credință este o reprezentare grafică a independenței condiționate.independența ne permite să reprezentăm efectele directe în cadrul grafuluiși prescrie ce probabilități trebuie specificate. Din rețea pot fi derivate probabilități posterioare arbitrare.
Ipoteza de independență încorporată într-o rețea de credință este următoarea: Fiecare variabilă aleatorie este condițional independentă față de cei care nu descind din ea, având în vedere părinții săi. Adică, dacă X este o variabilă aleatoare cu părinții Y1,…, Yn, toate variabilele aleatoare care nu sunt descendenți ai lui X sunt condițional independente de X dat fiind Y1,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
dacă R nu implică un descendent al lui X. Pentru această definiție, îl includem pe X ca fiind un descendent al său. Partea dreaptă a acestei ecuații este forma probabilităților care sunt specificate ca parte a rețelei de credință.R poate implica strămoși ai lui X și alte noduri atâta timp cât acestea nu sunt descendenți ai lui X. Ipoteza de independență afirmă că toată influența variabilelor care nu sunt descendenți este captată prin cunoașterea valorii părinților lui X.
De multe ori, ne referim doar la DAG-ul etichetat ca fiind o rețea de credință. Atunci când se face acest lucru, este important să ne amintim că un domeniu pentru fiecare variabilă și un set de distribuții de probabilitate condiționată fac, de asemenea, parte din rețea.
Numărul de probabilități care trebuie specificate pentru fiecare variabilă este exponențial în numărul de părinți ai variabilei.Ipoteza de independență este utilă în măsura în care numărul de variabile care afectează direct o altă variabilă este mic. Ar trebui să ordonați variabilele astfel încât nodurile să aibă cât mai puțini părinți posibil.
Rețelele de credință și cauzalitatea
Rețelele de credință au fost deseori numite rețele cauzale și s-a afirmat că sunt o bună reprezentare a cauzalității.Reamintim că un model cauzal prezice rezultatul intervențiilor.Să presupunem că aveți în minte un model cauzal al unui domeniu, în care domeniul este specificat în termeni de un set de variabile aleatoare. Pentru fiecare pereche de variabile aleatoare X1și X2, dacă există o legătură cauzală directă de la X1 la X2 (adică, intervenția pentru a schimba X1 într-un anumit context de alte variabile afectează X2 și acest lucru nu poate fi modelat prin existența unei variabile de intervenție), adăugați un arc de laX1 la X2. V-ați aștepta ca modelul cauzal să respecte ipoteza de independență a rețelei de credințe. Astfel, toateconcluziile rețelei de credințe ar fi valabile.
Vă așteptați, de asemenea, ca un astfel de graf să fie aciclic; nu vreți ca ceva să se cauzeze pe sine în cele din urmă. Această ipoteză este rezonabilă dacă luați în considerare faptul că variabilele aleatoare reprezintă evenimente particulare mai degrabă decât tipuri de evenimente. De exemplu, luați în considerare un lanț cauzal conform căruia “a fi stresat” vă determină să “lucrați ineficient”, care, la rândul său, vă determină să “fiți stresat”. Pentru a rupe ciclul aparent, putem reprezenta “a fi stresat” în diferite etape ca variabile aleatoare diferite care se referă la momente diferite. Faptul că ați fost stresat în trecut vă face să nu lucrați bine în acest moment, ceea ce vă face să fiți stresat în viitor. Variabilele ar trebui să satisfacă principiul clarității și să aibă un înțeles bine definit. Variabilele nu ar trebui să fie văzute ca tipuri de evenimente.
Rețeaua de credințe în sine nu are nimic de spus despre cauzalitate și poate reprezenta independența non-causală, dar pare deosebit de adecvată atunci când există cauzalitate într-un domeniu. Adăugarea de arce care reprezintă cauzalitatea locală tinde să producă o rețea de credință mică. Rețeaua de credință dinFigura 6.2 arată cum se poate realiza acest lucru pentru un domeniu simplu.
Intervențiile modelelor de rețele cauzale. Dacă cineva ar forța în mod artificial o variabilă să aibă o anumită valoare, descendenții variabilei – dar nu și alte noduri – ar fi afectați. În cele din urmă, puteți vedea modul în care cauzalitatea din rețelele de credință se leagă de raționamentul cauzal și probatoriu discutat înSecțiunea 5.7. O rețea de credințe cauzală poate fi văzută ca fiind o îndepărtare a axiomatizării într-o direcție cauzală. Raționamentul în rețelele de credințecorespunde la abducția la cauze și apoi la predicția din acestea. Există o corespondență directă între punctul de vedere logicabductiv discutat în secțiunea 5.7 și rețelele de credințe: Rețelele de convingeri pot fi modelate ca programe logice cu probabilități asupra ipotezelor posibile. Acest lucru este descris în secțiunea 14.3.
Rețineți restricția “fiecare variabilă aleatorie este condițional independentă față de non-descendentele sale, având în vedere părinții săi” în definiția independenței codificate într-o rețea de credințe. DacăR conține un descendent al variabilei X, ipoteza de independență nu se aplică în mod direct.
Variabila S1_pos nu are părinți. Astfel, independența încorporată în rețeaua de credință specifică faptul că P(S1_pos=up|A) =P(S1_pos=up) pentru orice A care nu implică un descendent al luiS1_pos. Dacă A include un descendent al lui S1_pos=up – de exemplu, dacă A este S2_pos=up∧L1_lit=adevărat – ipoteza de independență nu poate fi aplicată direct.
Această rețea poate fi utilizată în mai multe moduri:
- Prin condiționarea de cunoașterea faptului că întrerupătoarele și întrerupătoarele sunt în regulă, precum și de valorile puterii exterioare și de poziția întrerupătoarelor, această rețea poate simula modul în care ar trebui să funcționeze iluminatul.
- Date fiind valorile puterii exterioare și poziția întrerupătoarelor, rețeaua poate deduce probabilitatea oricărui rezultat – de exemplu, cât de probabil este ca l1 să fie aprins.
- Date valorile pentru întrerupătoare și dacă luminile sunt aprinse,se poate deduce probabilitatea posterioară ca fiecare întrerupător sau întrerupător de circuit să se afle într-o anumită stare.
- Date unele observații, rețeaua poate fi utilizată pentru a raționa invers pentru a determina poziția cea mai probabilă a întrerupătoarelor.
- Datorită unor poziții ale comutatorului, unor ieșiri și unor valori intermediare, rețeaua poate fi utilizată pentru a determina probabilitatea oricărei alte variabile din rețea.
O rețea de credință specifică o distribuție comună de probabilitate din care pot fi derivate probabilități condiționate arbitrare. O rețea poate fi interogată prin solicitarea probabilității condiționate a oricărei variabile condiționate de valorile oricăror alte variabile. Acest lucru se face în mod obișnuit prin furnizarea de observații asupra unor variabile și prin interogarea unei alte variabile.
P(incendiu) = 0,01
P(raport ) = 0,028
P(fum) = 0.0189
Observând raportul rezultă următoarele:
P(incendiu |raport)= 0,2305
P(fum |raport) = 0,215
Cum era de așteptat, probabilitatea atât a manipulării cât și a incendiului sunt crescute de raport. Deoarece incendiul este crescut, la fel este și probabilitatea de fum.
Să presupunem în schimb că s-a observat fum:
P(incendiu|fum) = 0,476
P(raport |fum) = 0,320
Rețineți că probabilitatea de manipulare nu este afectată de observarea fumului; cu toate acestea, probabilitățile de raport și de incendiu sunt crescute.
Să presupunem că au fost observate atât raportarea cât și fumul:
P(incendiu |raport ∧fum) = 0,964
Observarea ambelor face ca incendiul să fie și mai probabil. Cu toate acestea, încontextul raportului, prezența fumului face ca falsificarea să fie mai puțin probabilă. Acest lucru se datorează faptului că raportul este explicat prin incendiu, care este acum mai probabil.
Să presupunem în schimb că s-a observat raportul, dar nu și fumul:
P(incendiu|raport ∧¬fum) = 0,0294
În contextul raportului, incendiul devine mult mai puțin probabil și astfel crește probabilitatea de manipulare pentru a explica raportul.
Acest exemplu ilustrează modul în care ipoteza de independență a rețelei de credință oferă concluzii comune și, de asemenea, demonstrează cum explicarea este o consecință a ipotezei de independență a unei rețele de credință.
- 6.3.1 Construirea rețelelor de credință