Testul Kolmogorov-Smirnov
Testul K-S este un test de adecvare utilizat pentru a evalua uniformitatea unui set de distribuții de date. A fost conceput ca răspuns la neajunsurile testului chi pătrat, care produce rezultate precise doar pentru distribuții discrete, cu binomuri. Testul K-S are avantajul de a nu face nicio presupunere cu privire la clasificarea seturilor de date care urmează să fie comparate, eliminând caracterul arbitrar și pierderea de informații care însoțește procesul de selecție a clasificării.
În statistică, testul K-S este testul acceptat pentru măsurarea diferențelor dintre seturile de date continue (distribuții de date nebinate) care sunt o funcție a unei singure variabile. Această măsură a diferenței, statistica K-S \(D\), este definită ca fiind valoarea maximă a diferenței absolute dintre două funcții de distribuție cumulativă. Testul K-S unilateral este utilizat pentru a compara un set de date cu o funcție de distribuție cumulativă cunoscută, în timp ce testul K-S bilateral compară două seturi de date diferite. Fiecare set de date oferă o funcție de distribuție cumulativă diferită, iar semnificația acesteia rezidă în relația sa cu distribuția de probabilitate din care este extras setul de date: funcția de distribuție a probabilității pentru o singură variabilă independentă \(x\) este o funcție care atribuie o probabilitate fiecărei valori de \(x\). Probabilitatea asumată de valoarea specifică \(x_{i}\) este valoarea funcției de distribuție a probabilității la \(x_{i}\) și este notată \(P(x_{i})\).Funcția de distribuție cumulativă este definită ca fiind funcția care indică fracțiunea de puncte de date aflate la stânga unei valori date \(x_{i}\), \(P(x <x_{i})\); aceasta reprezintă probabilitatea ca \(x\) să fie mai mică sau egală cu o anumită valoare \(x_{i}\).
Astfel, pentru compararea a două funcții de distribuție cumulativă diferite \(S_{N1}(x)\) și \(S_{N2}(x)\), statistica K-S este
D = max|S_N1(x) – S_N2(x)|
unde \(S_{N}(x)\) este funcția de distribuție cumulativă a distribuției de probabilități din care este extras un set de date cu \(N\) evenimente. Dacă evenimentele ordonate \(N\) sunt localizate în punctele de date \(x_{i}\), unde \(i = 1, \lpuncte, N\), atunci
S_N(x_i) = (i-N)/N
unde matricea de date \(x\) este ordonată în ordine crescătoare. Aceasta este o funcție în trepte care crește cu \(1/N\) la valoarea fiecărui punct de date ordonat.
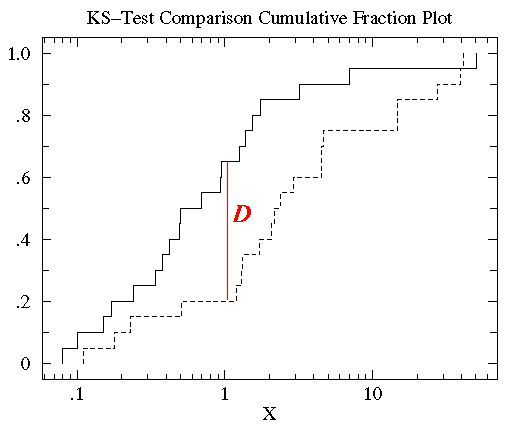
Kirkman, T.W. (1996) Statistici la îndemână.
http://www.physics.csbsju.edu/stats/
În scopul nostru, cele două distribuții comparate sunt distribuția măsurată a timpilor de sosire și fracția acumulată pe intervalul de timp scurs. Dacă ipoteza nulă (fără variabilitate) este valabilă, obținem 50% din evenimente în 50% din timpul scurs, iar statistica \(D\) ar trebui să se distribuie în conformitate cu distribuția Kolmogorov pentru multe realizări ale distribuției timpilor de sosire. Probabilitatea returnată de test este astfel \(p_{KS} = 1 – \alpha\), unde \(\alpha\) este probabilitatea (conform distribuției Kolmogorov) ca valoarea lui \(D\) să fie mai mare sau egală cu valoarea măsurată. Prin urmare, o valoare mică a lui \(p_{KS}\) indică o concordanță cu ipoteza nulă, în timp ce o valoare mare a lui \(p_{KS}\) indică faptul că intervalul dintre evenimente nu este constant și, prin urmare, poate fi dedusă variabilitatea.