Tetraedru

Contenutul acestei pagini Ce este un tetraedru? Piese ale tetraedrului Numerele tetraedrice Tetraedrul în cub Inele de tetraedre Tetraedre peInternet

La pagina principală “Mathematische Basteleien”

Ce este un tetraedru?

Un tetraedru este o figură tridimensională cu patru triunghiuri echilaterale. Dacă ridicați trei triunghiuri (1), veți obține tetraedrulîn vedere de sus (2). În general, el este prezentat în perspectivă (3).

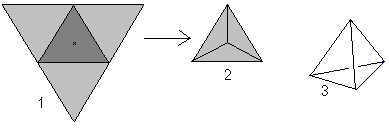
Dacă vă uitați la cuvântul tetraedru (tetraedru înseamnă “cu patru planuri”), ați putea numi tetraedru orice piramidă cu un triunghi ca bază.

Cu toate acestea, tetraedrul este piramida triunghiulară dreaptă și regulată de pe acest site.

Pietre din vârfulTetraedrului
Înălțimea și aria unui triunghi lateral
Cele patru triunghiuri echilaterale formează un tetraedru.

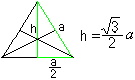…	Se alege un triunghi: Cele trei înălțimi se intersecteazăîntr-un punct ca în orice triunghi. Acesta este centrul triunghiului. Înălțimea poate fi calculată în funcție de latura a sub forma h=sqr(3)/2*a folosind teorema lui Pitagora.

Înălțimile sunt de asemenea mediane și se intersectează cu raportul2:1. Acesta este folosit în calculele următoare.

Aria triunghiului este A=sqr(3)/4*a².

Înălțimea spațiului

Înălțimea tetraedrului este cuprinsă între centrul triunghiului de bază (1) și vârful (2). Pentru calcule se ia în considerare așa-numitul triunghi de sprijin (3, galben), care este format de o muchie și două înălțimi de triunghi. Există H=sqr(6)/3*a folosind teorema lui Pitagora.
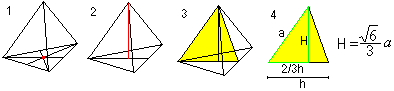
Centru, sferă circumscrisă și sferă înscrisă Centrul unui tetraedru este intersecția a două înălțimi de spațiu (1,2,3). Este centrul de greutate, centrul sferei prin cele patru colțuri și centrul celei mai mari sfere, care încă mai încape în interiorul tetraedrului (4).

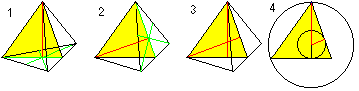
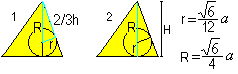…	Se obțin două formule pentru r și R cu ajutorul teoremei lui Pitagora (1) și H=R+r (2): Există r=sqr(6)/12*a , R=sqr(6)/4*a.

Suprafața unghiulară

….…..

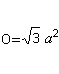Aria bazei și a fețelor laterale formează suprafațaO. Există O=4*4*A (triunghi) = sqr(3)a².

Volum

Numerele tetraedrice top

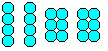……	Dacă lipiți 20 de bile în două grupe cu patru și două cu șase, obțineți un puzzle bine cunoscut: Trebuie să formați o piramidă cu patru piese.

Există multe puzzle-uri similare.

Tetraedru în cubul de sus
Cele șase diagonale ale fețelor formează un tetraedru în cub.
Dacă cunoașteți vederea 3D, puteți privi tridimensional următoarele două perechi de cuburi.

Volumul tetraedrului este a treia parte din volumul cubului.

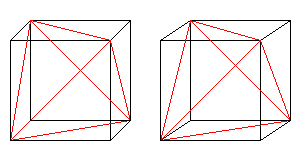
Dacă desenați un al doilea tetraedru și liniile de intersecție,obțineți o penetrare a două tetraedre.

Figura este formată din diagonalele fețelor și liniile de legătură ale centrelor pătratelor laterale ale cubului inițial. Ultimeletone formează un octaedru.

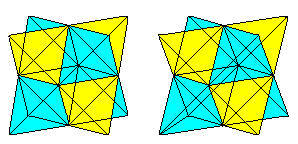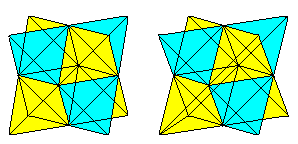
Înele de tetraedre top
Puteți confecționa tetraedre de hârtie și lipi un număr parde ele pe un inel. Inelul se poate răsuci continuu spre interior sau spre exterior prin centru. Aceasta este o jucărie drăguță. – Aceste inele se mai numesc și kaleidocicluri.găsiți mai multe pe pagina mea web Kaleidocicluri.

Tetraedrepe Internettop

German

Christof Weber
Washat dieser Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)

Albert Kluge
Einrotierender Tetraeder als Java-Applet

FAZ
Tetraederpackung:Eins geht noch

Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)

Gerd Müller
PlatonischeKörper in Stereodarstellung

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder

ruhr-guide
TetraederBottrop

Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl

Engleză

Eric W. Weisstein (World of Mathematics)
Tetrahedron

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetrahedron

Joyce Frost și Peg Cagle (mathforum)
Un tetraedru neregular, uimitor, care umple spațiul

Wikipedia
Tetrahedron,Tetrapod(structură), Tetrahedralnumber

.