Gráficos en Python

Orígenes de la teoría de grafos

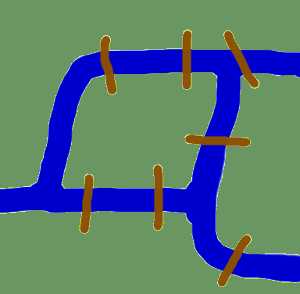Antes de empezar con las implementaciones reales de grafos en Python y antes de empezar con la introducción de los módulos de Python que tratan con grafos, queremos dedicarnos a los orígenes de la teoría de grafos.
Los orígenes nos llevan a la Künigsberg del siglo XVIII. Königsberg era entonces una ciudad de Prusia. El río Pregel atravesaba la ciudad, creando dos islas. La ciudad y las islas estaban conectadas por siete puentes, como se muestra. Los habitantes de la ciudad se preguntaban si era posible dar un paseo por la ciudad visitando cada zona de la misma y cruzando cada puente una sola vez. Cada puente debe ser cruzado completamente, es decir, no está permitido caminar hasta la mitad de un puente y luego dar la vuelta y cruzar más tarde la otra mitad desde el otro lado. Leonhard Euler resolvió el problema en 1735 demostrando que no es posible. Descubrió que la elección de un recorrido dentro de cada terreno es irrelevante y que lo único que importaba era el orden (o la secuencia) en que se cruzan los puentes. Formuló una abstracción del problema, eliminando los hechos innecesarios y centrándose en las zonas terrestres y los puentes que las conectan. De este modo, creó los fundamentos de la teoría de los grafos. Si vemos una “zona de tierra” como un vértice y cada puente como una arista, hemos “reducido” el problema a un grafo.

Introducción a la teoría de grafos usando Python

Antes de comenzar nuestro tratado sobre posibles representaciones de grafos en Python, queremos presentar algunas definiciones generales de los grafos y sus componentes.
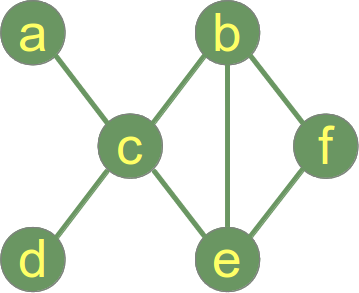
Un “grafo “1 en matemáticas y ciencias de la computación está formado por “nodos”, también conocidos como “vértices”.Los nodos pueden o no estar conectados entre sí. En nuestra ilustración, que es una representación pictórica de un grafo, el nodo “a” está conectado con el nodo “c”, pero “a” no está conectado con “b”. La línea de conexión entre dos nodos se llama arista. Si las aristas entre los nodos no están dirigidas, el grafo se denomina grafo no dirigido. Si una arista está dirigida de un vértice (nodo) a otro, el grafo se denomina grafo dirigido. Una arista dirigida se llama arco.
Aunque los grafos pueden parecer muy teóricos, muchos problemas prácticos pueden representarse mediante grafos. Se utilizan a menudo para modelar problemas o situaciones en física, biología, psicología y, sobre todo, en informática. En informática, los grafos se utilizan para representar redes de comunicación, organización de datos, dispositivos computacionales, el flujo de la computación,

En este último caso, se utilizan para representar la organización de los datos, como el sistema de archivos de un sistema operativo, o las redes de comunicación. La estructura de enlaces de los sitios web también puede verse como un grafo, es decir, un grafo dirigido, porque un enlace es una arista o un arco dirigido.
Python no tiene ningún tipo o clase de datos incorporado para los grafos, pero es fácil implementarlos en Python. Un tipo de datos es ideal para representar grafos en Python, es decir, los diccionarios. El grafo de nuestra ilustración se puede implementar de la siguiente manera:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Las claves del diccionario anterior son los nodos de nuestro grafo. Los valores correspondientes son listas con los nodos, que se conectan mediante una arista. No hay forma más sencilla y elegante de representar un grafo.
Una arista puede verse como una 2-tupla con nodos como elementos, es decir (“a”, “b”)
Función para generar la lista de todas las aristas:Este código genera la siguiente salida, si se combina con el diccionario del grafo previamente definido:

 $ python3 graph_simple.py 

Como podemos ver, no hay ninguna arista que contenga el nodo “f”. “f” es un nodo aislado de nuestro grafo.
La siguiente función de Python calcula los nodos aislados de un grafo dado:Si llamamos a esta función con nuestro grafo, se devolverá una lista que contiene “f”:

Gráficos como clase de Python

Antes de continuar con la escritura de funciones para gráficos, tenemos un primer intento de implementación de una clase de gráficos de Python. Si miras el siguiente listado de nuestra clase, puedes ver en el método __init__ que utilizamos un diccionario “self.__graph_dict” para almacenar los vértices y sus correspondientes vértices adyacentes.
Si inicias este módulo de forma autónoma, obtendrás el siguiente resultado:

Caminos en Grafos

Queremos encontrar ahora el camino más corto de un nodo a otro nodo. Antes de pasar al código Python para este problema, tendremos que presentar algunas definiciones formales.
Vértices adyacentes:
Dos vértices son adyacentes cuando ambos inciden en una arista común.
Camino en un grafo no dirigido:
Un camino en un grafo no dirigido es una secuencia de vértices P = ( v1, v2, …., vn ) ∈ V x V x … x V tal que vi es adyacente a v{i+1} para 1 ≤ i < n. Tal camino P se denomina camino de longitud n desde v1 hasta vn.
Ruta simple:
Un camino sin vértices repetidos se denomina camino simple.
Ejemplo:
(a, c, e) es un camino simple en nuestro grafo, así como (a,c,e,b). (a,c,e,b,c,d) es un camino pero no un camino simple, porque el nodo c aparece dos veces.

El siguiente método encuentra un camino desde un vértice inicial hasta un vértice final:Si guardamos nuestra clase de grafos incluyendo el método encontrar_camino como “grafos.py”, podemos comprobar la forma de trabajar de nuestra función encontrar_camino:El resultado del programa anterior tiene este aspecto:
El método encontrar_todos_los_caminos encuentra todos los caminos entre un vértice inicial a un vértice final:Cambiamos ligeramente nuestro grafo de ejemplo añadiendo aristas de “a” a “f” y de “f” a “d” para probar el método previamente definido:El resultado tiene el siguiente aspecto:

Grado

El grado de un vértice v en un grafo es el número de aristas que lo conectan, contando los bucles dos veces. El grado de un vértice v se denota deg(v). El grado máximo de un grafo G, denotado por Δ(G), y el grado mínimo de un grafo, denotado por δ(G), son el grado máximo y mínimo de sus vértices.
En el grafo de la derecha, el grado máximo es 5 en el vértice c y el grado mínimo es 0, es decir, el vértice aislado f.
Si todos los grados de un grafo son iguales, el grafo es un grafo regular.En un grafo regular, todos los grados son iguales, y por tanto podemos hablar del grado del grafo.
La fórmula de la suma de grados (lema de Handshaking):
∑v &in; Vdeg(v) = 2 |E|
Esto significa que la suma de grados de todos los vértices es igual al número de aristas multiplicado por 2.Podemos concluir que el número de vértices con grado impar tiene que ser par. Esta afirmación se conoce como el lema del apretón de manos. El nombre “lema del apretón de manos” proviene de un problema matemático popular: En cualquier grupo de personas el número de personas que han estrechado la mano a un número impar de otras personas del grupo es par.
El siguiente método calcula el grado de un vértice:
El siguiente método calcula una lista que contiene los vértices aislados de un grafo:Los métodos delta y Delta se pueden utilizar para calcular el grado mínimo y máximo de un vértice respectivamente:

Secuencia de grados

La secuencia de grados de un grafo no dirigido se define como la secuencia de los grados de sus vértices en un orden no creciente.
El siguiente método devuelve una tupla con la secuencia de grados del grafo instancia:
La secuencia de grados de nuestro grafo ejemplo es la siguiente secuencia de enteros: (5,2,1,1,1,0).
Los grafos isomorfos tienen la misma secuencia de grados. Sin embargo, dos grafos con la misma secuencia de grados no son necesariamente isomorfos.
Se plantea la cuestión de si una secuencia de grados dada puede ser realizada por un grafo simple. El teorema de Erdös-Gallai afirma que una secuencia no creciente de n números di (parai = 1, …, n) es la secuencia de grados de un grafo simple si y sólo si la suma de la secuencia es par y se cumple la siguiente condición:

Implementación del teorema de Erdös-Gallai

Nuestra clase de grafos -véase más abajo la lista completa- contiene un método “erdoes_gallai” que decide si una secuencia cumple el teorema de Erdös-Gallai. Primero se comprueba si la suma de los elementos de la secuencia es impar. Si es así la función devuelve False, porque el teorema de Erdös-Gallai ya no se puede cumplir. Después comprobamos con el método estático is_degree_sequence si la secuencia de entrada es una secuencia de grado, es decir, que los elementos de la secuencia son no crecientes. Esto es un poco superfluo, ya que se supone que la entrada es una secuencia de grados, así que puedes eliminar esta comprobación por eficiencia. Ahora, comprobamos en el cuerpo de la segunda sentencia if, si se cumple la inecuación del teorema:
Versión sin la prueba superflua de la secuencia de grados:

Densidad del grafo

La densidad del grafo se define como el cociente entre el número de aristas de un grafo dado, y el número total de aristas, que podría tener el grafo. En otras palabras: Mide lo cerca que está un grafo dado de un grafo completo.
La densidad máxima es 1, si un grafo es completo. Esto está claro, porque el número máximo de aristas de un grafo depende de los vértices y se puede calcular como:
número máximo de aristas = ½ * |V| * ( |V| – 1 ).
Por otro lado, la densidad mínima es 0, si el grafo no tiene aristas, es decir, es un grafo aislado.
Para grafos simples no dirigidos, la densidad del grafo se define como: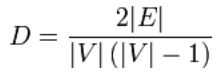

Un grafo denso es un grafo en el que el número de aristas es cercano al número máximo de aristas. Un grafo con pocas aristas se denomina grafo disperso. La definición de estos dos términos no es muy nítida, es decir, no existe un límite superior (supremum) para una densidad dispersa ni un límite inferior (infimum) para definir un grafo denso.
La notación matemática más precisa utiliza la notación big O:
Grafo disperso:
Gráfico denso:
Un grafo denso es un grafo G = (V, E) en el que |E| = Θ(|V|2).
“densidad” es un método de nuestra clase para calcular la densidad de un grafo:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Podemos probar este método con el siguiente script. Un grafo completo tiene una densidad de 1 y un grafo aislado tiene una densidad de 0, como podemos ver en los resultados del script de prueba anterior:

$ python test_density.py 0.4666666666671.00.0

Grafos conectados

Se dice que un grafo está conectado si cada par de vértices del grafo está conectado. El grafo de ejemplo de la derecha es un grafo conexo.

Es posible determinar con un sencillo algoritmo si un grafo es conexo:

1. Elegir un nodo arbitrario x del grafo G como punto de partida
2. Determinar el conjunto A de todos los nodos a los que se puede llegar desde x.
3. Si A es igual al conjunto de nodos de G, el grafo es conectado; en caso contrario, es desconectado.

Implementamos un método es_conectado para comprobar si un grafo es un grafo conectado. No ponemos énfasis en la eficiencia sino en la legibilidad.
Si se añade este método a nuestra clase grafo, podemos probarlo con el siguiente script. Suponiendo que guardas la clase graph como graph2.py:
Un componente conexo es un subgrafo conexo máximo de G. Cada vértice pertenece exactamente a un componente conexo, al igual que cada arista.

Distancia y diámetro de un grafo

La distancia “dist” entre dos vértices de un grafo es la longitud del camino más corto entre estos vértices. No se permiten retrocesos, desvíos o bucles para el cálculo de una distancia.
En nuestro gráfico de ejemplo de la derecha, la distancia entre el vértice a y el vértice f es 3, es decir, dist(a,f) = 3, porque el camino más corto pasa por los vértices c y e (o c y b alternativamente).
La excentricidad de un vértice s de un grafo g es la máxima distancia a cualquier otro vértice del grafo:
e(s) = max( { dist(s,v) | v ∈ V })
(V es el conjunto de todos los vértices de g)
El diámetro d de un grafo se define como la máxima excentricidad de cualquier vértice del grafo. Esto significa que el diámetro es la longitud del camino más corto entre los nodos más distanciados. Para determinar el diámetro de un grafo, primero hay que encontrar el camino más corto entre cada par de vértices. La mayor longitud de cualquiera de estos caminos es el diámetro del grafo.
Podemos ver directamente en nuestro grafo de ejemplo que el diámetro es 3, porque la longitud mínima entre a y f es 3 y no hay ningún otro par de vértices con un camino más largo.
El siguiente método implementa un algoritmo para calcular el diámetro. Podemos calcular el diámetro de nuestro grafo de ejemplo con el siguiente script, suponiendo de nuevo, que nuestra clase de grafos completa se guarda como graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Imprimirá el valor 3.

La clase de grafos de Python completa

En el siguiente código de Python, se encuentra el módulo de clase de Python completo con todos los métodos comentados:graph2.py

Árbol / Bosque

Un árbol es un grafo no dirigido que no contiene ciclos. Esto significa que dos vértices cualesquiera del grafo están conectados por exactamente un camino simple.

Un bosque es una unión disjunta de árboles. A diferencia de los bosques en la naturaleza, un bosque en la teoría de grafos puede consistir en un solo árbol.
Un grafo con un vértice y ninguna arista es un árbol (y un bosque).
Un ejemplo de árbol: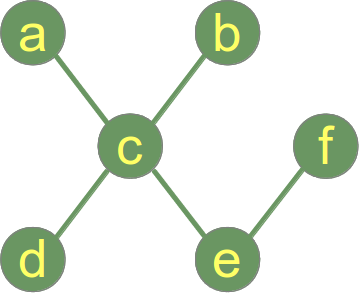

Mientras que el ejemplo anterior representa un grafo que es un árbol y un bosque, la siguiente imagen muestra un grafo que consiste en dos árboles, es decir, el grafo es un bosque pero no un árbol.es decir, el grafo es un bosque pero no un árbol:

Resumen de bosques:

Con un vértice:

Grafos de bosques con dos vértices:

Gráficos de bosques con tres vértices:

Árbol de expansión

Un árbol de expansión T de un grafo conexo y no dirigido G es un subgrafo G’ de G, que es un árbol,y G’ contiene todos los vértices y un subconjunto de las aristas de G. G’ contiene todas las aristas de G, si G es un grafo árbol. Informalmente, un árbol de expansión de G es una selección de aristas de G que forman un árbol que abarca todos los vértices. Es decir, cada vértice se encuentra en el árbol, pero no contiene ciclos (o bucles).
Ejemplo:
Un gráfico completamente conectado: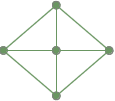

Dos árboles de expansión del gráfico completamente conectado anterior: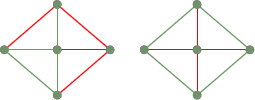

Juego Hamiltoniano

Un camino Hamiltoniano es un camino en un grafo no dirigido o dirigido que visita cada vértice exactamente una vez. Un ciclo (o circuito) hamiltoniano es un camino hamiltoniano que es un ciclo.
Nota para los informáticos: Generalmente, no es posible determinar, si tales caminos o ciclos existen en grafos arbitrarios, porque se ha demostrado que el problema del camino hamiltoniano es NP-completo.
Se llama así por William Rowan Hamilton, quien inventó el llamado “juego icosiano”, o rompecabezas de Hamilton, que consiste en encontrar un ciclo hamiltoniano en el grafo de aristas del dodecaedro. Hamilton resolvió este problema utilizando el cálculo icosiano, una estructura algebraica basada en raíces de la unidad con muchas similitudes con los cuaterniones, que también inventó.

Listado completo de la clase Graph

Podemos probar esta clase Graph con el siguiente programa:Si iniciamos este programa, obtendremos la siguiente salida:
Notas de pie de página:
1 Los grafos estudiados en la teoría de grafos (y en este capítulo de nuestro tutorial de Python) no deben confundirse con los grafos de las funciones
2 Un singleton es un conjunto que contiene exactamente un elemento.
Créditos:
Narayana Chikkam, nchikkam(at)gmail(dot)com, nos ha señalado un error de índice en el método “erdoes_gallai”. Muchas gracias, Narayana.