En el capítulo anterior, hablamos de los Latches. Estos son los bloques básicos de construcción de los flip-flops. Podemos implementar los flip-flops en dos métodos.
En el primer método, se conectan en cascada dos latches de tal manera que el primer latch se habilita para cada pulso de reloj positivo y el segundo latch se habilita para cada pulso de reloj negativo. Así, la combinación de estos dos latches se convierte en un flip-flop.
En el segundo método, podemos implementar directamente el flip-flop, que es sensible al flanco. En este capítulo, vamos a discutir los siguientes flip-flops utilizando el segundo método.
- SR Flip-Flop
- D Flip-Flop
- JK Flip-Flop
- T Flip-Flop
SR Flip-Flop
SR flip-flop opera sólo con transiciones de reloj positivas o negativas. En cambio, el latch SR funciona con la señal de habilitación. El diagrama del circuito del flip-flop SR se muestra en la siguiente figura.
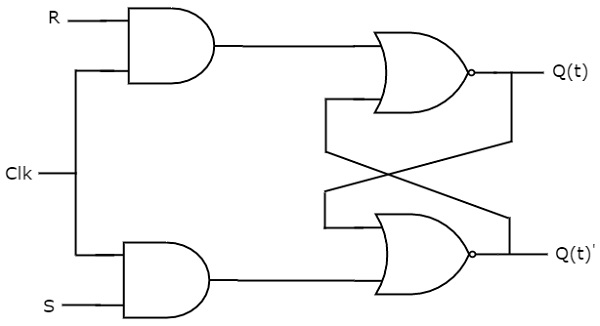
Este circuito tiene dos entradas S & R y dos salidas Q(t) & Q(t)’. El funcionamiento del flipflop SR es similar al SR Latch. Pero, este flip-flop afecta a las salidas sólo cuando se aplica la transición positiva de la señal de reloj en lugar de la habilitación activa.
La siguiente tabla muestra la tabla de estados del flip-flop SR.
| S | R | Q(t + 1) |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | – |
Aquí, Q(t) & Q(t + 1) son el estado actual & el siguiente estado respectivamente. Así, el flip-flop SR puede ser utilizado para una de estas tres funciones como Hold, Reset & Set basado en las condiciones de entrada, cuando se aplica la transición positiva de la señal de reloj. La siguiente tabla muestra la tabla de características del flip-flop SR.
| Entradas actuales | Estado actual | Estado siguiente | |
|---|---|---|---|
| S | R | Q(t) | Q(t + 1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | x |
| 1 | 1 | 1 | x |
Al utilizar tres variables K-Map, podemos obtener la expresión simplificada para el siguiente estado, Q(t + 1). El K-Map de tres variables para el siguiente estado, Q(t + 1) se muestra en la siguiente figura.
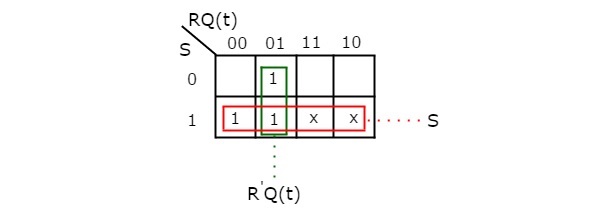
Las agrupaciones máximas posibles de adyacentes ya se muestran en la figura. Por tanto, la expresión simplificada para el siguiente estado Q(t + 1) es
$Q\left ( t+1 \right )=S+{R}’Q\left ( t \right )$
D Flip-Flop
D flip-flop opera sólo con transiciones de reloj positivas o transiciones de reloj negativas. Mientras que el latch D funciona con la señal de habilitación. Esto significa que la salida del flip-flop D es insensible a los cambios en la entrada, D excepto para la transición activa de la señal de reloj. El diagrama del circuito del flip-flop D se muestra en la siguiente figura.
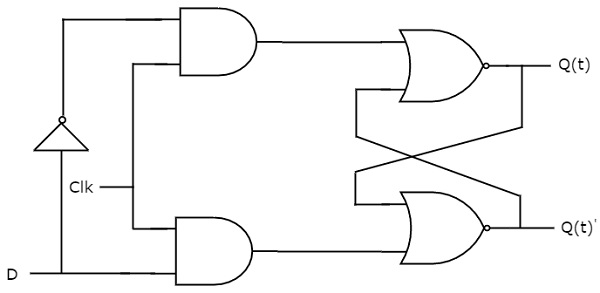
Este circuito tiene una sola entrada D y dos salidas Q(t) & Q(t)’. El funcionamiento del flip-flop D es similar al D Latch. Pero, este flip-flop afecta a las salidas sólo cuando se aplica la transición positiva de la señal de reloj en lugar de la habilitación activa.
La siguiente tabla muestra la tabla de estados del flip-flop D.
| D | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Por lo tanto, El flip-flop D siempre mantiene la información, que está disponible en la entrada de datos, D de la transición positiva anterior de la señal de reloj. A partir de la tabla de estados anterior, podemos escribir directamente la ecuación del siguiente estado como
Q(t + 1) = D
El siguiente estado del flip-flop D es siempre igual a la entrada de datos, D para cada transición positiva de la señal de reloj. Por lo tanto, los flip-flop D se pueden utilizar en registros, registros de desplazamiento y algunos de los contadores.
JK Flip-Flop
JK flip-flop es la versión modificada de SR flip-flop. Funciona sólo con transiciones de reloj positivas o transiciones de reloj negativas. El diagrama del circuito del flip-flop JK se muestra en la siguiente figura.
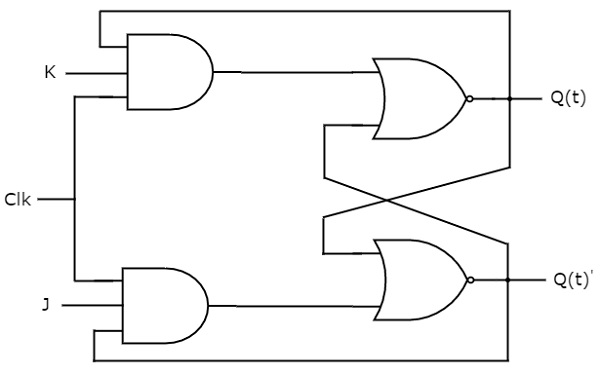
Este circuito tiene dos entradas J & K y dos salidas Q(t) & Q(t)’. El funcionamiento del flip-flop JK es similar al flip-flop SR. Aquí, consideramos las entradas del flip-flop SR como S = J Q(t)’ y R = KQ(t) para utilizar el flip-flop SR modificado para 4 combinaciones de entradas.
La siguiente tabla muestra la tabla de estados del flip-flop JK.
| J | K | Q(t + 1) |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q(t)’ |
Aquí, Q(t) & Q(t + 1) son el estado actual & el siguiente estado respectivamente. Así, el flip-flop JK puede ser utilizado para una de estas cuatro funciones como Hold, Reset, Set & Complemento de estado presente basado en las condiciones de entrada, cuando se aplica la transición positiva de la señal de reloj. La siguiente tabla muestra la tabla de características del flip-flop JK.
| Entradas presentes | Estado presente | Estado siguiente | |
|---|---|---|---|
| J | K | Q(t) | Q(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Al utilizar tres variables K-Map, podemos obtener la expresión simplificada para el próximo estado, Q(t + 1). Tres variables K-Map para el próximo estado, Q(t + 1) se muestra en la siguiente figura.
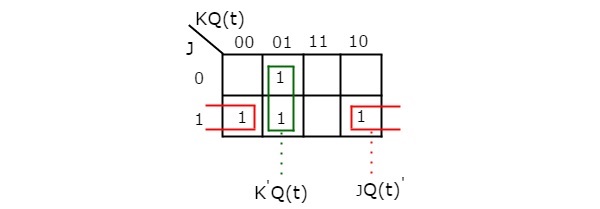
Las agrupaciones máximas posibles de adyacentes ya se muestran en la figura. Por tanto, la expresión simplificada para el siguiente estado Q(t+1) es
$$Q\left ( t+1 \right )=J{Q\left ( t \right )}’+{K}’Q\left ( t \right )$$
T Flip-Flop
T flip-flop es la versión simplificada de JK flip-flop. Se obtiene conectando la misma entrada ‘T’ a ambas entradas del flip-flop JK. Funciona sólo con transiciones de reloj positivas o negativas. El diagrama del circuito del flip-flop T se muestra en la siguiente figura.
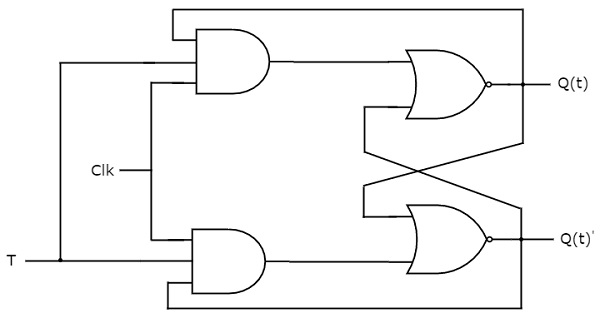
Este circuito tiene una sola entrada T y dos salidas Q(t) & Q(t)’. El funcionamiento del flip-flop T es el mismo que el del flip-flop JK. Aquí, consideramos las entradas del flip-flop JK como J = T y K = T para utilizar el flip-flop JK modificado para 2 combinaciones de entradas. Por lo tanto, eliminamos las otras dos combinaciones de J & K, para las cuales esos dos valores son complementarios entre sí en el flip-flop T.
La siguiente tabla muestra la tabla de estados del flip-flop T.
| D | Q(t + 1) |
|---|---|
| 0 | Q(t) |
| 1 | Q(t)’ |
Aquí, Q(t) & Q(t + 1) son el estado actual & siguiente estado, respectivamente. Por lo tanto, el flip-flop T puede ser utilizado para una de estas dos funciones como Hold, & Complemento del estado presente basado en las condiciones de entrada, cuando se aplica la transición positiva de la señal de reloj. La siguiente tabla muestra la tabla de características del flip-flop T.
| Entradas | Estado actual | Estado siguiente |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
A partir de la tabla característica anterior, podemos escribir directamente la siguiente ecuación de estado como
$$Q\left ( t+1 \right )={T}’Q\left ( t \right )+TQ{\left ( t \right )}’$$
$$$Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$
La salida de T flip-flop siempre conmuta por cada transición positiva de la señal de reloj, cuando la entrada T permanece en lógica alta (1). Por lo tanto, el flip-flop T se puede utilizar en contadores.
En este capítulo, hemos implementado varios flip-flops proporcionando el acoplamiento cruzado entre las puertas NOR. Del mismo modo, puede implementar estos flip-flops mediante el uso de puertas NAND.