Al principio, suele ser necesario hacerse una idea del diagrama pV del ciclo. Para ello trazaremos las curvas de los procesos isocóricos y adiabáticos. La gráfica aproximada del ciclo Otto se muestra en la siguiente figura.

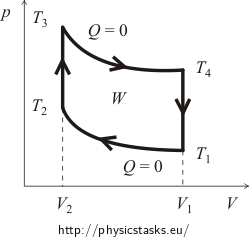
La eficiencia η del ciclo se define como

donde W es el trabajo realizado por el gas durante un ciclo menos el trabajo realizado por las fuerzas externas (¡en el diagrama está representado por la superficie del área definida por las líneas del ciclo!) y Qsup es el calor suministrado al sistema durante el ciclo.

El trabajo W se puede calcular utilizando la relación entre la presión y el volumen durante una expansión y compresión adiabática (el trabajo realizado durante un proceso isocórico es, por supuesto, cero). En esta tarea, sin embargo, será mejor utilizar el hecho de que el cambio total de la energía interna por ciclo debe ser igual a cero (volvemos al mismo estado que al principio, por lo que la temperatura y, por tanto, la energía interna siguen siendo las mismas). Según la primera ley de la termodinámica, el trabajo realizado por el gas puede expresarse como la diferencia entre el calor Qsup suministrado y el calor Qrel liberado. La fórmula de la eficiencia del ciclo es, por lo tanto, de la forma de

\N- 8942>Primero, calcularemos el calor suministrado Qsup. Está claro que durante el proceso adiabático no hay intercambio de calor y durante el enfriamiento isocórico se libera el calor. Esto significa que el calor será suministrado sólo durante el calentamiento isocórico desde la temperatura T2 hasta la temperatura T3. La cantidad de este calor puede expresarse en las variables de la cantidad de sustancia n del gas y de su capacidad calorífica molar CV de la siguiente manera: \N –

Expresaremos la cantidad de calor liberado Qrel de forma muy parecida. Ya sabemos que el calor se libera sólo durante el enfriamiento isocórico desde la temperatura T4 hasta la temperatura inicial T1. Es cierto que:

\

Ahora sustituimos estas fórmulas en la fórmula de la eficiencia del ciclo e inmediatamente obtenemos:

\

Ahora tendremos que expresar las diferencias de temperatura utilizando la relación de compresión dada

\

y la relación de Poisson κ.

Para ello, utilizaremos la ecuación para un gas ideal que sufre un proceso adiabático (la ley de Poisson) pVκ = C = konst., donde C es una constante. Ahora evaluamos la presión a partir de la ecuación de estado de un gas ideal

que sustituimos en la ley de Poisson. Ahora trasladamos las constantes (C y K) a un lado

\8942>Ahora aplicamos esta ley de Poisson para ambos procesos adiabáticos. Para la expansión adiabática obtenemos la relación \

Y para la compresión adiabática obtenemos

\

Ahora restamos la segunda ecuación de la primera y factorizamos V1κ – 1 por un lado y V2κ – 1 por el otro. Obtenemos:

\\Nde la ecuación

Vemos que realmente hemos conseguido expresar las diferencias de temperatura utilizando los valores dados.