Christian Bohr a koncept kooperativní vazbyEdit

V roce 1904 Christian Bohr studoval vazbu hemoglobinu na kyslík za různých podmínek. Při vykreslení grafu nasycení hemoglobinu kyslíkem v závislosti na parciálním tlaku kyslíku získal sigmoidální (neboli “esovitou”) křivku. Z toho vyplývá, že čím více kyslíku je na hemoglobin vázáno, tím snadněji se na něj váže další kyslík – až do nasycení všech vazebných míst. Bohr si navíc všiml, že zvyšující se tlak CO2 posouvá tuto křivku doprava – tj. vyšší koncentrace CO2 ztěžují vazbu kyslíku na hemoglobin. Tento druhý jev je spolu s pozorováním, že afinita hemoglobinu ke kyslíku se zvyšuje s rostoucím pH, známý jako Bohrův efekt.

Původní obrázek od Christiana Bohra, znázorňující sigmoidální nárůst oxyhemoglobinu v závislosti na parciálním tlaku kyslíku.

Říká se, že molekula receptoru vykazuje kooperativní vazbu, jestliže její vazba na ligand nelineárně škáluje s koncentrací ligandu. Kooperativita může být pozitivní (pokud vazba molekuly ligandu zvyšuje zdánlivou afinitu receptoru, a tím zvyšuje pravděpodobnost vazby další molekuly ligandu) nebo negativní (pokud vazba molekuly ligandu afinitu snižuje, a tím snižuje pravděpodobnost vazby dalších molekul ligandu). “Frakční obsazení” Y¯ {\displaystyle {\bar {Y}}}

receptoru s daným ligandem je definována jako podíl množství vazebných míst vázaných na ligand a celkového množství vazebných míst pro ligand: Y ¯ = + = {\displaystyle {\bar {Y}}={\frac {}{+}}={\frac {}{}}}

Pokud Y¯ = 0 {\displaystyle {\bar {Y}}=0}

, pak je protein zcela nevázaný, a pokud Y¯ = 1 {\displaystyle {\bar {Y}}=1}

, je zcela nasycen. Pokud je graf Y¯ {\displaystyle {\bar {Y}}} nasycený.

v rovnovážném stavu jako funkce koncentrace ligandu má sigmoidální tvar, jak to pozoroval Bohr u hemoglobinu, svědčí to o pozitivní kooperativitě. Pokud tomu tak není, nelze pouze na základě tohoto grafu učinit žádné prohlášení o kooperativitě.

Koncept kooperativní vazby se vztahuje pouze na molekuly nebo komplexy s více než jedním vazebným místem pro ligand. Pokud existuje více vazebných míst pro ligand, ale vazba ligandu na některé z nich neovlivňuje ostatní, říká se, že receptor není kooperativní. Kooperativita může být homotropní, pokud ligand ovlivňuje vazbu ligandů stejného druhu, nebo heterotropní, pokud ovlivňuje vazbu jiných druhů ligandů. V případě hemoglobinu Bohr pozoroval homotropní pozitivní kooperativitu (vazba kyslíku usnadňuje vazbu dalšího kyslíku) a heterotropní negativní kooperativitu (vazba CO2 snižuje schopnost hemoglobinu vázat kyslík.)

V průběhu 20. století byly vyvinuty různé rámce pro popis vazby ligandu na protein s více než jedním vazebným místem a kooperativních efektů pozorovaných v této souvislosti.

Hillova rovniceEdit

První popis kooperativní vazby na protein s více vazebnými místy vypracoval A. V. Hill. Na základě pozorování vazby kyslíku na hemoglobin a myšlenky, že kooperativita vzniká agregací molekul hemoglobinu, z nichž každá váže jednu molekulu kyslíku, navrhl Hill fenomenologickou rovnici, která byla od té doby pojmenována po něm:

Hillův graf červeně znázorňující sklon křivky, který je Hillovým koeficientem, a průsečík s osou x udávající zdánlivou disociační konstantu. Zelená čára znázorňuje nespolupracující křivku.

Y¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\displaystyle {\bar {Y}}={\frac {K\cdot {}^{n}}{1+K\cdot {}^{n}}}={\frac {^{n}}{K^{*}+^{n}}}={\frac {^{n}}{K_{d}^{n}+^{n}}}}

kde n {\displaystyle n}

je “Hillův koeficient”, {\displaystyle }

označuje koncentraci ligandu, K {\displaystyle K}

označuje zdánlivou asociační konstantu (použitou v původní podobě rovnice), K ∗ {\displaystyle K^{*}}

je empirická disociační konstanta a K d {\displaystyle K_{d}} je empirická disociační konstanta.

je mikroskopická disociační konstanta (používá se v moderních formách rovnice a je ekvivalentní E C 50 {\displaystyle \mathrm {EC} _{50}}

). Je-li n < 1 {\displaystyle n<1}.

, systém vykazuje zápornou kooperativitu, zatímco kooperativita je kladná, pokud n > 1 {\displaystyle n>1}.

. Celkový počet vazebných míst pro ligandy je horní hranicí pro n {\displaystyle n}.

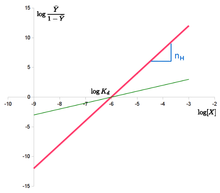
. Hillovu rovnici lze linearizovat jako: log Y¯ 1 – Y¯ = n ⋅ log – n ⋅ log K d {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}=n\cdot {}\log-n\cdot {}\log K_{d}}.

“Hillův graf” se získá vynesením log Y¯ 1 – Y¯ {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}}

versus log {\displaystyle \log}

. V případě Hillovy rovnice se jedná o přímku se sklonem n H {\displaystyle n_{H}}.

a intercepcí log ( K d ) {\displaystyle \log(K_{d})}

. To znamená, že kooperativita se předpokládá jako pevná, tj. nemění se s nasycením. Znamená to také, že vazebná místa vykazují vždy stejnou afinitu a kooperativita nevyplývá z afinity rostoucí s koncentrací ligandu.

Adairova rovniceEdit

G. S. Adair zjistil, že Hillův graf pro hemoglobin není přímka, a vyslovil hypotézu, že vazebná afinita není pevný člen, ale závisí na nasycení ligandem. Poté, co prokázal, že hemoglobin obsahuje čtyři hemy (a tedy vazebná místa pro kyslík), pracoval s předpokladem, že plně nasycený hemoglobin se tvoří postupně, s přechodnými formami s jednou, dvěma nebo třemi vázanými molekulami kyslíku. Vznik každého mezistupně z nenavázaného hemoglobinu lze popsat pomocí zdánlivé makroskopické asociační konstanty K i {\displaystyle K_{i}}.

. Výslednou frakční obsazenost lze vyjádřit jako: Y¯ = 1 4 ⋅ K I + 2 K I I 2 + 3 K I I I 3 + 4 K I V 4 1 + K I + K I I 2 + K I I I 3 + K I V 4 {\displaystyle {\bar {Y}}={\frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, pro libovolný protein s n vazebnými místy pro ligandy:

Y¯ = 1 n K I + 2 K I I 2 + … + n K n n 1 + K I + K I I 2 + … + K n n {\displaystyle {\bar {Y}}={\frac {1}{n}}{\frac {K_{I}+2K_{II}^{2}+\ldots +nK_{n}^{n}}{1+K_{I}+K_{II}^{2}+\ldots +K_{n}^{n}}}}

kde n označuje počet vazebných míst a každé K i {\displaystyle K_{i}}

je kombinovaná asociační konstanta, popisující vazbu i molekul ligandu. kombinací Adairova zpracování s Hillovým grafem se dospěje k moderní experimentální definici kooperativity (Hill, 1985, Abeliovich, 2005). Výsledný Hillův koeficient, nebo správněji sklon Hillova grafu vypočtený z Adairovy rovnice, lze ukázat jako poměr mezi rozptylem vazebného čísla a rozptylem vazebného čísla v ekvivalentním systému neinteragujících vazebných míst. Hillův koeficient tedy definuje kooperativitu jako statistickou závislost jednoho vazebného místa na stavu jiného místa (jiných míst).

Klotzova rovniceEdit

Pracoval na proteinech vázajících vápník, Irving Klotz dekonvertoval Adairovy asociační konstanty tím, že uvažoval postupnou tvorbu mezistupňů, a pokusil se vyjádřit kooperativní vazbu v termínech elementárních procesů řízených zákonem působení hmoty. V jeho rámci je K 1 {\displaystyle K_{1}}

je asociační konstanta řídící vazbu první molekuly ligandu, K 2 {\displaystyle K_{2}}.

je asociační konstanta řídící vazbu druhé molekuly ligandu (poté, co je první molekula již navázána) atd. Pro Y¯ {\displaystyle {\bar {Y}}}

, to dává: Y¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … K n ). K n ) n {\displaystyle {\bar {Y}}={\frac {1}{n}}{\frac {K_{1}+2K_{1}K_{2}^{2}+\ldots +n\left(K_{1}K_{2}\ldots) K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Je třeba poznamenat, že konstanty K 1 {\displaystyle K_{1}}

, K 2 {\displaystyle K_{2}}.

apod. se nevztahují k jednotlivým vazebným místům. Popisují spíše, kolik vazebných míst je obsazeno, než která. Tato forma má tu výhodu, že při posuzování asociačních konstant lze snadno rozpoznat kooperativitu. Pokud jsou všechna vazebná místa ligandu identická s mikroskopickou asociační konstantou K {\displaystyle K}

, lze očekávat, že K 1 = n K , K 2 = n – 1 2 K , …. K n = 1 n K {\displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}K,\ldots K_{n}={\frac {1}{n}}K}

(tedy K i = n – i + 1 i K {\displaystyle K_{i}={\frac {n-i+1}{i}}K}

) při absenci kooperativity. Kladnou kooperativitu máme, jestliže K i {\displaystyle K_{i}}

leží nad těmito očekávanými hodnotami pro i > 1 {\displaystyle i>1}.

.

Klotzova rovnice (která se někdy také nazývá Adair-Klotzova rovnice) se v experimentální literatuře stále často používá k popisu měření vazby ligandů ve smyslu postupných zdánlivých vazebných konstant.

Paulingova rovniceEdit

V polovině 20. století vzrostl zájem o modely, které by nejen fenomenologicky popisovaly vazebné křivky, ale nabízely i základní biochemický mechanismus. Linus Pauling reinterpretoval rovnici poskytnutou Adairem a předpokládal, že jeho konstanty jsou kombinací vazebné konstanty pro ligand ( K {\displaystyle K}

v rovnici níže) a energie pocházející z interakce mezi podjednotkami kooperujícího proteinu ( α {\displaystyle \alpha }

níže). Pauling ve skutečnosti odvodil několik rovnic v závislosti na stupni interakce mezi podjednotkami. Na základě chybných předpokladů o lokalizaci hemů zvolil pro popis vazby kyslíku hemoglobinem špatnou z nich za předpokladu, že podjednotky byly uspořádány do čtverce. Následující rovnice uvádí rovnici pro tetraedrickou strukturu, která by byla v případě hemoglobinu přesnější: Y¯ = K + 3 α K 2 2 + 3 α 3 K 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 + 4 α 3 K 3 3 + α 6 K 4 4 {\displaystyle {\bar {Y}}={\frac {K+3\alfa {}K^{2}^{2}+3\alfa {}^{3}K^{3}^{3}+\alfa {}^{6}K^{4}^{4}}{1+4K+6\alfa {}K^{2}^{2}+4\alfa {}^{3}K^{3}^{3}+\alfa {}^{6}K^{4}^{4}}}}

Model KNFEdit

Založeno na výsledcích, které ukazují, že struktura kooperativních proteinů se mění při vazbě na jejich ligand, Daniel Koshland a jeho kolegové zpřesnili biochemické vysvětlení mechanismu popsaného Paulingem. Model Koshland-Némethy-Filmer (KNF) předpokládá, že každá podjednotka může existovat v jedné ze dvou konformací: aktivní nebo neaktivní. Vazba ligandu na jednu podjednotku vyvolá okamžitou konformační změnu této podjednotky z neaktivní do aktivní konformace, což je mechanismus popsaný jako “indukované přizpůsobení”. Kooperativita by podle modelu KNF vyplývala z interakcí mezi podjednotkami, jejichž síla se mění v závislosti na relativní konformaci zúčastněných podjednotek. Pro tetraedrickou strukturu (uvažovali také lineární a čtvercové struktury) navrhli následující vzorec:

Y¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B ( K X K t ) 2 + 3 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {\displaystyle {\bar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Kde K X {\displaystyle K_{X}}

je konstanta asociace pro X, K t {\displaystyle K_{t}}

je poměr stavů B a A v nepřítomnosti ligandu (“přechod”), K A B {\displaystyle K_{AB}}

a K B B {\displaystyle K_{BB}}

jsou relativní stability dvojic sousedních podjednotek vzhledem k dvojici, kde jsou obě podjednotky ve stavu A (Všimněte si, že v článku KNF se ve skutečnosti uvádí N s {\displaystyle N_{s}}

, počet obsazených míst, který je zde 4krát Y¯ {\displaystyle {\bar {Y}}}.

).

Model MWCUpravit

Monod-Wyman-Changeux modelové reakční schéma proteinu složeného ze dvou protomerů. Protomer může existovat ve dvou stavech, z nichž každý má jinou afinitu k ligandu. L je poměr stavů v nepřítomnosti ligandu, c je poměr afinit.

Energetické schéma Monod-Wyman-Changeuxova modelu proteinu tvořeného dvěma protomery. Větší afinita ligandu ke stavu R znamená, že tento stav je vazbou přednostně stabilizován.

Monod-Wyman-Changeuxův (MWC) model pro sladěné alosterické přechody šel o krok dále a zkoumal kooperativitu na základě termodynamiky a trojrozměrných konformací. Původně byl formulován pro oligomerní proteiny se symetricky uspořádanými identickými podjednotkami, z nichž každá má jedno vazebné místo pro ligand. Podle tohoto rámce koexistují dva (nebo více) vzájemně konvertibilní konformační stavy alosterického proteinu v tepelné rovnováze. Tyto stavy – často označované jako napjatý (T) a uvolněný (R) – se liší afinitou k molekule ligandu. Poměr mezi oběma stavy je regulován vazbou molekul ligandu, který stabilizuje stav s vyšší afinitou. Důležité je, že všechny podjednotky molekuly mění stavy současně, což je jev známý jako “sladěný přechod”.

Alosterická izomerizační konstanta L popisuje rovnováhu mezi oběma stavy, když není vázána žádná molekula ligandu: L = {\displaystyle L={\frac {\left}{\left}}}

. Pokud je L velmi velké, většina proteinu existuje ve stavu T bez přítomnosti ligandu. Pokud je L malé (blízké jedné), je stav R téměř stejně zaplněn jako stav T. Poměr disociačních konstant pro ligand ze stavů T a R je popsán konstantou c: c = K d R K d T {\displaystyle c={\frac {K_{d}^{R}}{K_{d}^{T}}}}

. Je-li c = 1 {\displaystyle c=1}

, mají stavy R i T stejnou afinitu k ligandu a ligand neovlivňuje izomerizaci. Hodnota c také udává, jak moc se změní rovnováha mezi stavy T a R po navázání ligandu: čím menší c, tím více se rovnováha po jedné vazbě posune směrem ke stavu R. S α = K d R {\displaystyle \alpha ={\frac {}{K_{d}^{R}}}}

, je frakční obsazení popsáno jako: Y¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {Y}}={\frac {\alfa (1+\alfa )^{n-1}+Lc\alfa (1+c\alfa )^{n-1}}{(1+\alfa )^{n}+L(1+c\alfa )^{n}}}}

Sigmoidní Hillův graf alosterických proteinů pak lze analyzovat jako postupný přechod ze stavu T (nízká afinita) do stavu R (vysoká afinita) s rostoucí saturací. Sklon Hillova grafu rovněž závisí na nasycení, s maximální hodnotou v inflexním bodě. Průsečíky mezi oběma asymptotami a osou y umožňují určit afinitu obou stavů k ligandu.

Hillův graf vazebné funkce MWC červeně, čistého stavu T a R zeleně. S posunem konformace z T do R se mění i vazebná funkce. Průsečíky s osou x poskytují zdánlivou disociační konstantu i mikroskopické disociační konstanty stavů R a T.

U proteinů je konformační změna často spojena s aktivitou nebo aktivitou vůči specifickým cílům. Taková aktivita je často tím, co je fyziologicky relevantní nebo co se experimentálně měří. Stupeň konformační změny je popsán stavovou funkcí R¯ {\displaystyle {\bar {R}}}.

, která označuje podíl proteinu přítomného ve stavu R {\displaystyle R}

state. Jak znázorňuje energetický diagram, R¯ {\displaystyle {\bar {R}}}

roste s tím, jak se váže více molekul ligandu. Výraz pro R¯ {\displaystyle {\bar {R}}

je: R¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {R}}={\frac {(1+\alfa )^{n}}{(1+\alfa )^{n}+L(1+c\alfa )^{n}}}}

Klíčovým aspektem modelu MWC je, že křivky pro Y¯ {\displaystyle {\bar {Y}}}

a R¯ {\displaystyle {\bar {R}}}

se neshodují, tj. frakční nasycení není přímým ukazatelem konformačního stavu (a tedy ani aktivity). Rozsah kooperativity vazby a kooperativity aktivace se navíc může velmi lišit: extrémní případ poskytuje motor bičíků bakterií s Hillovým koeficientem 1,7 pro vazbu a 10,3 pro aktivaci. Nadlinearita reakce se někdy nazývá ultrasenzitivita.

Váže-li se alosterický protein na cíl, který má také vyšší afinitu ke stavu R, pak vazba na cíl dále stabilizuje stav R, a tedy zvyšuje afinitu k ligandu. Pokud se naopak cíl přednostně váže na stav T, pak bude mít vazba na cíl negativní vliv na afinitu ligandu. Takové cíle se nazývají alosterické modulátory.

Od svého vzniku byl rámec MWC rozšířen a zobecněn. Byly navrženy varianty, které například zohledňují proteiny s více než dvěma stavy, proteiny, které se vážou na několik typů ligandů nebo několik typů alosterických modulátorů, a proteiny s neidentickými podjednotkami nebo vazebnými místy pro ligandy.