En La guerra de los mundos, unos gigantescos robots alienígenas emergen del suelo y comienzan a vaporizar a un gran número de actores. Hay muchas cosas que me gustan en esas escenas, pero hay tres cosas que no pude soportar.
Como esas tres patas con las que caminaban. No su frágil apariencia enjuta, sino sus tres patas reales.
Por favor, primero Tom Cruise, primero Tom Cruise, por favor…
Debería haber más piernas. Unas seis, en concreto.
“Mira”, podrías responder, “es una nave alienígena, y quién sabe qué tipo de principios han descubierto”.
Por supuesto, eso es posible. Pero otra forma de verlo es que los terrícolas tenemos una gran variedad de planes corporales y de extremidades, y sin embargo no encontramos el diseño de tres extremidades en ninguna parte. Tal vez ese sea un buen argumento para decir que los extraterrestres no construirían una nave con tres patas.
¿Qué hacemos los terrícolas para el diseño de las extremidades?
Tendemos a seguir una ley, una que puede atravesar todos los filos animales, una ley que publiqué por primera vez en el Journal of Theoretical Biology en 2001 , y que elaboré en mi primer libro The Brain from 25,000 Feet .
Esta “ley de las extremidades” relaciona el número de extremidades de un animal con la longitud de esas extremidades (en relación con el tamaño del cuerpo).
Cuando las extremidades de un animal son muy largas en relación con el tamaño de su cuerpo, argumenté que la solución óptima para alcanzarlas (que utiliza la menor cantidad de “cable” o material de las extremidades) es tener unas seis extremidades. (Esto se aplica a los animales con extremidades dirigidas aproximadamente de forma radial alrededor de un perímetro. Para los animales cuyas direcciones de los miembros se extienden uniformemente sobre una superficie esférica, el número esperado de miembros en este caso sería de unos 12.)
A medida que los miembros del animal se acortan en relación con el tamaño del cuerpo, el número esperado de miembros aumenta, con un número tremendo de miembros cuando los miembros son muy cortos. (Por cierto, una serpiente es consistente con un número infinito de extremidades infinitamente cortas – es decir, sin extremidades.)
Más generalmente, la ley predice que el número de extremidades de un animal es inversamente proporcional a la longitud relativa de las extremidades. Y, más concretamente, la ley predice una constante de proporcionalidad particular, de modo que “seis” es la solución en el caso de extremidades realmente largas.
Siendo L la longitud de las extremidades y R el radio del cuerpo del animal, entonces k = L / (L + R) es la longitud relativa de las extremidades, o “ratio de extremidades”.
Se espera que el número de extremidades, N, varíe aproximadamente como
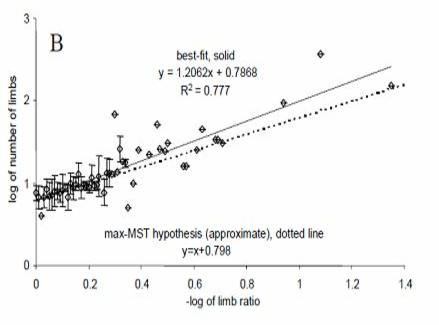
La figura siguiente (de mi primer libro) muestra cómo el número de miembros se relaciona de hecho con la proporción de miembros, para 190 especies a través de siete filos animales (Annelida, Arthropoda, Cnidaria, Echinodermata, Mollusca, Vertebrata y Tardigrada).
La tendencia predicha se muestra con la línea sólida, consistente con la ecuación N ≈ 6,28k-1 que vimos justo arriba.
La tendencia real se muestra con la línea punteada, lo que lleva a una ecuación empírica de N ≈6,24k-1,17 … o sea, muy cercana a la predicción.
Para tener una mejor impresión de la Ley de las Extremidades que parecen seguir los terrícolas, echa un vistazo a este pequeño programa visual dinámico de Eric Bolz, que permite variar la longitud de las extremidades y ver cómo varía el número de éstas: http://www.changizi.com/limb.html El eje vertical derecho le permite modular la relación de las extremidades y ver cómo cambia el número de éstas. El eje inferior te permite hacer criaturas más largas o más cortas. El eje vertical izquierdo sólo te permite cambiar el tamaño de la criatura en la página.
Las naves alienígenas de La Guerra de los Mundos deberían tener -dada la gran longitud de sus extremidades y asumiendo que deben ser tratadas como si apuntaran aproximadamente a un perímetro- unas seis extremidades. No tres.
Por eso parecen tan tontas. Están fuera del punto dulce en el espacio de diseño para las extremidades.
En mi próximo artículo, discutiré cómo esta idea de las extremidades nos dice por qué tenemos 10 dedos, y tal vez, por lo tanto, por qué tenemos un sistema numérico de base-10.