Grafer i Python

Grafteoriens oprindelse

Hvor vi begynder med de egentlige implementeringer af grafer i Python, og før vi begynder med introduktionen af Python-moduler, der beskæftiger sig med grafer, vil vi hellige os grafteoriens oprindelse.
Oprindelsen fører os tilbage i tiden til Künigsberg i det 18. århundrede. Königsberg var dengang en by i Preussen. Floden Pregel flød gennem byen og skabte to øer. Byen og øerne var forbundet af syv broer som vist. Byens indbyggere blev bevæget af spørgsmålet, om det var muligt at gå en tur gennem byen ved at besøge hvert område af byen og kun krydse hver bro én gang? Hver bro skal være krydset helt og holdent, dvs. det er ikke tilladt at gå halvvejs på en bro og så vende om og senere krydse den anden halvdel fra den anden side. Gåturen behøver ikke at starte og slutte samme sted. Leonhard Euler løste problemet i 1735 ved at bevise, at det ikke er muligt. Han fandt ud af, at valget af en rute inden for hvert landområde er irrelevant, og at det eneste, der betyder noget, er rækkefølgen (eller rækkefølgen), i hvilken broerne krydses. Han havde formuleret en abstraktion af problemet, idet han eliminerede unødvendige fakta og fokuserede på landområderne og de broer, der forbinder dem. På denne måde skabte han grundlaget for grafteori. Hvis vi ser et “landområde” som et toppunkt og hver bro som en kant, har vi “reduceret” problemet til en graf.

Introduktion til grafteori ved hjælp af Python

Hvor vi begynder vores behandling af mulige Python-repræsentationer af grafer, vil vi præsentere nogle generelle definitioner af grafer og deres komponenter.
En “graf “1 i matematik og datalogi består af “knuder”, også kaldet “vertices”.
Knuder kan være forbundet med hinanden eller ej. I vores illustration, – som er en billedlig fremstilling af en graf, – er knuden “a” forbundet med knuden “c”, men “a” er ikke forbundet med “b”. En forbindelseslinje mellem to knuder kaldes en kant. Hvis kanterne mellem knuderne er udirigerede, kaldes grafen for en udirigeret graf. Hvis en kant er rettet fra et toppunkt (knudepunkt) til et andet, kaldes en graf for en rettet graf. En rettet kant kaldes en bue.
Og selv om grafer kan se meget teoretiske ud, kan mange praktiske problemer repræsenteres ved hjælp af grafer. De bruges ofte til at modellere problemer eller situationer inden for fysik, biologi, psykologi og frem for alt inden for datalogi. Inden for datalogi bruges grafer til at repræsentere kommunikationsnetværk, dataorganisation, beregningsenheder, beregningsflowet,

I sidstnævnte tilfælde bruges graferne til at repræsentere dataorganisationen, som f.eks. filsystemet i et styresystem, eller kommunikationsnetværk. Linkstrukturen på websteder kan også ses som en graf, dvs. en rettet graf, fordi et link er en rettet kant eller en bue.
Python har ingen indbygget datatype eller klasse for grafer, men det er let at implementere dem i Python. Der er én datatype, der er ideel til at repræsentere grafer i Python, nemlig ordbøger. Grafen i vores illustration kan implementeres på følgende måde:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Nøglerne i ordbogen ovenfor er knuderne i vores graf. De tilsvarende værdier er lister med knuderne, som er forbundet med en kant. Der findes ingen enklere og mere elegant måde at repræsentere en graf på.
En kant kan ses som en 2-tupel med knuder som elementer, dvs. (“a”, “b”)
Funktion til generering af listen over alle kanter:Denne kode genererer følgende output, hvis den kombineres med den tidligere definerede grafordbog:

 $ python3 graph_simple.py 

Som vi kan se, er der ingen kant, der indeholder knuden “f”. “f” er en isoleret knude i vores graf.
Følgende Python-funktion beregner de isolerede knuder i en given graf:Hvis vi kalder denne funktion med vores graf, vil en liste, der indeholder “f”, blive returneret:

Grafer som en Python-klasse

Hvor vi fortsætter med at skrive funktioner til grafer, skal vi for første gang forsøge os med en implementering af en Python-klasse til grafer. Hvis du kigger på følgende listing af vores klasse, kan du se i __init__-metoden, at vi bruger en ordbog “self.__graph_dict” til at lagre vertices og deres tilsvarende tilstødende vertices.
Hvis du starter dette modul standalone, vil du få følgende resultat:

Stier i grafer

Vi ønsker nu at finde den korteste sti fra et knudepunkt til et andet knudepunkt. Inden vi kommer til Python-koden til dette problem, er vi nødt til at præsentere nogle formelle definitioner.
Nærliggende hjørner:
To hjørner er nærliggende, når de begge er tilstødende til en fælles kant.
Sti i en udirigeret graf:
En sti i en udirigeret graf er en sekvens af hjørner P = ( v1, v2, …., vn ) ∈ V x V x … x V således, at vi støder op til v{i+1} for 1 ≤ i < n. En sådan sti P kaldes en sti af længde n fra v1 til vn.
En simpel sti:
En sti uden gentagne toppunkter kaldes en simpel sti.
Eksempel:
(a, c, e) er en simpel sti i vores graf, ligesom (a,c,e,b). (a,c,e,b,c,d) er en sti, men ikke en simpel sti, fordi knuden c optræder to gange.
Følgende metode finder en sti fra et startvertex til et slutvertex: Hvis vi gemmer vores grafklasse inklusive find_path-metoden som “graphs.py”, kan vi kontrollere arbejdsgangen for vores find_path-funktion: Resultatet af det foregående program ser således ud:

Metoden find_all_paths finder alle stier mellem et startvertex og et slutvertex:Vi har ændret vores eksempelgraf en smule ved at tilføje kanter fra “a” til “f” og fra “f” til “d” for at afprøve den tidligere definerede metode:Resultatet ser således ud: Vi har ændret vores eksempelgraf en smule ved at tilføje kanter fra “a” til “f” og fra “f” til “d” for at teste den tidligere definerede metode:Resultatet ser således ud:

Grad

Graden af et toppunkt v i en graf er antallet af kanter, der forbinder det, idet løkker tælles to gange. Graden af et toppunkt v betegnes deg(v). Den maksimale grad af en graf G, angivet med Δ(G), og den minimale grad af en graf, angivet med δ(G), er den maksimale og minimale grad af dens toppene.
I grafen til højre er den maksimale grad 5 ved toppunktet c og den minimale grad 0, dvs. det isolerede toppunkt f.
Hvis alle grader i en graf er ens, er grafen en regulær graf.
I en regulær graf er alle grader ens, og derfor kan vi tale om gradens grad.
Gradsummeformlen (Handshaking lemma):
∑v &in; Vdeg(v) = 2 |E|
Det betyder, at summen af grader for alle toppene er lig med antallet af kanter ganget med 2. Vi kan konkludere, at antallet af toppene med ulige grader må være lige. Denne påstand er kendt som “handshaking lemmaet”. Navnet “handshaking lemma” stammer fra et populært matematisk problem: I en hvilken som helst gruppe af mennesker er antallet af personer, der har givet hånd til et ulige antal andre personer fra gruppen, lige.
Følgende metode beregner graden af et toppunkt:
Følgende metode beregner en liste med de isolerede toppunkter i en graf:Metoderne delta og Delta kan anvendes til at beregne henholdsvis den mindste og den største grad af et toppunkt:

Gradssekvens

Gradssekvensen for en udirigeret graf er defineret som sekvensen af dens toppegrader i en ikke-vækstende rækkefølge.
Følgende metode returnerer en tupel med gradssekvensen for eksempelgrafen:
Gradsekvensen for vores eksempelgraf er følgende sekvens af hele tal: (5,2,1,1,1,0).
Isomorfe grafer har den samme gradsrækkefølge. To grafer med den samme gradsrækkefølge er dog ikke nødvendigvis isomorfe.
Der er spørgsmålet, om en given gradsrækkefølge kan realiseres af en simpel graf. Erdös-Gallai-sætningen fastslår, at en ikke-vækstende sekvens af n tal di (fori = 1, …, n) er en simpel gradssekvens af en simpel graf, hvis og kun hvis summen af sekvensen er lige, og følgende betingelse er opfyldt:

Implementering af Erdös-Gallai-sætningen

Vores grafklasse – se længere nede for en komplet liste – indeholder en metode “erdoes_gallai”, der afgør, om en sekvens opfylder Erdös-Gallai-sætningen. Først kontrollerer vi, om summen af elementerne i sekvensen er ulige. Hvis det er tilfældet, returnerer funktionen False, fordi Erdös-Gallai-sætningen ikke længere kan opfyldes. Herefter kontrollerer vi med den statiske metode is_degree_sequence, om den indtastede sekvens er en gradssekvens, dvs. at elementerne i sekvensen er ikke-vækstende. Dette er lidt overflødigt, da det er meningen, at input skal være en gradsrækkefølge, så du kan droppe denne kontrol af hensyn til effektiviteten. Nu kontrollerer vi i kroppen af den anden if-erklæring, om sætningens ulighed er opfyldt:

Version uden den overflødige gradfølge-test:

Graftæthed

Graftætheden er defineret som forholdet mellem antallet af kanter i en given graf og det samlede antal kanter, grafen kunne have. Med andre ord: Den måler, hvor tæt en given graf er på en komplet graf.
Den maksimale tæthed er 1, hvis en graf er komplet. Dette er klart, fordi det maksimale antal kanter i en graf afhænger af hjørnerne og kan beregnes som:
max. antal kanter = ½ * |V| * ( |V| – 1 ).
På den anden side er den minimale tæthed 0, hvis grafen ikke har nogen kanter, dvs. at det er en isoleret graf.
For udirigerede simple grafer er graftætheden defineret som: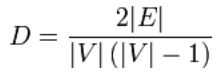

En tæt graf er en graf, hvor antallet af kanter er tæt på det maksimale antal kanter. En graf med kun få kanter kaldes en sparsom graf. Definitionen for disse to udtryk er ikke særlig skarp, dvs. der er ingen mindste øvre grænse (supremum) for en sparsom tæthed og ingen største nedre grænse (infimum) for at definere en tæt graf.
Den mest præcise matematiske notation anvender den store O-notation:
Sparse Graph:
Tæt graf:
En tæt graf er en graf G = (V, E), hvor |E| = Θ(|V|2).
“density” er en metode i vores klasse til at beregne tætheden af en graf:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Vi kan teste denne metode med følgende script. En komplet graf har en tæthed på 1, og en isoleret graf har en tæthed på 0, som vi kan se af resultaterne af det foregående testskript:

$ python test_density.py 0.4666666666671.00.0

Sammenhængende grafer

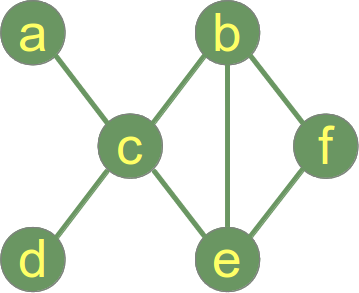En graf siges at være forbundet, hvis hvert par af toppunkter i grafen er forbundet. Eksempelgrafen til højre er en forbundet graf.
Det er muligt at bestemme med en simpel algoritme, om en graf er forbundet:

1. Vælg en vilkårlig knude x i grafen G som udgangspunkt
2. Bestem mængden A af alle de knuder, som kan nås fra x.
3. Hvis A er lig med mængden af knuder i G, er grafen forbundet; ellers er den frakoblet.

Vi implementerer en metode is_connected til at kontrollere, om en graf er en forbundet graf. Vi lægger ikke vægt på effektivitet, men på læsbarhed.
Hvis du tilføjer denne metode til vores grafklasse, kan vi teste den med følgende script. Under forudsætning af, at du gemmer grafklassen som graph2.py:
En forbundet komponent er en maksimalt forbundet undergraf af G. Hvert toppunkt tilhører præcis én forbundet komponent, hvilket også gælder for hver kant.

Afstand og diameter af en graf

Afstanden “dist” mellem to toppunkter i en graf er længden af den korteste vej mellem disse toppunkter. Ingen backtracks, omveje eller sløjfer er tilladt ved beregning af en afstand.

I vores eksempelgraf til højre er afstanden mellem toppunktet a og toppunktet f 3, dvs. dist(a,f) = 3, fordi den korteste vej går via toppunkterne c og e (eller alternativt c og b).
Ekcentriciteten af et toppunkt s i en graf g er den maksimale afstand til alle andre toppunkter i grafen:
e(s) = max( { dist(s,v) | v ∈ V })
(V er mængden af alle toppunkter i g)
Diameteren d i en graf er defineret som den maksimale excentricitet af et hvilket som helst toppunkt i grafen. Det betyder, at diameteren er længden af den korteste vej mellem de mest afsidesliggende knuder. For at bestemme diameteren af en graf skal man først finde den korteste vej mellem hvert par toppunkter. Den største længde af enhver af disse stier er grafernes diameter.
Vi kan direkte se i vores eksempelgraf, at diameteren er 3, fordi den mindste længde mellem a og f er 3, og der er ikke noget andet toppunktspar med en længere sti.
Den følgende metode implementerer en algoritme til beregning af diameteren. Vi kan beregne diameteren for vores eksempelgraf med følgende script, idet vi igen antager, at vores komplette grafklasse er gemt som graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Det vil udskrive værdien 3.

Den komplette Python-grafklasse

I følgende Python-kode finder du det komplette Python-klassemodul med alle de omtalte metoder:graph2.py

Træ / skov

Et træ er en udirigeret graf, som ikke indeholder nogen cyklusser. Det betyder, at to vilkårlige toppunkter i grafen er forbundet af præcis én simpel sti.
En skov er en disjoint union af træer. I modsætning til skove i naturen kan en skov i grafteori bestå af et enkelt træ!
En graf med ét toppunkt og ingen kant er et træ (og en skov).
Et eksempel på et træ: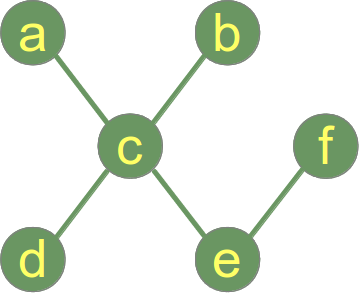

Mens det foregående eksempel viser en graf, som er et træ og en skov, viser det følgende billede en graf, som består af to træer, dvs.Dvs. grafen er en skov, men ikke et træ:

Oversigt over skove:

Med ét toppunkt:

Skovgrafer med to toppunkter:

Skovgrafer med to toppunkter:

Skovgrafer med tre toppunkter:

Spændetræ

Et spændetræ T af en sammenhængende, udirigeret graf G er en undergraf G’ af G, som er et træ, og G’ indeholder alle toppene og en delmængde af kanterne i G. G’ indeholder alle kanterne i G, hvis G er en trægraf. Uformelt set er et spændetræ i G et udvalg af kanter i G, der danner et træ, der spænder over alle toppene. Det vil sige, at hvert toppunkt ligger i træet, men at der ikke er nogen cyklusser (eller sløjfer) i træet.
Eksempel:
En fuldt sammenhængende graf: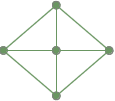

To spændene træer fra den foregående fuldt sammenhængende graf: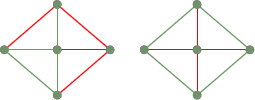

Hamiltonsk spil

En Hamiltonsk sti er en sti i en udirigeret eller dirigeret graf, der besøger hvert toppunkt præcis én gang. En Hamiltonian cyklus (eller kredsløb) er en Hamiltonian sti, der er en cyklus.
Note til dataloger: Generelt er det ikke muligt at afgøre, om der findes sådanne stier eller kredsløb i vilkårlige grafer, fordi Hamiltonian path-problemet har vist sig at være NP-komplet.
Det er opkaldt efter William Rowan Hamilton, der opfandt det såkaldte “icosian game” eller Hamiltons puslespil, som går ud på at finde et Hamiltonian cycle i dodekaederets kantgraf. Hamilton løste dette problem ved hjælp af icosian calculus, en algebraisk struktur baseret på rødder af enhed med mange ligheder med quaternionerne, som han også opfandt.

Komplet liste over Graph-klassen

Vi kan teste denne Graph-klasse med følgende program:Hvis vi starter dette program, får vi følgende output:
Fodnoter:
1 De grafer, der studeres i grafteori (og i dette kapitel i vores Python-tutorial), skal ikke forveksles med graferne for funktioner
2 En singleton er en mængde, der indeholder præcis ét element.
Kredittering:
Narayana Chikkam, nchikkam(at)gmail(dot)com, gjorde os opmærksom på en indeksfejl i metoden “erdoes_gallai”. Mange tak, Narayana!