I det foregående kapitel har vi talt om Latches. Disse er de grundlæggende byggesten i flip-flops. Vi kan implementere flip-flops på to metoder.
I den første metode kaskaderes to latches på en sådan måde, at den første latch aktiveres for hver positiv clockpuls og den anden latch aktiveres for hver negativ clockpuls. Så kombinationen af disse to latches bliver en flip-flop.
I den anden metode kan vi direkte implementere flip-flopet, som er flankefølsomt. I dette kapitel skal vi diskutere følgende flip-flops ved hjælp af anden metode.
- SR Flip-Flop
- D Flip-Flop
- JK Flip-Flop
- T Flip-Flop
SR Flip-Flop
SR flip-flop fungerer kun med positive clockovergange eller negative clockovergange. SR-latch fungerer derimod med aktiveringssignal. Kredsløbsdiagrammet for SR-flip-flop er vist i følgende figur.
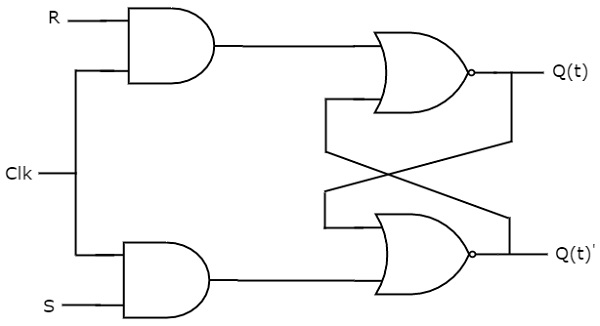
Dette kredsløb har to indgange S & R og to udgange Q(t) & Q(t)’. SR-flipflop fungerer på samme måde som SR Latch. Men denne flip-flop påvirker kun udgangene, når der anvendes positiv overgang af klokkesignalet i stedet for aktiv enable.
Den følgende tabel viser tilstandstabellen for SR-flip-flop.
| R | ||
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | – |
Her, Q(t) & Q(t + 1) er henholdsvis nuværende tilstand & næste tilstand. Så SR-flipflop kan anvendes til en af disse tre funktioner såsom Hold, Reset & Set baseret på indgangsbetingelserne, når der anvendes en positiv overgang af ur-signalet. Følgende tabel viser den karakteristiske tabel for SR-flipflop.
| På nuværende indgange | På nuværende tilstand | |||
|---|---|---|---|---|
| S | R | Q(t) | Q(t + 1) | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | x | |
| 1 | 1 | 1 | 1 | x |
Ved anvendelse af tre variable K-kort, kan vi få det forenklede udtryk for den næste tilstand, Q(t + 1). K-kortet med tre variabler for næste tilstand, Q(t + 1), er vist i følgende figur.
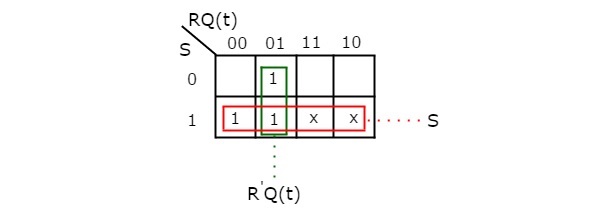
De maksimale mulige grupperinger af tilstødende er allerede vist i figuren. Derfor er det forenklede udtryk for næste tilstand Q(t + 1)
$Q\left ( t+1 \right )=S+{R}’Q\left ( t \right )$
D flip-flop
D flip-flop fungerer kun med positive clockovergange eller negative clockovergange. Hvorimod D latch opererer med et enable-signal. Det betyder, at udgangen af D-flipflop er ufølsom over for ændringer i indgangen D, bortset fra aktiv overgang af ur-signalet. Kredsløbsdiagrammet for D-flip-flop er vist i følgende figur.
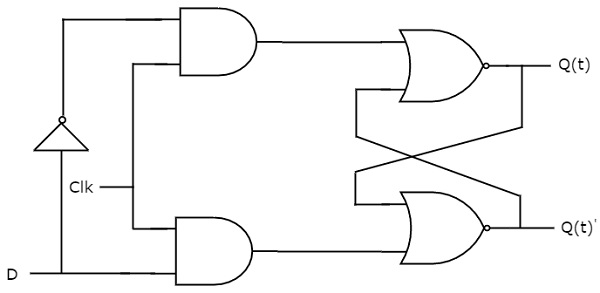
Dette kredsløb har en enkelt indgang D og to udgange Q(t) & Q(t)’. D flip-flop fungerer på samme måde som D Latch. Men denne flip-flop påvirker kun udgangene, når der påføres en positiv overgang af klokkesignalet i stedet for aktiv enable.
Den følgende tabel viser tilstandstabellen for D-flip-flop.
| D | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Derfor, D-flipflop holder altid de oplysninger, som er tilgængelige på dataindgangen D ved tidligere positiv overgang af ur-signalet. Ud fra ovenstående tilstandstabel kan vi direkte skrive ligningen for næste tilstand som
Q(t + 1) = D
Næste tilstand for D-flipflop er altid lig med dataindgangen, D for hver positiv overgang af klokkesignalet. Derfor kan D-flipflops anvendes i registre, skiftregistre og nogle af tællerne.
JK-flipflop
JK-flipflop er den modificerede version af SR-flipflop. Den fungerer kun med positive clockovergange eller negative clockovergange. Kredsløbsdiagrammet for JK-flip-flop er vist i følgende figur.
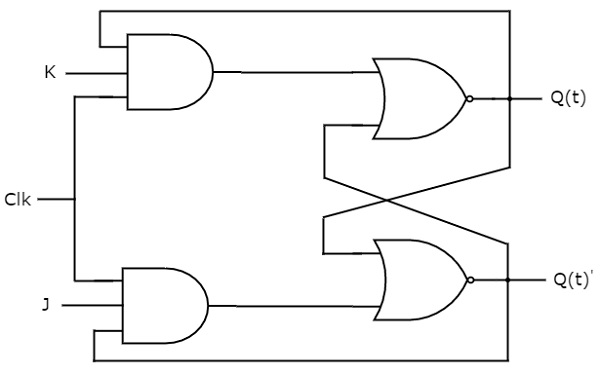
Dette kredsløb har to indgange J & K og to udgange Q(t) & Q(t)’. JK-flipflop fungerer på samme måde som SR-flipflop. Her betragtes SR-flipflopens indgange som S = J Q(t)’ og R = KQ(t)’ for at udnytte den modificerede SR-flipflop til 4 kombinationer af indgange.
Den følgende tabel viser tilstandstabellen for JK-flipflop.
| K | |||
|---|---|---|---|
| 0 | 0 | Q(t) | |
| 0 | |||
| 0 | 1 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 | Q(t)’ |
Her, Q(t) & Q(t + 1) er henholdsvis nuværende tilstand & næste tilstand. JK-flipflop kan således anvendes til en af disse fire funktioner såsom Hold, Reset, Set & Complement of present state baseret på indgangsbetingelserne, når der anvendes en positiv overgang af ur-signalet. Følgende tabel viser den karakteristiske tabel for JK-flipflop.
| På nuværende indgange | På nuværende tilstand | |||
|---|---|---|---|---|
| J | K | Q(t) | Q(t+1) | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 0 |
Ved anvendelse af tre variable K-kort, kan vi få det forenklede udtryk for den næste tilstand, Q(t + 1). K-Map med tre variabler for næste tilstand, Q(t + 1), er vist i følgende figur.
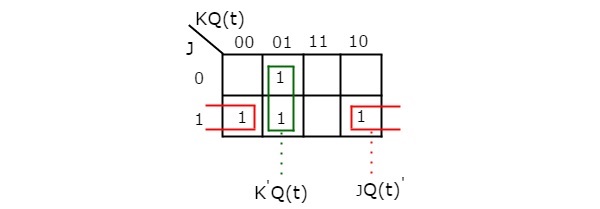
De maksimale mulige grupperinger af tilstødende er allerede vist i figuren. Derfor er det forenklede udtryk for næste tilstand Q(t+1)
$$$Q\left ( t+1 \right )=J{Q\left ( t \right )}’+{K}’Q\left ( t \right )$$
T flip-flop
T flip-flop er den forenklede udgave af JK flip-flop. Det opnås ved at forbinde den samme indgang “T” til begge indgange i JK-flipflop. Den fungerer kun med positive clockovergange eller negative clockovergange. Kredsløbsdiagrammet for T-flip-flop er vist i følgende figur.
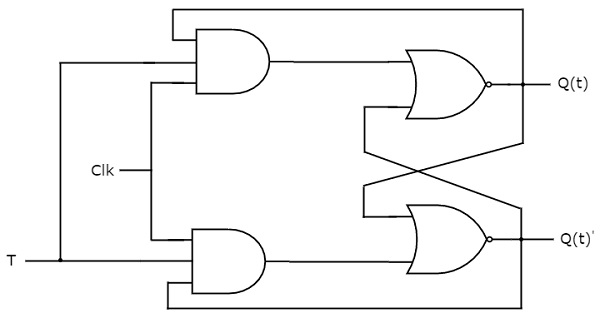
Dette kredsløb har en enkelt indgang T og to udgange Q(t) & Q(t)’. T-flipflopets funktion er den samme som JK-flipflopets. Her betragtes JK-flipflopens indgange som J = T og K = T for at udnytte den modificerede JK-flipflop til to kombinationer af indgange. Vi har således udelukket de to andre kombinationer af J & K, for hvilke disse to værdier supplerer hinanden i T-flip-flop.
Den følgende tabel viser tilstandstabellen for T-flip-flop.
| D | Q(t + 1) |
|---|---|
| 0 | Q(t) |
| 1 | Q(t)’ |
Her, Q(t) & Q(t + 1) er henholdsvis nuværende tilstand & næste tilstand. T-flipflop kan således anvendes til en af disse to funktioner som f.eks. Hold, & Komplement af den nuværende tilstand baseret på indgangsbetingelserne, når der anvendes en positiv overgang af klokkesignalet. Følgende tabel viser den karakteristiske tabel for T-flip-flop.
| Present State | |||
|---|---|---|---|
| T | Q(t) | Q(t + 1) | |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
Fra ovenstående karakteristiske tabel, kan vi direkte skrive den næste tilstandsligning som
$$$Q\left ( t+1 \right )={T}’Q\left ( t \right )+TQ{\left ( t \right )}’$$$
$$$$\Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$$
Det output af T flip-flop skifter altid for hver positiv overgang af klokkesignalet, når indgangen T forbliver på logisk høj (1). Derfor kan T-flip-flop anvendes i tællere.
I dette kapitel har vi implementeret forskellige flip-flops ved at tilvejebringe krydskobling mellem NOR-gates. På samme måde kan du implementere disse flip-flops ved hjælp af NAND-gates.