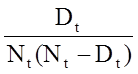Der er flere forskellige måder at estimere en overlevelsesfunktion
eller en overlevelseskurve på. Der findes en række populære parametriske metoder, der anvendes til at modellere overlevelsesdata, og de adskiller sig fra hinanden med hensyn til de antagelser, der gøres om fordelingen af overlevelsestider i populationen. Nogle populære fordelinger omfatter eksponentiel-, Weibull-, Gompertz- og log-normalfordelinger.2 Den måske mest populære er den eksponentielle fordeling, som antager, at en deltagers sandsynlighed for at blive ramt af den pågældende begivenhed er uafhængig af, hvor længe den pågældende person har været begivenhedsfri. Andre fordelinger gør forskellige antagelser om sandsynligheden for, at en person udvikler en begivenhed (dvs. at den kan stige, falde eller ændre sig over tid). Yderligere oplysninger om parametriske metoder til overlevelsesanalyse findes i Hosmer og Lemeshow og Lee og Wang1,3.
Vi fokuserer her på to ikke-parametriske metoder, som ikke gør nogen antagelser om, hvordan sandsynligheden for, at en person udvikler begivenheden, ændrer sig over tid. Ved hjælp af ikke-parametriske metoder estimerer og plotter vi overlevelsesfordelingen eller overlevelseskurven. Overlevelseskurver plottes ofte som trinfunktioner, som vist i figuren nedenfor. Tiden er vist på X-aksen, og overlevelsen (andelen af personer i risiko) er vist på Y-aksen. Bemærk, at den procentdel af deltagerne, der overlever, ikke altid svarer til den procentdel, der er i live (hvilket forudsætter, at det interessante udfald er døden). “Overlevelse” kan også referere til den andel, der er fri for en anden udfaldsbegivenhed (f.eks. procentdel fri for MI eller hjerte-kar-sygdom), eller det kan også repræsentere den procentdel, der ikke oplever et sundt udfald (f.eks. kræft-remission).
Survival Function
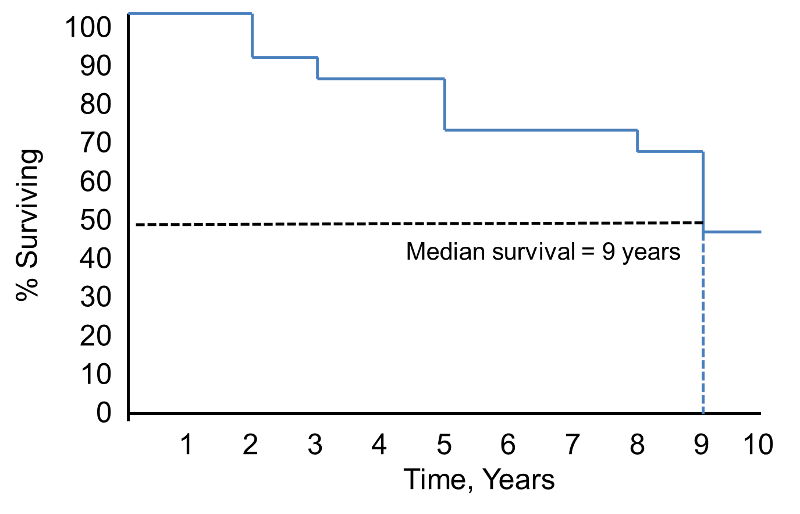
Bemærk, at overlevelsessandsynligheden er 100 % i 2 år og derefter falder til 90 %. Medianoverlevelsen er 9 år (dvs. 50 % af befolkningen overlever 9 år; se stiplede linjer).
Eksempel:
Opmærksomheden henledes på en lille prospektiv kohorteundersøgelse, der er designet til at undersøge tiden til døden. Undersøgelsen omfatter 20 deltagere, der er 65 år og derover; de indskrives i løbet af en 5-årig periode og følges i op til 24 år, indtil de dør, undersøgelsen slutter, eller de falder ud af undersøgelsen (tabt til opfølgning). Dataene er vist nedenfor. I undersøgelsen er der 6 dødsfald og 3 deltagere med fuldstændig opfølgning (dvs. 24 år). De resterende 11 har mindre end 24 års opfølgning på grund af sen tilmelding eller tab af opfølgning.
|
Deltagerens identifikationsnummer |
Dødsår |
År af sidste kontakt |
|---|---|---|
|
1 |
|
24 |
|
2 |
3 |
|
|
3 |
|
11 |
|
4 |
|
19 |
|
5 |
|
24 |
|
6 |
|
13 |
|
7 |
14 |
|
|
8 |
|
2 |
|
9 |
|
18 |
|
10 |
|
17 |
|
11 |
|
24 |
|
12 |
|
21 |
|
13 |
|
12 |
|
14 |
1 |
|
|
15 |
|
10 |
|
16 |
23 |
|
|
17 |
|
6 |
|
18 |
5 |
|
|
19 |
|
9 |
|
20 |
17 |
|
Livstabel (aktuarmæssig tabel)
En måde at sammenfatte deltagernes erfaringer på er med en livstabel, eller en aktuarmæssig tabel. Livstabeller anvendes ofte i forsikringsbranchen til at anslå den forventede levetid og til at fastsætte præmier. Vi fokuserer på en bestemt type livstabel, der anvendes i vid udstrækning i biostatistiske analyser, kaldet en kohorte-livetabel eller en opfølgende livstabel. Opfølgningslivstabellen opsummerer deltagernes erfaringer i løbet af en foruddefineret opfølgningsperiode i en kohorteundersøgelse eller i et klinisk forsøg indtil tidspunktet for den pågældende begivenhed eller afslutningen af undersøgelsen, alt efter hvad der kommer først.
For at konstruere en livstabel organiserer vi først opfølgningstiderne i intervaller med lige store mellemrum. I tabellen ovenfor har vi en maksimal opfølgning på 24 år, og vi overvejer 5-årsintervaller (0-4, 5-9, 10-14, 15-19 og 20-24 år). Vi summerer antallet af deltagere, der er i live ved begyndelsen af hvert interval, antallet af deltagere, der dør, og antallet af deltagere, der censureres i hvert interval.
|
Interval i år |
Antal i live ved begyndelsen af intervallet |
Antal døde i løbet af intervallet |
Antal censureret |
|---|---|---|---|
|
0-4 |
20 |
2 |
1 |
|
5-9 |
17 |
1 |
2 |
|
10-14 |
14 |
1 |
4 |
|
15-19 |
9 |
1 |
3 |
|
20-24 |
5 |
1 |
4 |
Vi anvender følgende notation i vores analyse af livstabellen. Vi definerer først notationen og bruger den derefter til at konstruere livstabellen.
- Nt = antal deltagere, der er begivenhedsfri og anses for at være i risiko i løbet af interval t (f.eks, i dette eksempel antallet af levende, da vores udfald af interesse er død)
- Dt = antal deltagere, der dør (eller lider den begivenhed af interesse) i løbet af interval t
- Ct = antal deltagere, der er censureret i løbet af interval t Nt* = det gennemsnitlige antal deltagere i risiko i løbet af interval t
- Nt* = det gennemsnitlige antal deltagere i risiko i løbet af interval t [Ved konstruktion af aktuarmæssige livstabeller foretages ofte følgende forudsætninger: For det første antages de interessante hændelser (f.eks. dødsfald) at indtræffe i slutningen af intervallet, og censurerede hændelser antages at indtræffe ensartet (eller jævnt) i hele intervallet. Der foretages derfor ofte en justering af Nt for at afspejle det gennemsnitlige antal deltagere i risiko i løbet af intervallet, Nt*, som beregnes som følger: Nt* = Nt-Ct/2 (dvs, vi trækker halvdelen af de censurerede hændelser fra).
- qt = andelen, der dør (eller rammes af en hændelse) i løbet af interval t, qt = Dt/Nt*
- pt = andelen, der overlever (forbliver begivenhedsfri) interval t, pt = 1-qt
- St, andelen, der overlever (eller forbliver begivenhedsfri) efter interval t; dette kaldes undertiden den kumulative overlevelsessandsynlighed, og den beregnes på følgende måde: For det første defineres andelen af deltagere, der overlever efter tidspunkt 0 (starttidspunktet), som S0 = 1 (alle deltagere er i live eller begivenhedsfri på tidspunktet nul eller undersøgelsens start). Andelen, der overlever efter hvert efterfølgende interval, beregnes ved hjælp af principperne for betinget sandsynlighed, som blev introduceret i modulet om sandsynlighed. Konkret er sandsynligheden for, at en deltager overlever efter interval 1, S1 = p1. Sandsynligheden for, at en deltager overlever efter interval 2, betyder, at vedkommende skulle overleve efter interval 1 og gennem interval 2: S2 = P(overleve efter interval 2) = P(overleve gennem interval 2)*P(overleve efter interval 1), eller S2 = p2*S1. Generelt gælder, at St+1 = pt+1*St.
Formatet for den opfølgende livstabel er vist nedenfor.
For det første interval, 0-4 år: På tidspunkt 0, starten af det første interval (0-4 år), er der 20 deltagere i live eller i risiko. To deltagere dør i intervallet, og 1 deltager censureres. Vi anvender korrektionen for antallet af censurerede deltagere i dette interval for at opnå Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. Beregningerne af de resterende kolonner er vist i tabellen. Sandsynligheden for, at en deltager overlever efter 4 år, eller efter det første interval (ved at bruge den øvre grænse af intervallet til at definere tiden), er S4 = p4 = 0,897.
For det andet interval, 5-9 år: Antallet af risikofolk er antallet af risikofolk i det foregående interval (0-4 år) minus dem, der dør og censureres (dvs. Nt = Nt-1-Dt-1-Dt-1-Ct-1 = 20-2-1 = 17). Sandsynligheden for, at en deltager overlever efter 9 år, er S9 = p9*S4 = 0,937*0,897 = 0,840.
|
Interval i år |
Antal i risiko i løbet af intervallet, Nt |
Gennemsnitligt antal i risiko i løbet af intervallet, Nt* |
Antal af dødsfald i løbet af intervallet, Dt |
Gået tabt til opfølgning, Ct |
Andel, der dør under intervallet, qt |
Among Those at Risk, Proportion Surviving Interval, pt |
Sandsynlighed for overlevelse St |
|
|---|---|---|---|---|---|---|---|---|
|
0-4 |
20 |
20 |
20-(1/2) = 19.5 |
2 |
1 |
2/19.5 = 0.103 |
1-0.103 = 0.897 |
1(0.897) = 0.897 |
|
5-9 |
17 |
17-(2/2) = 16.0 |
1 |
2 |
1/16 = 0.063 |
1-0.063 = 0.937 |
(0,897)(0,937)=0,840 |
Den komplette opfølgende livstabel er vist nedenfor.
|
Interval i år |
Antal i risiko i intervallet, Nt |
Gennemsnitligt antal i risiko i intervallet, Nt* |
Antal af dødsfald i løbet af intervallet, Dt |
Gået tabt til opfølgning, Ct |
Andel, der dør under intervallet, qt |
blandt dem, der er i risiko, Andel, der overlever Interval, pt |
Sandsynlighed for overlevelse St |
|---|---|---|---|---|---|---|---|
|
0-4 |
20 |
19.5 |
2 |
1 |
0.103 |
0.897 |
0.897 |
|
5-9 |
17 |
16.0 |
1 |
2 |
0.063 |
0.937 |
0.840 |
|
10-14 |
14 |
12.0 |
1 |
4 |
0.083 |
0.917 |
0.770 |
|
15-19 |
9 |
7.5 |
1 |
3 |
0.133 |
0.867 |
0.668 |
|
20-24 |
5 |
3.0 |
1 |
4 |
0.333 |
0,667 |
0,446 |
Denne tabel anvender den aktuarmæssige metode til at konstruere opfølgningslivstabellen, hvor tiden er opdelt i intervaller med lige store mellemrum.
Kaplan-Meier (produktgrænse)-tilgang
Et problem med den ovenfor viste tilgang til livstabellen er, at overlevelsessandsynlighederne kan ændre sig afhængigt af, hvordan intervallerne er organiseret, især med små stikprøver. Kaplan-Meier-metoden, også kaldet produktgrænse-metoden, er en populær metode, der løser dette problem ved at genvurdere overlevelsessandsynligheden, hver gang en begivenhed indtræffer.
En hensigtsmæssig anvendelse af Kaplan-Meier-metoden hviler på den antagelse, at censurering er uafhængig af sandsynligheden for at udvikle den pågældende begivenhed, og at overlevelsessandsynlighederne er sammenlignelige for deltagere, der rekrutteres tidligt og senere i undersøgelsen. Når man sammenligner flere grupper, er det også vigtigt, at disse antagelser er opfyldt i hver enkelt sammenligningsgruppe, og at f.eks. censurering ikke er mere sandsynlig i én gruppe end i en anden.
I nedenstående tabel anvendes Kaplan-Meier-metoden til at præsentere de samme data, som blev præsenteret ovenfor ved hjælp af livstabelmetoden. Bemærk, at vi starter tabellen med Tid=0 og Overlevelsessandsynlighed = 1. På tidspunktet 0 (baseline eller starten af undersøgelsen) er alle deltagere i risiko, og overlevelsessandsynligheden er 1 (eller 100 %). Med Kaplan-Meier-metoden beregnes overlevelsessandsynligheden ved hjælp af St+1 = St*((Nt+1-Dt+1)/Nt+1). Bemærk, at beregningerne ved hjælp af Kaplan-Meier-metoden svarer til beregningerne ved hjælp af den aktuarmæssige livstabelmetode. Den væsentligste forskel er tidsintervallerne, dvs. at vi med den aktuarmæssige livstabellemetode betragter intervaller med lige store intervaller, mens vi med Kaplan-Meier-metoden anvender observerede hændelsestidspunkter og censoreringstidspunkter. Beregningerne af overlevelsessandsynlighederne er beskrevet i detaljer i de første par rækker i tabellen.
Livstidstabellen ved hjælp af Kaplan-Meier-metoden
|
Tid, År |
Antal i risiko Nt |
Antal dødsfald Dt |
Antal censureret Ct |
Sandsynlighed for overlevelse St+1 = St*((Nt+1-Dt+1)/Nt+1) |
||
|---|---|---|---|---|---|---|
|
0 |
20 |
|
|
|
|
1 |
|
1 |
20 |
1 |
|
1*((20-1)/20) = 0.950 |
||
|
2 |
19 |
|
1 |
0.950*((19-0)/19)=0.950 |
||
|
3 |
18 |
1 |
|
0.950*((18-1)/18) = 0.897 |
||
|
5 |
17 |
1 |
|
0.897*((17-1)/17) = 0.844 |
||
|
6 |
16 |
|
1 |
0.844 |
||
|
9 |
15 |
|
1 |
0.844 |
||
|
10 |
14 |
|
1 |
0.844 |
||
|
11 |
13 |
|
1 |
0.844 |
||
|
12 |
12 |
|
1 |
0.844 |
||
|
13 |
11 |
|
1 |
0.844 |
||
|
14 |
10 |
1 |
|
0.760 |
||
|
17 |
9 |
1 |
1 |
0.676 |
||
|
18 |
7 |
|
1 |
0.676 |
||
|
19 |
6 |
|
1 |
0.676 |
||
|
21 |
5 |
|
1 |
0.676 |
||
|
23 |
4 |
1 |
|
0.507 |
||
|
24 |
3 |
|
3 |
3 |
0.507 |
Med store datasæt er disse beregninger trættende. Disse analyser kan imidlertid genereres af statistiske beregningsprogrammer som SAS. Excel kan også bruges til at beregne overlevelsessandsynlighederne, når dataene er organiseret efter tidspunkter, og antallet af hændelser og censurerede tidspunkter er opsummeret.
Fra livstabellen kan vi fremstille en Kaplan-Meier-overlevelseskurve.
Kaplan-Meier-overlevelseskurve for ovenstående data
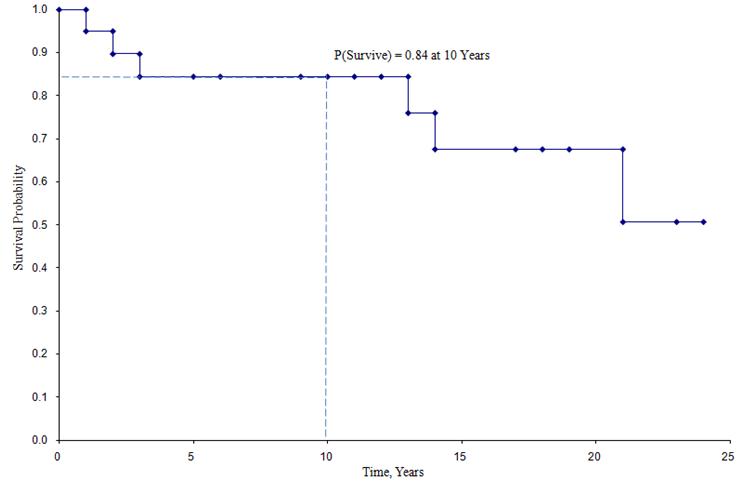
I den ovenfor viste overlevelseskurve repræsenterer symbolerne hvert hændelsestidspunkt, enten et dødsfald eller et censureret tidspunkt. Ud fra overlevelseskurven kan vi også estimere sandsynligheden for, at en deltager overlever efter 10 år, ved at lokalisere 10 år på X-aksen og læse op og over på Y-aksen. Andelen af deltagere, der overlever efter 10 år, er 84 %, og andelen af deltagere, der overlever efter 20 år, er 68 %. Medianoverlevelsen anslås ved at placere 0,5 på Y-aksen og læse over og ned til X-aksen. Medianoverlevelsen er ca. 23 år.
Standardfejl og konfidensintervalestimater af overlevelsessandsynligheder
Disse estimater af overlevelsessandsynlighederne på bestemte tidspunkter og medianoverlevelsestiden er punktestimater og bør fortolkes som sådan. Der findes formler til fremstilling af standardfejl og estimater af konfidensintervaller for overlevelsessandsynligheder, som kan genereres med mange statistiske datapakker. En populær formel til at estimere standardfejlen for overlevelsesestimaterne kaldes Greenwoods5 formel og er som følger:
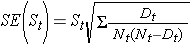
Mængden 
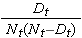summeres for antal i risiko (Nt) og antal dødsfald (Dt), der forekommer gennem det pågældende tidspunkt (dvs. kumulativt, på tværs af alle tidspunkter før det pågældende tidspunkt, jf. eksemplet i tabellen nedenfor). Der beregnes standardfejl for overlevelsesestimaterne for dataene i nedenstående tabel. Bemærk, at den sidste kolonne viser mængden 1,96*SE(St), som er fejlmargenen og anvendes til beregning af estimaterne for 95 % konfidensintervallet (dvs. St ± 1,96 x SE(St)).
Standardfejl for overlevelsesestimater
|
Tid, År |
Antal i risiko Nt |
Antal dødsfald Dt |
Oplevelsestid Sandsynlighed St |
|
|
|
1.96*SE (St) |
|
|---|---|---|---|---|---|---|---|---|
|
0 |
20 |
|
|
1 |
|
|
|
|
|
1 |
20 |
1 |
0.950 |
0.003 |
0.003 |
0.049 |
0.096 |
|
|
2 |
19 |
|
0.950 |
0.000 |
0.003 |
0.049 |
0.096 |
|
|
3 |
18 |
1 |
0.897 |
0.003 |
0.006 |
0.069 |
0.135 |
|
|
5 |
17 |
1 |
0.844 |
0.004 |
0.010 |
0.083 |
0.162 |
|
|
6 |
16 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
|
9 |
15 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
|
10 |
14 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
|
11 |
13 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
|
12 |
12 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
|
13 |
11 |
|
0.844 |
0.000 |
0.010 |
0.083 |
0.162 |
|
|
14 |
10 |
1 |
0.760 |
0.011 |
0.021 |
0.109 |
0.214 |
|
|
17 |
9 |
1 |
0.676 |
0.014 |
0.035 |
0.126 |
0.246 |
|
|
18 |
7 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
|
19 |
6 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
|
21 |
5 |
|
0.676 |
0.000 |
0.035 |
0.126 |
0.246 |
|
|
23 |
4 |
1 |
0.507 |
0.083 |
0.118 |
0.174 |
0.341 |
|
|
24 |
3 |
|
0.507 |
0,000 |
0,118 |
0,174 |
0,341 |
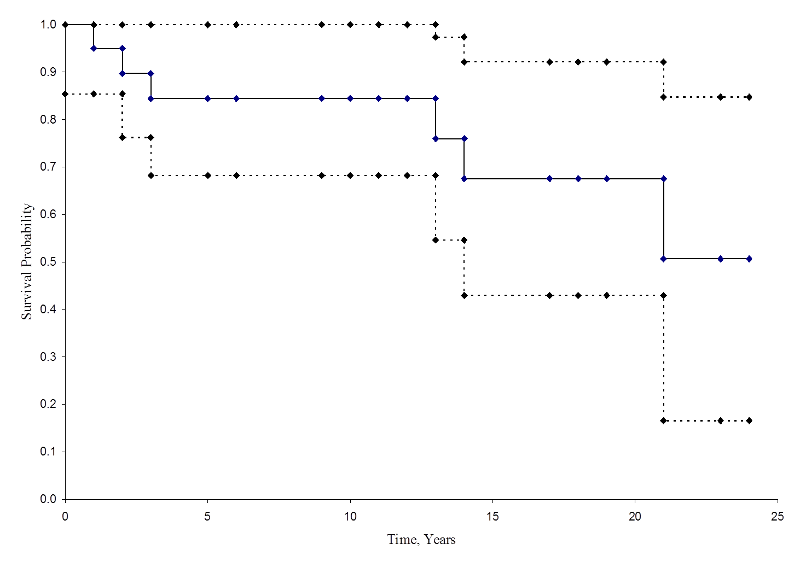
Den nedenstående figur opsummerer estimaterne og konfidensintervallerne i nedenstående figur. Kaplan-Meier-overlevelseskurven er vist som en gennemgående linje, og 95 % konfidensgrænserne er vist som stiplede linjer.
Kaplan-Meier-overlevelseskurve med konfidensintervaller
Kumulative incidenskurver
Nogle undersøgere foretrækker at generere kumulative incidenskurver i modsætning til overlevelseskurver, som viser de kumulative sandsynligheder for at opleve den pågældende hændelse. Kumulativ incidens eller kumulativ fejlsandsynlighed beregnes som 1-St og kan let beregnes ud fra livstabellen ved hjælp af Kaplan-Meier-metoden. De kumulative fejlsandsynligheder for ovenstående eksempel er vist i nedenstående tabel.
Livstidstabel med kumulative fejlsandsynligheder
|
Tid, År |
Antal i risiko Nt |
Antal af dødsfald Dt |
Antal Censureret Ct |
Sandsynlighed for overlevelse St |
Sandsynlighed for svigt 1-St |
||
|---|---|---|---|---|---|---|---|
|
0 |
20 |
|
1 |
1 |
0 |
||
|
1 |
20 |
1 |
|
0.950 |
0.050 |
||
|
2 |
19 |
|
1 |
0.950 |
0.050 |
||
|
3 |
18 |
1 |
|
0.897 |
0.103 |
||
|
5 |
17 |
1 |
|
0.844 |
0.156 |
||
|
6 |
16 |
|
1 |
0.844 |
0.156 |
||
|
9 |
15 |
|
1 |
0.844 |
0.156 |
||
|
10 |
14 |
|
1 |
0.844 |
0.156 |
||
|
11 |
13 |
|
1 |
0.844 |
0.156 |
||
|
12 |
12 |
|
1 |
0.844 |
0.156 |
||
|
13 |
11 |
|
1 |
0.844 |
0.156 |
||
|
14 |
10 |
1 |
|
0.760 |
0.240 |
||
|
17 |
9 |
1 |
1 |
0.676 |
0.324 |
||
|
18 |
7 |
|
1 |
0.676 |
0.324 |
||
|
19 |
6 |
|
1 |
0.676 |
0.324 |
||
|
21 |
5 |
|
1 |
0.676 |
0.324 |
||
|
23 |
4 |
1 |
|
0.507 |
0.493 |
||
|
24 |
3 |
|
3 |
0.507 |
0.493 |
Figuren nedenfor viser den kumulative forekomst af dødsfald for deltagere, der indgik i den ovenfor beskrevne undersøgelse.
Kumulativ incidenskurve
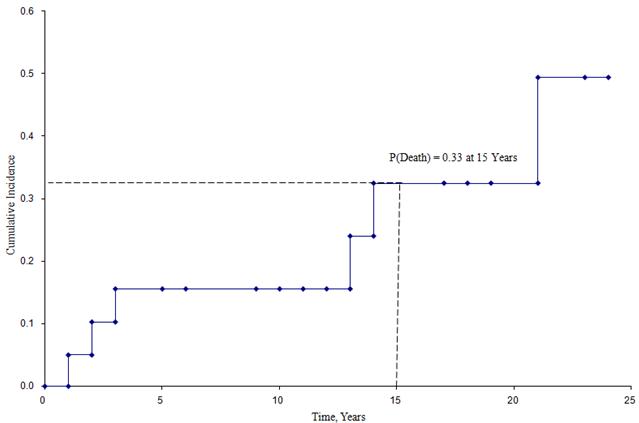
Af denne figur kan vi estimere sandsynligheden for, at en deltager dør inden et bestemt tidspunkt. For eksempel er sandsynligheden for at dø ca. 33 % ved 15 år (se stiplede linjer).
retur til toppen | forrige side | næste side