Af Evan Ma

(Matematik og fysik tutor på The Edge Learning Center)

Den logaritmiske funktion synes at forvirre mange elever, der studerer IB Math SL-programmet. For at forstå den korrekt skal vi definere

hvor , et strengt positivt reelt tal, kaldes basen, og er potensen. Vi kender f.eks. alle følgende udenad:

og så videre. Den logaritmiske funktion gør det omvendt – givet et tal som argument giver den potensen med forbehold af en specificeret base, og derfor er den defineret på følgende måde.

Hvis

så

Det er derfor klart, at

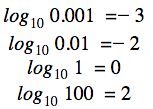
og så videre. Lad os se på andre eksempler, der involverer andre baser:

Lad os besvare følgende spørgsmål som øvelse: (a) , (b) , (c) , (d) . Svarene findes i slutningen af denne blog.

Fra definitionen af logaritme kan vi også se, at hvis vi hæver basen med basis-logaritmen af et reelt tal , får vi tallet tilbage, viz

Du kan prøve at verificere dette ved at bruge din lommeregner for forskellige gyldige baser. Denne identitet er vigtig, når vi forsøger at løse logaritmiske ligninger, som der vil blive givet eksempler på alter.

Nu skal vi se på reglerne for logaritmen. I lighed med definitionen af logaritmen bruger vi lovene for indeks til at udlede reglerne:

1. Logaritmen af et produkt er summen af logaritmerne

Bevis: Sige og , derfor

2. Base- logaritmen af Mr er gange

Bevis: Sige , derfor

3. Logaritme af en kvotient er forskellen af logaritmer

Begrebet: Sig og , derfor

4. Den sidste regel kaldes for grundlagsændringsformlen. Vi vil bruge et eksempel som et redskab til at udlede formlen. Lad os sige, at vi ønsker at vide, hvilken potens 2 skal hæves for at få 50. Da 50 ikke er en heltal potens af 2, er svaret ikke særlig indlysende. Derfor skriver vi

og derfor. For at finde anvender vi f.eks. base-10-logaritme på begge sider af ligningen, da vores lommeregner måske ikke har logaritmetast til base-2:

Korrigeret til 4 betydende cifre er værdien af ca. 5,644. Faktisk kan du verificere dit svar ved at hæve 2 til potensen af 5,644 for at se, at svaret er ca. 50.

For at generalisere problemet, lad os sige, at vi skal finde således, at og base- logaritmen ikke er til vores rådighed, kan vi derfor i stedet bruge base- logaritme i henhold til ligningen

og derfor

Så lad os som eksempel overveje følgende. Lad os antage, at et beløb på 10.000 $ indbetales til en rente på 2,5 % om året, opgjort årligt. Hvor længe skal pengene stå på kontoen, for at de kan vokse til 50.000 dollars?

For at besvare spørgsmålet forsøger vi grundlæggende at finde n således, at

Da min simple videnskabelige lommeregner ikke tillader mig at angive en base på 1.025 for den logaritmiske nøgle, bliver jeg nødt til at stole på formlen for ændring af basen og bruge base-10, og dermed

Da renterne rentesættes årligt, vil det tage 66 år at vokse mindst 5 gange.

Når vi har udforsket reglerne for logaritmer, introducerer vi den naturlige logaritmefunktion, eller . Den er base-, hvor er det eminente irrationale tal ≈2,71828 og hvis betydning inden for naturvidenskab og matematik ikke kan understreges nok. Derfor defineres base-logaritme som følger:

Hvis

så

Næst skal vi se på to eksempler, hvor der begås almindelige fejl ved løsning af ligninger med logaritmer. Prøv at se, om du kan identificere fejlen.

Hvor er fejlen? Se nærmere efter. I det andet trin kan man naturligvis ikke “dele” logaritmen på tværs af additionstegnet. Husk, at man kun kan “splitte” en logaritme op i en sum, hvis logaritmen anvendes på et produkt og ikke på en sum. De korrekte trin er derfor som følger:

Nu skal vi se på følgende eksempel og se, om du kan identificere fejlen:

Hvor er fejlen? Ja, den er i det andet trin – en kvotient af logaritmer er naturligvis ikke logaritmen af kvotienten. Vi kan i stedet bruge formlen for ændring af basen til at forenkle det første trin på følgende måde:

Slutteligt vil vi illustrere, hvordan vi kan bruge logaritmereglerne til at løse følgende:

Du vil måske bemærke, at den ukendte optræder som base og som variabel i logaritmens argument. Hvordan kan vi løse ? Metoden afhænger stadig af, at man anvender logaritmens regler konsekvent. Først hæver vi begge sider som potenser af basen , og dermed

Du husker måske fra definitionen af logaritmen, at venstre side blot bliver argumentet for logaritmen, og derfor

Gennem at omarrangere ovenstående ligning skal vi løse

Og da vi bemærker, at dette ligner en kvadratisk i , løser vi på følgende måde:

Nu, hvor er den negative rod? Da også er logaritmens base, afvises den negative rod derfor som en løsning. Derfor er det endelige svar.

Ved gennemgang af ovenstående eksempler kan du se, at det slet ikke er svært at løse en tilsyneladende vanskelig logaritmisk ligning – man skal blot anvende logaritmereglerne konsekvent, og så kan man få den korrekte løsning.

Svar på spørgsmål: (a) 2 (b) 3 (c) -3 (d) -2.