Kolmogorov-Smirnov-test
K-S-testen er en test for god tilpasning, der anvendes til at vurdere ensartetheden af et sæt datafordelinger. Den blev udviklet som reaktion på manglerne ved chi-kvadrat-testen, som kun giver præcise resultater for diskrete, binnedistributioner. K-S-testen har den fordel, at den ikke forudsætter nogen formodning om binning af de datasæt, der skal sammenlignes, hvilket fjerner den arbitrære karakter og det tab af information, der følger med udvælgelsen af binninger.
Inden for statistik er K-S-testen den accepterede test til måling af forskelle mellem kontinuerlige datasæt (ikke-binned datafordelinger), som er en funktion af en enkelt variabel. Denne forskelsmåling, K-S \(D\)-statistikken, er defineret som den maksimale værdi af den absolutte forskel mellem to kumulative fordelingsfunktioner. Den ensidige K-S-test anvendes til at sammenligne et datasæt med en kendt kumulativ fordelingsfunktion, mens den dobbeltsidede K-S-test sammenligner to forskellige datasæt. Hvert datasæt giver en anden kumulativ fordelingsfunktion, og dens betydning ligger i dens forhold til den sandsynlighedsfordeling, som datasættet er udtrukket fra: sandsynlighedsfordelingsfunktionen for en enkelt uafhængig variabel \(x\) er en funktion, der tildeler hver værdi af \(x\) en sandsynlighed. Den sandsynlighed, som den specifikke værdi \(x_{i}\) antages at have, er værdien af sandsynlighedsfordelingsfunktionen ved \(x_{i}\) og betegnes \(P(x_{i})\).Den kumulative fordelingsfunktion er defineret som den funktion, der angiver brøkdelen af datapunkter til venstre for en given værdi \(x_{i}\), \(P(x <x_{i})\); den repræsenterer sandsynligheden for, at \(x\) er mindre end eller lig med en bestemt værdi \(x_{i}\).
For at sammenligne to forskellige kumulative fordelingsfunktioner \(S_{N1}(x)\) og \(S_{N2}(x)\) er K-S-statistikken således
D = max|S_N1(x) – S_N2(x)|
hvor \(S_{N}(x)\) er den kumulative fordelingsfunktion for den sandsynlighedsfordeling, hvorfra et datasæt med \(N\) hændelser er udtrukket. Hvis \(N\) ordnede hændelser befinder sig på datapunkterne \(x_{i}\), hvor \(i = 1, \ldots, N\), så
S_N(x_i) = (i-N)/N
hvor datamaterialet \(x\) er sorteret i stigende orden. Der er tale om en trinfunktion, der stiger med \(1/N\) ved værdien af hvert ordnet datapunkt.
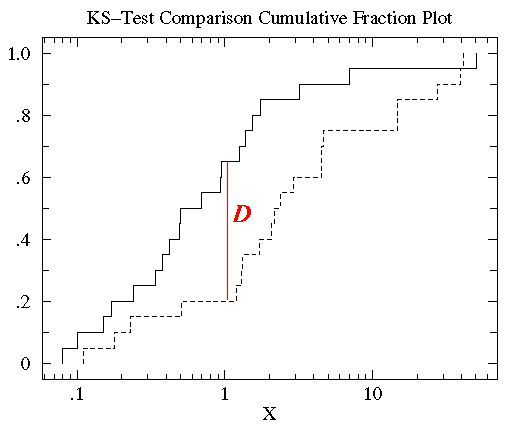
Kirkman, T.W. (1996) Statistists to Use.
http://www.physics.csbsju.edu/stats/
Til vores formål er de to fordelinger, der sammenlignes, den målte fordeling af ankomsttider og den akkumulerede brøkdel på det forløbstidinterval, der er gået. Hvis nulhypotesen (ingen variabilitet) holder, får vi 50 % af dine hændelser i 50 % af den passerede tid, og \(D\)-statistikken bør fordele sig i overensstemmelse med Kolmogorov-fordelingen for mange realiseringer af fordelingen af ankomsttider. Den sandsynlighed, som testen giver, er således \(p_{KS} = 1 – \alpha\), hvor \(\alpha\) er sandsynligheden (i henhold til Kolmogorov-fordelingen) for, at værdien af \(D\) er større eller lig med den målte værdi. En lille værdi af \(p_{KS}\) indikerer derfor, at der er overensstemmelse med nulhypotesen, mens en stor værdi af \(p_{KS}\) indikerer, at intervallet mellem begivenhederne ikke er konstant, og at der derfor kan udledes variabilitet.