6.3 Belief Networks

Begrebet betinget uafhængighed kan bruges til at give en kortfattet repræsentation af mange domæner. Idéen er, at der, givet en tilfældig variabel X, kan findes et lille sæt variabler, som direkte påvirker variablens værdi i den forstand, at X er betinget uafhængig af andre variabler, når værdierne for de direkte påvirkende variabler er givet. Sættet af lokalt påvirkende variabler kaldes Markov-tæppet. Denne lokalitet er det, der udnyttes i et trosnetværk. Et trosnetværk er en rettet model for betinget afhængighed mellem et sæt tilfældige variabler. Den præcise angivelse af betinget uafhængighed i et belief network tager hensyn til retningsbestemtheden.

For at definere et belief network skal man starte med et sæt tilfældige variabler, der repræsenterer alle modellens egenskaber. Antag, at disse variabler er {X1,…,Xn}.Vælg derefter en samlet rækkefølge af variablerne, X1,…,Xn.

Kædereglen (forslag 6.3) viser, hvordan man nedbryder en konjunktion i betingede sandsynligheder:

P(X1=v1∧X2=v2∧—∧Xn=vn)
	=	∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).

Og, med hensyn til tilfældige variabler og sandsynlighedsfordelinger,

P(X1, X2,—, Xn)

=

∏i=1n P(Xi|X1, —, Xi-1).

Definér forældrene til den tilfældige variabel Xi, skrevetparents(Xi), som et minimalt sæt af forgængere til Xi i den samlede rækkefølge, således at de andre forgængere til Xi er betinget uafhængige af Xi givetparents(Xi). Det vil sige, forældre(Xi) ⊆{X1,…,Xi-1}, således at

P(Xi|Xi-1…X1) = P(Xi|forældre(Xi)).

Hvis der findes mere end et minimalt sæt, kan ethvert minimalt sæt vælges som forældre. Der kan kun være mere end ét minimumsæt, når nogle af forløberne er deterministiske funktioner af andre.

Vi kan sætte kædereglen og definitionen af forældre sammen,hvilket giver

P(X1, X2,—, Xn)

=

∏i=1n P(Xi|forældre(Xi))).

Sandsynligheden over alle variablerne, P(X1, X2,—,Xn), kaldes den fælles sandsynlighedsfordeling. Et trosnetværk definerer en faktorisering af den fælles sandsynlighedsfordeling, hvor de betingede sandsynligheder danner faktorer, der ganges sammen.

Et trosnetværk, også kaldet et Bayesiannetværk, er en acyklisk rettet graf (DAG), hvorknuderne er tilfældige variabler. Der er en bue fra hvert element iparents(Xi) til Xi.Tilknyttet trosnetværket er et sæt betingede sandsynlighedsfordelinger – den betingede sandsynlighed for hver variabel givet dens forældre (som omfatter de forudgående sandsynligheder for de variabler, der ikke har nogen forældre).

Så består et trosnetværk af

• en DAG, hvor hver knude er mærket med en tilfældig variabel;
• et domæne for hver tilfældig variabel; og
• et sæt af betingede sandsynlighedsfordelinger, der giver P(X|forældre(X)) for hver variabel X.

Et trosnetværk er acyklisk af konstruktion. Den måde, hvorpå kædereglerne sammensætter konjunktionen, giver rækkefølgen. En variabel kan kun have forgængere som forældre.Forskellige dekompositioner kan resultere i forskellige trosnetværk.

Eksempel 6.10: Lad os antage, at vi ønsker at bruge diagnosticeringsassistenten til at diagnosticere, om der er brand i en bygning på baggrund af støjende sensoroplysninger og muligvis modstridende forklaringer på, hvad der kan være på færde. Agentenmodtager en rapport om, hvorvidt alle er ved at forlade bygningen. Lad os antage, at rapportensensoren er støjende: Nogle gange rapporterer den, at alle forlader bygningen, når der ikke er nogen udvandring (falsk positiv), og nogle gange rapporterer den ikke, når alle forlader bygningen (falsk negativ). Antag, at en brandalarm, der går i gang, kan være årsag til, at folk forlader bygningen, men der er ikke tale om et deterministisk forhold: Enten kan der være tale om manipulation eller brand, som kan påvirke alarmen, og brand får også røg til at stige op fra bygningen.

Sæt, at vi bruger følgende variabler, som alle er boolske, i følgende rækkefølge:

• Sabotage er sandt, når der er saboteret alarmen.
• Brand er sandt, når der er brand.
• Alarm er sandt, når alarmen lyder.
• Røg er sandt, når der er røg.
• Afgang er sandt, hvis der er mange mennesker, der forlader bygningen på én gang.
• Rapport er sandt, hvis der er en rapport fra nogen om, at der er mennesker, der forlader bygningen. Rapport er falsk, hvis der ikke er nogen rapport om, at folk forlader bygningen.

Variablen Rapport angiver sensorens rapport om, at folk forlader bygningen. Disse oplysninger er upålidelige, fordi den person, der afgiver en sådan rapport, kan lave en practicaljoke, eller fordi ingen, der kunne have afgivet en sådan rapport, har været opmærksom. Denne variabel er indført for at muliggøre en konditionering af upålidelige sensordata. Agenten ved, hvad sensoren rapporterer, men har kun upålidelige oplysninger om personer, der forlader bygningen.Som en del af domænet antages følgende betingede uafhængigheder:

• Brand er betinget uafhængig af manipulation (givet ingen andre oplysninger).
• Alarm afhænger af både brand og manipulation. Det vil sige, at vi ikke foretager nogen uafhængighedsantagelser om, hvordan alarmen afhænger af sine forgængere i denne variabelrækkefølge.
• Røg afhænger kun af brand og er betinget uafhængig af manipulation og alarm, når det er givet, om der er brand.
• Lækkerhed afhænger kun af alarm og ikke direkte af brand, manipulation eller røg. Det vil sige, at afgang er betinget uafhængig af de andre variabler givet alarm.
• Rapport afhænger kun direkte af afgang.

Troværdighedsnetværket i figur 6.1 udtrykker disse afhængigheder.

Figur 6.1: Troværdighedsnetværk for rapport om afgang i eksempel 6.10

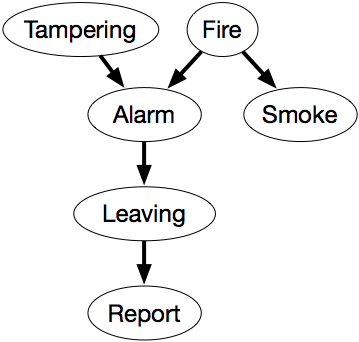
Dette netværk repræsenterer faktoriseringen

P(Sabotage,Brand,Alarm,Røg,Afgang,Rapport)
	=	P(Sabotage) ×P(Brand) ×P(Alarm|Sabotage,Brand)
				×P(Røg|Brand) ×P(Forladelse|Alarm) ×P(Rapport|Førladelse).

Vi skal også definere domænet for hver variabel. Antag, atvariablerne er boolske; det vil sige, at de har domæne {true,false}. Vianvender den lille variant af variablen til at repræsentere den sande værdiog anvender negation for den falske værdi. Således skrives f.eks. Tampering=true som tampering, ogTampering=false skrives som ¬tampering.

I de følgende eksempler antages følgende betingede sandsynligheder:

P(tampering) = 0,02
P(brand) = 0,01
P(alarm | brand ∧tampering) = 0.5
P(alarm | brand ∧¬manipulation) = 0,99
P(alarm | ¬brand ∧manipulation) = 0,85
P(alarm | ¬brand ∧¬manipulation) = 0,0001
P(røg | brand ) = 0,0001
P(røg | brand ) = 0.9
P(røg | ¬brand ) = 0,01
P(afgang | alarm) = 0,88
P(afgang | ¬alarm ) = 0,001
P(rapport | afgang ) = 0,75
P(rapport | ¬afgang ) = 0,75
P(rapport | ¬afgang ) = 0.01

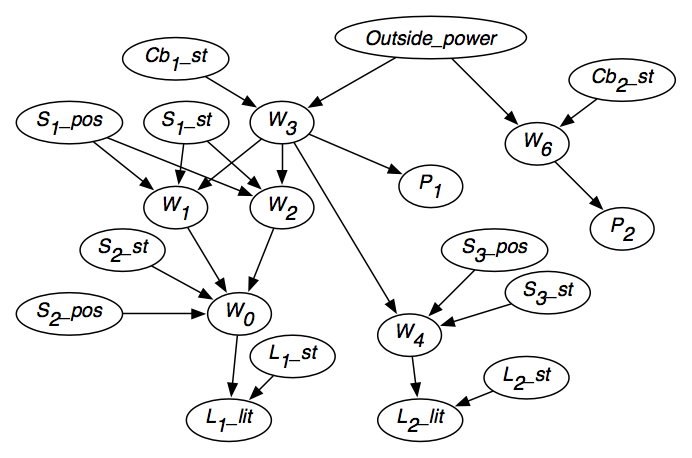
• For hver ledning wi findes der en tilfældig variabel, Wi, meddomæne {live,dead}, som angiver, om der er strøm i ledningen wi. Wi=live betyder, at ledningenwi har strøm. Wi=død betyder, at der ikke er strøm i ledning wi.
• Outside_power med domæne {live,dead} angiver, om der kommer strøm ind i bygningen.
• For hver afbryder si angiver variabel Si_pos positionen forsi. Den har domæne {up,down}.
• For hver afbryder si angiver variablen Si_st afbryderens tilstand for si. Ihar domæne {ok,upside_down,kort,intermitterende,brudt}. Si_st=ok betyder, atafbryder si fungerer normalt. Si_st=upside_down betyder, at afbrydersi er installeret med hovedet nedad. Si_st=kort betyder, at kontakten si er forkortet og fungerer som en ledning. Si_st=brudt betyder, at afbryderen si er brudt og ikke tillader strømmen at strømme.
• For hver afbrydercbi har variablen Cbi_st domænet {on,off}. Cbi_st=on betyder, at strømmen kan strømme gennem cbi, og Cbi_st=off betyder, at strømmen ikke kan strømme gennem cbi.
• For hver lygte li angiver variabel Li_st med domæne {ok,intermitterende,brudt} lygtens tilstand. Li_st=ok betyder, at lyset li lyser, hvis det er strømforsynet, Li_st=intermittent betyder, at lyset li lyser med mellemrum, hvis det er strømforsynet, og Li_st=brudt betyder, at lyset li ikke virker.

Et trosnetværk er en grafisk repræsentation af betinget uafhængighed. uafhængigheden giver os mulighed for at afbilde direkte virkninger inden for grafenog foreskriver, hvilke sandsynligheder der skal angives. Arbitrære posterior-sandsynligheder kan udledes af netværket.

Uafhængighedsantagelsen, der er indlejret i et trosnetværk, er som følger: Hver tilfældig variabel er betinget uafhængig af sine ikkeefterfølgere givet sine forældrene. Det vil sige, at hvis X er en tilfældig variabel med forældre Y1,…, Yn, er alle tilfældige variabler, der ikke er efterkommere af X, betinget uafhængige af X, når Y1,…, Yn er givet:

P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),

hvis R ikke omfatter en efterkommer af X. I denne definition medtager vi X som en efterkommer af sig selv. Den højre side af denne ligning er formen af de sandsynligheder, der er specificeret som en del af trosnetværket.R kan involvere forfædre til X og andre knuder, så længe de ikke er efterkommere af X. Uafhængighedshypotesen siger, at al indflydelse fra variabler, der ikke er efterkommere, er indfanget ved at kende værdien af X’s forældre.

Ofte refererer vi kun til den mærkede DAG som et trosnetværk. Når dette gøres, er det vigtigt at huske, at et domæne for hver variabel og et sæt betingede sandsynlighedsfordelinger også er en del af netværket.

Antallet af sandsynligheder, der skal angives for hver variabel, er eksponentielt i forhold til antallet af forældrene til variablen.Uafhængighedsantagelsen er nyttig, for så vidt som antallet af variabler, der direkte påvirker en anden variabel, er lille. Du bør ordne variablerne, så knuderne har så få forældre som muligt.

Troværdighedsnetværk og kausalitet

Troværdighedsnetværk er ofte blevet kaldt kausalnetværk og er blevet hævdet at være en god repræsentation af kausalitet.Husk, at en kausalmodel forudsiger resultatet af interventioner.Antag, at du har i tankerne en kausalmodel af et domæne, hvor domænet er specificeret i form af et sæt tilfældige variabler. For hvert par tilfældige variabler X1og X2 gælder det, at hvis der er en direkte kausal forbindelse fra X1 til X2 (dvs. hvis et indgreb for at ændre X1 i en eller anden sammenhæng med andre variabler påvirker X2, og dette ikke kan modelleres ved at have en eller anden indgrebsvariabel), skal du tilføje en bue fra X1 til X2. Man ville forvente, at kausalmodellen ville overholde antagelsen om uafhængighed i trosnetværket. Således ville alle konklusionerne i trosnetværket være gyldige.

Du ville også forvente, at en sådan graf ville være acyklisk; du ønsker ikke, at noget til sidst forårsager sig selv. Denne antagelse er rimelig, hvis man overvejer, at de tilfældige variabler repræsenterer bestemte hændelser snarere end hændelsestyper. Overvej f.eks. en årsagskæde, hvor “at være stresset” får dig til at “arbejde ineffektivt”, hvilket igen får dig til at “være stresset”. For at bryde den tilsyneladende cyklus kan vi repræsentere “at være stresset” på forskellige stadier som forskellige tilfældige variabler, der refererer til forskellige tidspunkter. At være stresset i fortiden får dig til ikke at arbejde godt i øjeblikket, hvilket får dig til at være stresset i fremtiden. Variablerne skal opfylde klarhedsprincippet og have en veldefineret betydning. Variablerne bør ikke ses som begivenhedstyper.

Trodsnetværket i sig selv har intet at sige om årsagssammenhæng, og det kan repræsentere ikke-kausal uafhængighed, men det synes særlig velegnet, når der er årsagssammenhæng i et område. Tilføjelse af buer, der repræsenterer lokal kausalitet, har tendens til at give et lille trosnetværk. Trodsnetværket iFigur 6.2 viser, hvordan dette kan gøres for et simpelt domæne.

Akausale netværksmodeller for interventioner. Hvis nogen kunstigt tvinger en variabel til at have en bestemt værdi, vil variablens efterkommere – men ingen andre knuder – blive påvirket. Endelig kan du se, hvordan kausaliteten i trosnetværk hænger sammen med de kausale og evidensmæssige ræsonnementer, der blev diskuteret i afsnit 5.7. Et kausalt trosnetværk kan ses som en aksiomatisering i en kausal retning. Ræsonnement i trosnetværk svarer til at abducere til årsager og derefter at forudsige ud fra disse. Der er en direkte sammenhæng mellem den logisk baserede abduktive opfattelse, der er beskrevet i afsnit 5.7, og trosnetværk: Overbevisningsnetværk kan modelleres som logiske programmer med sandsynligheder over mulige hypoteser. Dette er beskrevet i afsnit 14.3.

Bemærk begrænsningen “hver tilfældig variabel er betinget uafhængig af sine ikkeefterfølgere givet sineforældre” i definitionen af den uafhængighed, der er kodet i et trosnetværk. HvisR indeholder en efterkommer til variabel X, er uafhængighedsantagelsen ikke direkte anvendelig.

Et trosnetværk angiver en fælles sandsynlighedsfordeling, hvorfra vilkårlige betingede sandsynligheder kan udledes. Et netværk kan spørges ved at spørge om den betingede sandsynlighed for enhver variabel, der er betinget af værdierne af andre variabler. Dette sker typisk ved at give observationer af nogle variabler og spørge om en anden variabel.

• 6.3.3.1 Konstruktion af trosnettene