The StatsTest Flow: Forudsigelse >> Kontinuerlig afhængig variabel >> Mere end én uafhængig variabel >> Ingen gentagne målinger >> Én afhængig variabel

Er du ikke sikker på, at dette er den rigtige statistiske metode? Brug arbejdsgangen Vælg din StatsTest til at vælge den rigtige metode.

Hvad er multivariat multipel lineær regression?

Multivariat multipel lineær regression er en statistisk test, der bruges til at forudsige flere udfaldsvariabler ved hjælp af en eller flere andre variabler. Den bruges også til at bestemme det numeriske forhold mellem disse sæt variabler og andre variabler. Den variabel, du ønsker at forudsige, skal være kontinuerlig, og dine data skal opfylde de øvrige antagelser, der er anført nedenfor.

Ansætninger for multivariat multipel lineær regression

Alle statistiske metoder har antagelser. Antagelser betyder, at dine data skal opfylde visse egenskaber, for at resultaterne af den statistiske metode kan være nøjagtige.

Antagelserne for multivariat multipel lineær regression omfatter:

1. Linearitet
2. Ingen outliers
3. Sammenlignende spredning over hele området
4. Normalitet af residualer
5. Ingen multikollinearitet

Lad os dykke ned i hver af disse separat.

Linearitet

De variabler, som du interesserer dig for, skal være lineært relateret til hinanden. Det betyder, at hvis du plotter variablerne, skal du kunne tegne en lige linje, der passer til dataenes form.

Ingen outliers

De variabler, som du interesserer dig for, må ikke indeholde outliers. Lineær regression er følsom over for outliers, dvs. datapunkter, der har usædvanligt store eller små værdier. Du kan se, om dine variabler har outliers ved at plotte dem og observere, om nogle punkter er langt fra alle andre punkter.

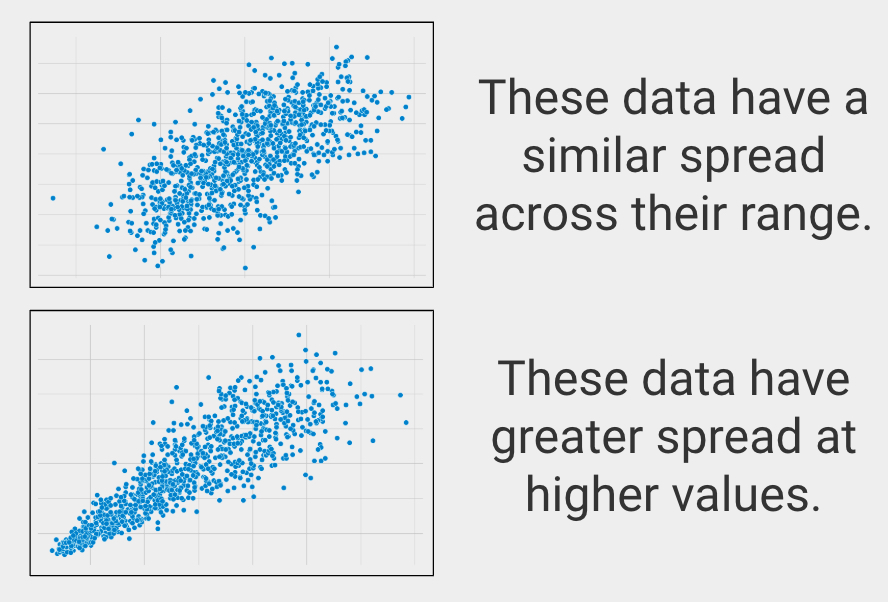
Sammenlignende spredning på tværs af intervallet

I statistikken kaldes dette homoscedasticitet, som beskriver, når variabler har en lignende spredning på tværs af deres intervaller.

Normalitet af residualer

Ordet “residualer” henviser til de værdier, der fremkommer ved at trække de forventede (eller forudsagte) afhængige variabler fra de faktiske værdier. Fordelingen af disse værdier bør svare til en normal (eller klokkekurve) fordelingsform.

Opfyldelse af denne antagelse sikrer, at regressionsresultaterne er lige anvendelige over hele spændvidden af dataene, og at der ikke er nogen systematisk skævhed i forudsigelsen.

Ingen multikollinearitet

Multikollinearitet henviser til det scenarie, hvor to eller flere af de uafhængige variabler er væsentligt korrelerede indbyrdes. Når multikollinearitet er til stede, bliver regressionskoefficienterne og den statistiske signifikans ustabile og mindre troværdige, selv om det ikke påvirker, hvor godt modellen passer til dataene i sig selv.

Hvornår skal man bruge multivariate multipel lineær regression?

Du bør bruge Multivariate Multiple Linear Regression i følgende scenarie:

1. Du ønsker at bruge én variabel i en forudsigelse af flere andre variabler, eller du ønsker at kvantificere det numeriske forhold mellem dem
2. De variabler, du ønsker at forudsige (din afhængige variabel), er kontinuerlige
3. Du har mere end én uafhængig variabel, eller én variabel, som du bruger som en prædiktor
4. Du har ingen gentagne målinger fra den samme observationsenhed
5. Du har mere end én afhængig variabel

Lad os præcisere disse for at hjælpe dig med at vide, hvornår du skal bruge multivariat multipel lineær regression.

Forudsigelse

Du leder efter en statistisk test til at forudsige en variabel ved hjælp af en anden variabel. Dette er et spørgsmål om forudsigelse. Andre typer analyser omfatter undersøgelse af styrken af forholdet mellem to variabler (korrelation) eller undersøgelse af forskelle mellem grupper (forskel).

Kontinuerlig afhængig variabel

Den variabel, du ønsker at forudsige, skal være kontinuerlig. Kontinuerlig betyder, at din variabel af interesse stort set kan antage en hvilken som helst værdi, f.eks. puls, højde, vægt, antal isbarer, du kan spise på 1 minut osv.

Typer af data, der IKKE er kontinuerte, omfatter ordnede data (f.eks. slutplacering i et løb, bedste virksomhedsrangliste osv.), kategoriske data (køn, øjenfarve, race osv.) eller binære data (købt produktet eller ej, har sygdommen eller ej osv.).

Hvis din afhængige variabel er binær, skal du bruge Multipel logistisk regression, og hvis din afhængige variabel er kategorisk, skal du bruge Multinomial logistisk regression eller Lineær diskriminantanalyse.

Mere end én uafhængig variabel

Multivariat multipel lineær regression anvendes, når der er en eller flere prædiktorvariable med flere værdier for hver observationsenhed.

Ingen gentagne målinger

Denne metode er velegnet til det scenarie, hvor der kun er én observation for hver observationsenhed. Observationsenheden er det, der udgør et “datapunkt”, f.eks. en butik, en kunde, en by osv…

Hvis du har en eller flere uafhængige variabler, men de måles for den samme gruppe på flere tidspunkter, skal du bruge en Mixed Effects Model.

Mere end én afhængig variabel

For at køre multivariat multipel lineær regression skal du have mere end én afhængig variabel eller variabel, som du forsøger at forudsige.

Hvis du kun forudsiger én variabel, skal du bruge multipel lineær regression.

Multivariat multipel lineær regression Eksempel

Dependent variabel 1: Omsætning
Dependent variabel 2: Kundetrafik
Independent variabel 1: Dollars brugt på reklame pr. by
Uafhængig variabel 2: Byens befolkning

Nulhypotesen, som er statistisk jargon for, hvad der ville ske, hvis behandlingen ikke gør noget, er, at der ikke er nogen sammenhæng mellem udgifter til reklame og reklame-dollars eller befolkning pr. by. Vores test vil vurdere sandsynligheden for, at denne hypotese er sand.

Vi indsamler vores data, og efter at vi har sikret os, at forudsætningerne for lineær regression er opfyldt, udfører vi analysen.

Denne analyse udfører faktisk multipel lineær regression to gange ved hjælp af begge afhængige variabler. Når vi udfører denne analyse, får vi således betakoefficienter og p-værdier for hvert udtryk i modellen for “indtægter” og i modellen for “kundetrafik”. For enhver lineær regressionsmodel vil du have en betakoefficient, som er lig med skæringspunktet for din lineære regressionslinje (ofte mærket med et 0 som β0). Dette er simpelthen det sted, hvor regressionslinjen krydser y-aksen, hvis du skulle plotte dine data. I tilfælde af multipel lineær regression er der desuden to yderligere flere andre betakoefficienter (β1, β2 osv.), som repræsenterer forholdet mellem de uafhængige og afhængige variabler.

Disse yderligere betakoefficienter er nøglen til at forstå den numeriske sammenhæng mellem dine variabler. I det væsentlige forventes det, at din afhængige variabel for hver enhed (værdi 1) stigning i en given uafhængig variabel vil ændre sig med værdien af den betakoefficient, der er knyttet til den pågældende uafhængige variabel (mens andre uafhængige variabler holdes konstante).

Den p-værdi, der er knyttet til disse yderligere betaværdier, er chancen for at se vores resultater, hvis vi antager, at der faktisk ikke er nogen sammenhæng mellem den pågældende variabel og indtægterne. En p-værdi på mindre end eller lig med 0,05 betyder, at vores resultat er statistisk signifikant, og at vi kan stole på, at forskellen ikke skyldes tilfældigheder alene. For at få en samlet p-værdi for modellen og individuelle p-værdier, der repræsenterer variablernes virkninger på tværs af de to modeller, anvendes ofte MANOVA’er.

Dertil kommer, at denne analyse vil resultere i en R-Squared (R2)-værdi. Denne værdi kan variere fra 0-1 og repræsenterer, hvor godt din lineære regressionslinje passer til dine datapunkter. Jo højere R2-værdien er, jo bedre passer din model til dine data.

Hyppigt stillede spørgsmål

Q: Hvad er forskellen mellem multivariat multipel lineær regression og at køre lineær regression flere gange?
A: De er konceptuelt set ens, da de enkelte modelkoefficienter vil være de samme i begge scenarier. En væsentlig forskel er dog, at signifikanstest og konfidensintervaller for multivariat lineær regression tager højde for de flere afhængige variabler.

Q: Hvordan kører jeg multivariat multipel lineær regression i SPSS, R, SAS eller STATA?
A: Denne ressource er fokuseret på at hjælpe dig med at vælge den rigtige statistiske metode hver gang. Der er mange ressourcer til rådighed, som kan hjælpe dig med at finde ud af, hvordan du kan køre denne metode med dine data:
R-artikel: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/

Hjælp!

Hvis du stadig ikke kan finde ud af noget, er du velkommen til at tage kontakt.