I begyndelsen er det normalt nødvendigt at få en idé om cyklens pV-diagram. Til dette formål vil vi spore kurverne for de isokoriske og adiabatiske processer. Otto cyklussens omtrentlige graf er vist i følgende figur.
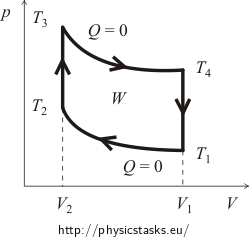
Cyklussens virkningsgrad η er defineret som
\
hvor W er det arbejde, der udføres af gassen i løbet af en cyklus minus det arbejde, der udføres af de ydre kræfter (i diagrammet er det repræsenteret af overfladen af det område, der er defineret af cyklussens linjer!) og Qsup er den varme, der tilføres systemet i løbet af cyklussen.
Arbejdet W kan beregnes ved hjælp af forholdet mellem trykket og volumenet under en adiabatisk ekspansion og kompression (det arbejde, der udføres under en isokorisk proces, er naturligvis nul). I denne opgave vil det dog være bedre at bruge det faktum, at den samlede ændring i den indre energi pr. cyklus skal være lig nul (vi kommer tilbage til samme tilstand som i begyndelsen, derfor forbliver temperaturen og dermed den indre energi den samme!). I henhold til den første termodynamiske lov kan det arbejde, som gassen udfører, udtrykkes som forskellen mellem den tilførte varme Qsup og den afgivne varme Qrel. Formlen for cyklens virkningsgrad er derfor på følgende måde:
\
Først beregner vi den tilførte varme Qsup. Det er klart, at der under den adiabatiske proces ikke sker nogen varmeudveksling, og at der under den isokoriske afkøling frigives varme. Det betyder, at der kun tilføres varme under den isokoriske opvarmning fra temperaturen T2 til temperaturen T3. Mængden af denne varme kan udtrykkes i variablerne stofmængde n i gassen og dens molære varmekapacitet CV på følgende måde:
\
Vi vil udtrykke mængden af den frigjorte varme Qrel på nogenlunde samme måde. Vi ved allerede, at varmen kun frigives under den isokoriske afkøling fra temperaturen T4 tilbage til udgangstemperaturen T1. Det er rigtigt, at:
\
Nu indsætter vi disse formler i formlen for cyklusens virkningsgrad, og vi får straks:
\ \ \
Nu skal vi udtrykke temperaturforskellene ved hjælp af det givne kompressionsforhold
\
og Poissonforholdet κ.
Dertil skal vi bruge ligningen for en idealgas, der gennemgår en adiabatisk proces (Poissons lov) pVκ = C = konst., hvor C er en konstant. Nu vurderer vi trykket ud fra tilstandsligningen for en idealgas
\
som vi indsætter i Poissons lov. Nu overfører vi konstanterne (C og K) til den ene side
\
Nu anvender vi denne Poisson’s lov for begge adiabatiske processer. For den adiabatiske ekspansion får vi relationen
\
Og for den adiabatiske kompression får vi
\
Nu trækker vi den anden ligning fra den første og faktoriserer V1κ – 1 på den ene side og V2κ – 1 på den anden side. Vi får:
\ \ \
Vi kan se, at vi faktisk har formået at udtrykke temperaturforskellene ved hjælp af de givne værdier. Nu indsætter vi denne relation i formlen for virkningsgraden, og vi får den endelige ligning:
\ \ \ \