Tetraeder | Maternidad y todo

Tetraeder

Indholdet af denne side

Hvad er et tetraeder?
Tetraederstykker
Tetraedertal

Tetraeder i Kuben
Ringe af Tetraedre
Tetraedre påInternet

Til hovedsiden “Mathematische Basteleien”

Hvad er et Tetraeder?

Et tetraeder er en tredimensionel figur med fire lige store trekanter. Hvis man løfter tre trekanter op (1), får man tetraederet i oversigt (2). Almindeligvis er den vist i perspektiv (3).

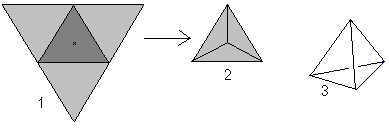
Hvis man ser på ordet tetraeder (tetraeder betyder “med fire flader”), kan man kalde enhver pyramide med en trekant som base for et tetraeder.

Hvertfald er tetraederet den lige, regelmæssige trekantpyramide på denne hjemmeside.

Stykker af tetraedrontoppen
Højde og areal af en sidetrekanten
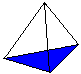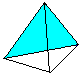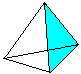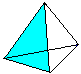
Fire ligesidede trekanter danner et tetraeder.

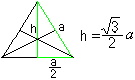…	En trekant er udplukket: De tre højder skærer hinanden i ét punkt som i alle trekanter. Dette er trekantens centrum. Højden kan beregnes ud fra siden a som h=sqr(3)/2*a ved hjælp af pythagoras’ sætning.

Højderne er også medianer og skærer hinanden i forholdet2:1. Det bruges i de følgende beregninger.

Trekantens areal er A=sqr(3)/4*a².

Rumhøjde

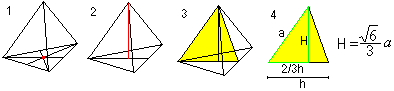
Tetraedrets højde er mellem centrum af grundtrekanten (1) og toppunktet (2). Til beregninger betragter du den såkaldte støttetrekanten (3, gul), som er dannet af en kant og to trekantshøjder. Der er H=sqr(6)/3*a ved hjælp af Pythagoras sætning.
Center, omskreven kugle og indskreven kugle

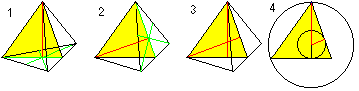
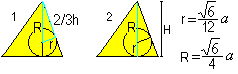Centrum af et tetraeder er skæringspunktet mellem to rumhøjder (1,2,3). Det er tyngdepunkt, centrum for kuglen gennem de fire hjørner og centrum for den største kugle, som stadig passer ind i tetraederet (4).

…	Du får to formler for r og R ved hjælp af den pythagoræiske sætning (1) og H=R+r (2): Der er r=sqr(6)/12a , R=sqr(6)/4a.

Vinkeloverflade

….

…..

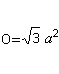Som grundflade og sidefladerne danner overfladenO. Der er O=4*A (trekant) = sqr(3)a².

Rumfang

Tetraediske tal top

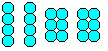……	Hvis man limer 20 kugler til to grupper med fire og to med seks, får man et velkendt puslespil: Man skal danne en pyramide med firestykker.

Der findes mange lignende puslespil.

Tetraeder i terningen øverst
Seks diagonaler på forsiden danner et tetraeder i terningen.
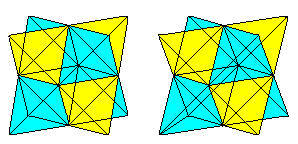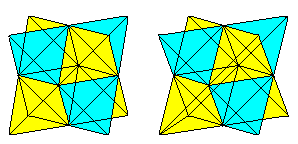
Hvis du kender 3D-synet, kan du tredimensionelt se på følgende to terningpar.

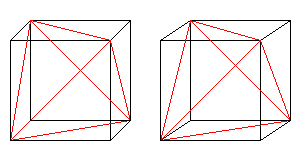
Tetraederets rumfang er den tredje del af kubens rumfang.

Hvis du tegner et andet tetraeder og skæringspunkterne, får du en gennemtrængning af to tetraedre.

Figuren består af fladediagonalerne og forbindelseslinjerne mellem centrumene af de laterale firkanter i den oprindelige terning. De sidste danner et oktaeder.

Ringe af tetraedre top
Du kan lave tetraedre af papir og klistre et lige antal af dem til en ring. Ringen kan hele tiden dreje indad eller udad gennem midten. Det er et smukt stykke legetøj. – Disse ringe kaldes også kaleidocycles.Du kan finde mere på min webside Kaleidocycles.

Tetraedrager på Internettop

Tysk

Christof Weber
Washat dieser Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)

Albert Kluge
Einrotierender Tetraeder als Java-Applet

FAZ
Tetraederpackung:Eins geht noch

Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)

Gerd Müller
Gerd Müller
PlatonischeKörper in Stereodarstellung

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder

ruhr-guide
TetraederBottrop

Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl

Engelsk

Eric W. Weisstein (World of Mathematics)
Tetraeder

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

Joyce Frost and Peg Cagle (mathforum)
AnAmazing, Space Filling, Non-regular Tetrahedron

Wikipedia
Tetraeder,Tetrapod(struktur), Tetrahedralnumber

Skriv et svar Annuller svar