Christian Bohr und das Konzept der kooperativen BindungEdit
Im Jahr 1904 untersuchte Christian Bohr die Bindung von Hämoglobin an Sauerstoff unter verschiedenen Bedingungen. Als er die Sättigung des Hämoglobins mit Sauerstoff als Funktion des Sauerstoffpartialdrucks aufzeichnete, erhielt er eine sigmoidale (oder “S-förmige”) Kurve. Dies bedeutet, dass je mehr Sauerstoff an Hämoglobin gebunden ist, desto leichter kann weiterer Sauerstoff gebunden werden – bis alle Bindungsstellen gesättigt sind. Darüber hinaus stellte Bohr fest, dass ein steigender CO2-Druck diese Kurve nach rechts verschiebt – d. h. höhere CO2-Konzentrationen erschweren die Sauerstoffbindung für Hämoglobin. Dieses Phänomen ist zusammen mit der Beobachtung, dass die Affinität von Hämoglobin für Sauerstoff mit steigendem pH-Wert zunimmt, als Bohr-Effekt bekannt.

Ein Rezeptormolekül weist eine kooperative Bindung auf, wenn seine Bindung an den Liganden nichtlinear mit der Ligandenkonzentration skaliert. Die Kooperativität kann positiv sein (wenn die Bindung eines Ligandenmoleküls die scheinbare Affinität des Rezeptors erhöht und damit die Wahrscheinlichkeit der Bindung eines anderen Ligandenmoleküls erhöht) oder negativ (wenn die Bindung eines Ligandenmoleküls die Affinität verringert und damit die Bindung anderer Ligandenmoleküle weniger wahrscheinlich macht). Die “fraktionelle Belegung” Y ¯ {\displaystyle {\bar {Y}}

eines Rezeptors mit einem bestimmten Liganden ist definiert als die Anzahl der ligandengebundenen Bindungsstellen geteilt durch die Gesamtmenge der Ligandenbindungsstellen: Y ¯ = + = {\displaystyle {\bar {Y}}={\frac {}{+}}={\frac {}{}}}

Wenn Y ¯ = 0 {\displaystyle {\bar {Y}}=0}

, dann ist das Protein vollständig ungebunden, und wenn Y ¯ = 1 {\displaystyle {\bar {Y}}=1}

, so ist es vollständig gesättigt. Wenn die Darstellung von Y ¯ {\displaystyle {\bar {Y}}

im Gleichgewicht in Abhängigkeit von der Ligandenkonzentration eine sigmoidale Form hat, wie von Bohr für Hämoglobin beobachtet, deutet dies auf eine positive Kooperativität hin. Ist dies nicht der Fall, so kann aus dieser Darstellung allein keine Aussage über die Kooperativität getroffen werden.
Das Konzept der kooperativen Bindung gilt nur für Moleküle oder Komplexe mit mehr als einer Ligandenbindungsstelle. Wenn mehrere Ligandenbindungsstellen vorhanden sind, aber die Bindung eines Liganden an eine der Stellen die anderen nicht beeinflusst, wird der Rezeptor als nicht kooperativ bezeichnet. Die Kooperativität kann homotrop sein, wenn ein Ligand die Bindung von Liganden der gleichen Art beeinflusst, oder heterotrop, wenn er die Bindung anderer Arten von Liganden beeinflusst. Im Fall von Hämoglobin beobachtete Bohr eine homotrope positive Kooperativität (die Bindung von Sauerstoff erleichtert die Bindung von mehr Sauerstoff) und eine heterotrope negative Kooperativität (die Bindung von CO2 verringert die Fähigkeit von Hämoglobin, Sauerstoff zu binden.)
Im Laufe des 20. Jahrhunderts wurden verschiedene Konzepte entwickelt, um die Bindung eines Liganden an ein Protein mit mehr als einer Bindungsstelle und die in diesem Zusammenhang beobachteten kooperativen Effekte zu beschreiben.
Die Hill-GleichungEdit
Die erste Beschreibung der kooperativen Bindung an ein Protein mit mehreren Bindungsstellen wurde von A.V. Hill entwickelt. Ausgehend von Beobachtungen der Sauerstoffbindung an Hämoglobin und der Vorstellung, dass die Kooperativität durch die Aggregation von Hämoglobinmolekülen entsteht, von denen jedes ein Sauerstoffmolekül bindet, schlug Hill eine phänomenologische Gleichung vor, die seitdem nach ihm benannt ist:
Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\displaystyle {\bar {Y}}={\frac {K\cdot {}^{n}}{1+K\cdot {}^{n}}}={\frac {^{n}}{K^{*}+^{n}}}={\frac {^{n}}{K_{d}^{n}+^{n}}}}

wobei n {\displaystyle n}

der “Hill-Koeffizient” ist, {\displaystyle }

die Ligandenkonzentration, K {\displaystyle K}

eine scheinbare Assoziationskonstante (in der ursprünglichen Form der Gleichung verwendet), K ∗ {\displaystyle K^{*}}

ist eine empirische Dissoziationskonstante, und K d {\displaystyle K_{d}}

eine mikroskopische Dissoziationskonstante (wird in modernen Formen der Gleichung verwendet und entspricht einem E C 50 {\displaystyle \mathrm {EC} _{50}}

). Wenn n < 1 {\displaystyle n<1}

, weist das System eine negative Kooperativität auf, während die Kooperativität positiv ist, wenn n > 1 {\displaystyle n>1}

. Die Gesamtzahl der Ligandenbindungsstellen ist eine Obergrenze für n {\displaystyle n}

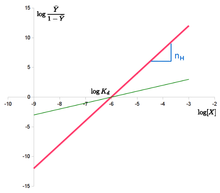
. Die Hill-Gleichung kann linearisiert werden als: log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}=n\cdot {}\log-n\cdot {}\log K_{d}}

Den “Hill-Plot” erhält man durch Auftragen von log Y ¯ 1 – Y ¯ {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}}

gegen log {\displaystyle \log}

. Im Fall der Hill-Gleichung handelt es sich um eine Linie mit der Steigung n H {\displaystyle n_{H}}

und Achsenabschnitt log ( K d ) {\displaystyle \log(K_{d})}

. Dies bedeutet, dass die Kooperativität als fest angenommen wird, d. h. sie ändert sich nicht mit der Sättigung. Es bedeutet auch, dass die Bindungsstellen immer die gleiche Affinität aufweisen und die Kooperativität nicht aus einer mit der Ligandenkonzentration steigenden Affinität resultiert.
Die Adair-GleichungEdit
G.S. Adair stellte fest, dass der Hill-Plot für Hämoglobin keine gerade Linie war, und stellte die Hypothese auf, dass die Bindungsaffinität kein fester Term ist, sondern von der Ligandensättigung abhängt. Nachdem er nachgewiesen hatte, dass Hämoglobin vier Häms (und damit Bindungsstellen für Sauerstoff) enthält, ging er von der Annahme aus, dass vollständig gesättigtes Hämoglobin in Stufen gebildet wird, mit Zwischenformen mit einem, zwei oder drei gebundenen Sauerstoffmolekülen. Die Bildung jeder Zwischenstufe aus ungebundenem Hämoglobin kann mit einer scheinbaren makroskopischen Assoziationskonstante K i {\displaystyle K_{i}} beschrieben werden

beschrieben werden. Die sich daraus ergebende fraktionierte Belegung kann ausgedrückt werden als: Y ¯ = 1 4 ⋅ K I + 2 K I I 2 + 3 K I I I 3 + 4 K I V 4 1 + K I + K I I 2 + K I I I 3 + K I V 4 {\displaystyle {\bar {Y}}={\frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, für jedes Protein mit n Ligandenbindungsstellen:
Y ¯ = 1 n K I + 2 K I I 2 + … + n K n n 1 + K I + K I I 2 + … + K n n {\displaystyle {\bar {Y}}={\frac {1}{n}}{\frac {K_{I}+2K_{II}^{2}+\ldots +nK_{n}^{n}}{1+K_{I}+K_{II}^{2}+\ldots +K_{n}^{n}}}}

wobei n die Anzahl der Bindungsstellen bezeichnet und jedes K i {\displaystyle K_{i}}

ist eine kombinierte Assoziationskonstante, die die Bindung von i Ligandenmolekülen beschreibt. Kombiniert man die Adair-Behandlung mit dem Hill-Plot, so erhält man die moderne experimentelle Definition der Kooperativität (Hill, 1985, Abeliovich, 2005). Der sich daraus ergebende Hill-Koeffizient, oder besser gesagt die Steigung des Hill-Plots, wie er sich aus der Adair-Gleichung errechnet, kann als das Verhältnis zwischen der Varianz der Bindungszahl und der Varianz der Bindungszahl in einem äquivalenten System von nicht interagierenden Bindungsstellen dargestellt werden. Somit definiert der Hill-Koeffizient die Kooperativität als eine statistische Abhängigkeit einer Bindungsstelle vom Zustand der anderen Stelle(n).
Die Klotz-GleichungBearbeiten
Im Zusammenhang mit kalziumbindenden Proteinen hat Irving Klotz die Adair’schen Assoziationskonstanten dekonvolutiert, indem er die schrittweise Bildung von Zwischenstufen berücksichtigte und versuchte, die kooperative Bindung in Form von Elementarprozessen auszudrücken, die durch das Massenwirkungsgesetz geregelt werden. In seinem Rahmen, K 1 {\displaystyle K_{1}}

die Assoziationskonstante für die Bindung des ersten Ligandenmoleküls, K 2 {\displaystyle K_{2}}

die Assoziationskonstante für die Bindung des zweiten Ligandenmoleküls (wenn das erste bereits gebunden ist) usw. Für Y ¯ {\displaystyle {\bar {Y}}

ergibt dies: Y ¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … K n ) n {\displaystyle {\bar {Y}}={\frac {1}{n}}{\frac {K_{1}+2K_{1}K_{2}^{2}+\ldots +n\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Es ist erwähnenswert, dass die Konstanten K 1 {\displaystyle K_{1}}

, K 2 {\displaystyle K_{2}}

und so weiter beziehen sich nicht auf einzelne Bindungsstellen. Sie beschreiben, wie viele Bindungsstellen besetzt sind, und nicht, welche. Diese Form hat den Vorteil, dass die Kooperativität bei der Betrachtung der Assoziationskonstanten leicht zu erkennen ist. Wenn alle Ligandenbindungsstellen mit einer mikroskopischen Assoziationskonstante K {\displaystyle K}

identisch sind, würde man erwarten, dass K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K {\displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}K,\ldots K_{n}={\frac {1}{n}}K}

(d.h. K i = n – i + 1 i K {\displaystyle K_{i}={\frac {n-i+1}{i}}K}

), wenn keine Kooperativität vorliegt. Wir haben positive Kooperativität, wenn K i {\displaystyle K_{i}}

über diesen erwarteten Werten für i > 1 {\displaystyle i>1} liegt

.
Die Klotz-Gleichung (die manchmal auch als Adair-Klotz-Gleichung bezeichnet wird) wird in der experimentellen Literatur immer noch häufig verwendet, um Messungen der Ligandenbindung in Form von aufeinanderfolgenden scheinbaren Bindungskonstanten zu beschreiben.
Pauling-GleichungBearbeiten
Ab Mitte des 20. Jahrhunderts gab es ein verstärktes Interesse an Modellen, die nicht nur die Bindungskurven phänomenologisch beschreiben, sondern auch einen zugrunde liegenden biochemischen Mechanismus bieten. Linus Pauling interpretierte die von Adair aufgestellte Gleichung neu und ging davon aus, dass seine Konstanten die Kombination aus der Bindungskonstante für den Liganden (K {\displaystyle K}

in der Gleichung unten) und der Energie aus der Wechselwirkung zwischen den Untereinheiten des kooperativen Proteins (α {\displaystyle \alpha }

unten) waren. Pauling leitete tatsächlich mehrere Gleichungen ab, je nach dem Grad der Wechselwirkung zwischen den Untereinheiten. Aufgrund falscher Annahmen über die Lokalisierung der Hämatome entschied er sich für die falsche Gleichung zur Beschreibung der Sauerstoffbindung durch Hämoglobin, wobei er davon ausging, dass die Untereinheiten in einem Quadrat angeordnet seien. Die folgende Gleichung liefert die Gleichung für eine tetraedrische Struktur, die im Fall von Hämoglobin genauer wäre: Y ¯ = K + 3 α K 2 2 + 3 α 3 K 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 + 4 α 3 K 3 3 + α 6 K 4 4 {\displaystyle {\bar {Y}}={\frac {K+3\alpha {}K^{2}^{2}+3\alpha {}^{3}K^{3}^{3}+\alpha {}^{6}K^{4}^{4}}}{1+4K+6\alpha {}K^{2}^{2}+4\alpha {}^{3}K^{3}^{3}+\alpha {}^{6}K^{4}^{4}}}}

Das KNF-ModellBearbeiten
Ausgehend von Ergebnissen, die zeigen, dass sich die Struktur kooperativer Proteine bei der Bindung an ihren Liganden verändert, Daniel Koshland und Kollegen verfeinerten die biochemische Erklärung des von Pauling beschriebenen Mechanismus. Das Koshland-Némethy-Filmer (KNF) Modell geht davon aus, dass jede Untereinheit in einer von zwei Konformationen vorliegen kann: aktiv oder inaktiv. Die Bindung eines Liganden an eine Untereinheit würde eine unmittelbare Konformationsänderung dieser Untereinheit von der inaktiven zur aktiven Konformation bewirken, ein Mechanismus, der als “induzierte Anpassung” beschrieben wird. Die Kooperativität entstünde nach dem KNF-Modell durch Wechselwirkungen zwischen den Untereinheiten, deren Stärke je nach den relativen Konformationen der beteiligten Untereinheiten variiert. Für eine tetraedrische Struktur (sie betrachteten auch lineare und quadratische Strukturen) schlugen sie die folgende Formel vor:
Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B ( K X K t ) 2 + 3 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {\displaystyle {\bar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Wobei K X {\displaystyle K_{X}}

die Assoziationskonstante für X ist, K t {\displaystyle K_{t}}

ist das Verhältnis der Zustände B und A in Abwesenheit des Liganden (“Übergang”), K A B {\displaystyle K_{AB}}

und K B B {\displaystyle K_{BB}}

sind die relativen Stabilitäten von Paaren benachbarter Untereinheiten im Vergleich zu einem Paar, bei dem sich beide Untereinheiten im A-Zustand befinden (Man beachte, dass im KNF-Papier eigentlich N s {\displaystyle N_{s}}

, die Anzahl der besetzten Stellen, die hier das 4-fache von Y ¯ {\displaystyle {\bar {Y}}}

).
Das MWC-ModellBearbeiten


Das Monod-Wyman-Changeux (MWC)-Modell für konzertierte allosterische Übergänge ging einen Schritt weiter, indem es die Kooperativität auf der Grundlage der Thermodynamik und dreidimensionaler Konformationen untersuchte. Es wurde ursprünglich für oligomere Proteine mit symmetrisch angeordneten, identischen Untereinheiten formuliert, von denen jede eine Ligandenbindungsstelle besitzt. Nach diesem Modell existieren zwei (oder mehr) ineinander überführbare Konformationszustände eines allosterischen Proteins in einem thermischen Gleichgewicht. Die Zustände – oft als angespannt (T) und entspannt (R) bezeichnet – unterscheiden sich in ihrer Affinität für das Ligandenmolekül. Das Verhältnis zwischen den beiden Zuständen wird durch die Bindung von Ligandenmolekülen reguliert, die den Zustand mit der höheren Affinität stabilisieren. Wichtig ist, dass alle Untereinheiten eines Moleküls gleichzeitig den Zustand wechseln, ein Phänomen, das als “konzertierter Übergang” bekannt ist.
Die allosterische Isomerisierungskonstante L beschreibt das Gleichgewicht zwischen beiden Zuständen, wenn kein Ligandenmolekül gebunden ist: L = {\displaystyle L={\frac {\left}{\left}}

. Wenn L sehr groß ist, befindet sich der größte Teil des Proteins in Abwesenheit des Liganden im T-Zustand. Wenn L klein ist (nahe bei eins), ist der R-Zustand fast genauso stark besiedelt wie der T-Zustand. Das Verhältnis der Dissoziationskonstanten für den Liganden aus dem T- und R-Zustand wird durch die Konstante c beschrieben: c = K d R K d T {\displaystyle c={\frac {K_{d}^{R}}{K_{d}^{T}}}}

. Wenn c = 1 {\displaystyle c=1}

, haben sowohl der R- als auch der T-Zustand die gleiche Affinität für den Liganden, und der Ligand beeinflusst die Isomerisierung nicht. Der Wert von c gibt auch an, wie stark sich das Gleichgewicht zwischen den T- und R-Zuständen nach der Bindung des Liganden ändert: Je kleiner c ist, desto mehr verschiebt sich das Gleichgewicht nach einer Bindung in Richtung des R-Zustands. Mit α = K d R {\displaystyle \alpha ={\frac {}{K_{d}^{R}}}}

, wird die fraktionierte Belegung beschrieben als: Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {Y}}={\frac {\alpha (1+\alpha )^{n-1}+Lc\alpha (1+c\alpha )^{n-1}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Der sigmoide Hill-Plot allosterischer Proteine kann dann als progressiver Übergang vom T-Zustand (niedrige Affinität) zum R-Zustand (hohe Affinität) mit zunehmender Sättigung analysiert werden. Die Steigung des Hill-Diagramms hängt ebenfalls von der Sättigung ab, mit einem Maximalwert am Knickpunkt. Die Schnittpunkte zwischen den beiden Asymptoten und der y-Achse ermöglichen die Bestimmung der Affinitäten der beiden Zustände für den Liganden.

In Proteinen sind Konformationsänderungen oft mit Aktivität oder Aktivität gegenüber bestimmten Zielen verbunden. Diese Aktivität ist oft das, was physiologisch relevant ist oder was experimentell gemessen wird. Der Grad der Konformationsänderung wird durch die Zustandsfunktion R ¯ {\displaystyle {\bar {R}} beschrieben}

, die den Anteil des Proteins im R {\displaystyle R}

state. Wie das Energiediagramm verdeutlicht, ist R ¯ {\displaystyle {\bar {R}}

steigt mit der Bindung weiterer Ligandenmoleküle. Der Ausdruck für R ¯ {\displaystyle {\bar {R}}

ist: R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {R}}={\frac {(1+\alpha )^{n}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Ein wesentlicher Aspekt des MWC-Modells ist, dass die Kurven für Y ¯ {\displaystyle {\bar {Y}}}

und R ¯ {\displaystyle {\bar {R}}

nicht übereinstimmen, d.h. die fraktionelle Sättigung ist kein direkter Indikator für den Konformationszustand (und damit für die Aktivität). Darüber hinaus können die Ausmaße der Kooperativität der Bindung und der Kooperativität der Aktivierung sehr unterschiedlich sein: Ein Extremfall ist der Motor der Geißel der Bakterien mit einem Hill-Koeffizienten von 1,7 für die Bindung und 10,3 für die Aktivierung. Die Supra-Linearität der Reaktion wird manchmal als Ultra-Sensitivität bezeichnet.
Bindet ein allosterisches Protein an ein Ziel, das ebenfalls eine höhere Affinität für den R-Zustand hat, so stabilisiert die Bindung des Ziels den R-Zustand weiter und erhöht damit die Ligandenaffinität. Bindet ein Target hingegen bevorzugt an den T-Zustand, so wirkt sich die Targetbindung negativ auf die Ligandenaffinität aus. Solche Targets werden als allosterische Modulatoren bezeichnet.
Seit seinen Anfängen wurde der MWC-Rahmen erweitert und verallgemeinert. Es wurden Variationen vorgeschlagen, um beispielsweise Proteine mit mehr als zwei Zuständen, Proteine, die an mehrere Arten von Liganden oder mehrere Arten von allosterischen Modulatoren binden, und Proteine mit nicht identischen Untereinheiten oder Ligandenbindungsstellen zu berücksichtigen.