Por Evan Ma

(tutor de Matemáticas y Física en el Centro de Aprendizaje The Edge)

La función logarítmica parece confundir a muchos alumnos que estudian el programa IB Math SL. Para entenderla bien, definamos

donde , un número real estrictamente positivo, se llama la base y es la potencia. Por ejemplo, todos nos sabemos de memoria lo siguiente:

y así sucesivamente. La función logarítmica lo hace al revés: dado un número como argumento, da la potencia sujeta a una base especificada, por lo que se define así.

Si

entonces

Por tanto, está claro que

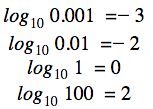
y así sucesivamente. Veamos otros ejemplos en los que intervienen otras bases:

Completemos las siguientes preguntas como práctica: (a) , (b) , (c) , (d) . Las respuestas se encuentran al final de este blog.

A partir de la definición de logaritmo, también podemos ver que si elevamos la base por la base-logaritmo de un número real , obtendremos de nuevo el número , viz

Puedes intentar comprobarlo utilizando tu calculadora para diferentes bases válidas. Esta identidad es importante cuando intentamos resolver ecuaciones logarítmicas, cuyos ejemplos se darán a continuación.

Ahora, echemos un vistazo a las reglas del logaritmo. De forma similar a la definición del logaritmo, utilizamos las leyes de los índices para derivar las reglas:

1. El logaritmo de un producto es la suma de los logaritmos

Prueba: Digamos y , por tanto

2. El logaritmo de base de Mr es por

Prueba: Di , por tanto

3. El logaritmo de un cociente es la diferencia de logaritmos

Prueba: Digamos que y , por tanto

4. La última regla se llama fórmula de cambio de base. Utilizaremos un ejemplo como herramienta para derivar la fórmula. Supongamos que queremos saber a qué potencia hay que elevar 2 para obtener 50. Como 50 no es una potencia entera de 2, la respuesta no es muy obvia. Por lo tanto, escribimos

y por lo tanto. Para encontrar , digamos que aplicamos el logaritmo de base 10 a ambos lados de la ecuación, ya que nuestra calculadora puede no tener la tecla de logaritmo de base 2:

Corregido a 4 cifras significativas, el valor de es aproximadamente 5,644. De hecho, puedes verificar tu respuesta elevando 2 a la potencia de 5,644 para ver que la respuesta es aproximadamente 50.

Para generalizar el problema, digamos que tenemos que encontrar tal que y el logaritmo de base- no está a nuestra disposición, por lo que podemos utilizar en su lugar el logaritmo de base- según la ecuación

y por tanto

A modo de ejemplo, consideremos lo siguiente. Supongamos que se deposita una cantidad de 10.000 dólares a un interés del 2,5% anual, compuesto anualmente. ¿Cuánto tiempo debe mantenerse el dinero en la cuenta para que crezca hasta los 50.000 dólares?

Para responder a la pregunta, básicamente estamos tratando de encontrar n tal que

Como mi simple calculadora científica no me permite especificar una base de 1.025 para la clave logarítmica, tendré que recurrir a la fórmula de cambio de base y utilizar la base-10, y por tanto

Como el interés se compone anualmente, tardará 66 años en crecer al menos 5 veces.

Habiendo explorado las reglas de los logaritmos, introducimos la función logarítmica natural, o . Es base-, donde es el eminente número irracional ≈2,71828 y cuya importancia en las ciencias y las matemáticas no se puede enfatizar lo suficiente. Por lo tanto, el logaritmo de base se define de la siguiente manera.

Si

entonces

A continuación, veamos dos ejemplos en los que se cometen errores comunes al resolver ecuaciones de logaritmos. A ver si eres capaz de identificar el error.

¿Dónde está el error? Fíjate bien. Por supuesto, en el segundo paso no se puede “dividir” el logaritmo a través del signo de suma. Recuerda que sólo puedes “dividir” un logaritmo en una suma si el logaritmo se aplica a un producto, no a una suma. Por lo tanto, los pasos correctos son los siguientes:

Ahora, veamos el siguiente ejemplo, y veamos si puedes identificar el error:

¿Dónde está el error? Sí, está en el segundo paso: un cociente de logaritmos no es, por supuesto, el logaritmo del cociente. Más bien, podemos utilizar la fórmula de cambio de base para simplificar el primer paso, de la siguiente manera:

Por último, ilustraremos cómo utilizar las reglas del logaritmo para resolver lo siguiente:

Podrás observar que la incógnita aparece como base y como variable en el argumento del logaritmo. ¿Cómo podemos resolver ? El método sigue dependiendo de aplicar las reglas del logaritmo de forma coherente. En primer lugar, elevamos ambos lados como potencias de la base , y por lo tanto

Podrás recordar de la definición de logaritmo que el lado izquierdo se acaba de convertir en el argumento del logaritmo, y por tanto

Reorganizando la ecuación anterior, tenemos que resolver

Notando que esto se parece a una cuadrática en , resolvemos para de la siguiente manera:

Ahora, ¿dónde está la raíz negativa? Como es también la base del logaritmo, la raíz negativa se rechaza como solución. Por lo tanto, es la respuesta final.

Al repasar los ejemplos anteriores, puedes ver que resolver una ecuación logarítmica aparentemente difícil no es nada difícil – simplemente aplica las reglas del logaritmo de forma coherente y se puede obtener la solución correcta.

Respuestas a las preguntas: (a) 2 (b) 3 (c) -3 (d) -2.