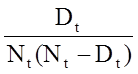Hay varias formas diferentes de estimar una función de supervivencia o una curva de supervivencia. Hay una serie de métodos paramétricos populares que se utilizan para modelar los datos de supervivencia, y difieren en términos de las suposiciones que se hacen sobre la distribución de los tiempos de supervivencia en la población. Algunas de las distribuciones más populares son la exponencial, la de Weibull, la de Gompertz y la log-normal.2 Quizá la más popular sea la distribución exponencial, que asume que la probabilidad de que un participante sufra el suceso de interés es independiente del tiempo que lleve sin sufrirlo. Otras distribuciones hacen diferentes suposiciones sobre la probabilidad de que un individuo desarrolle un evento (es decir, puede aumentar, disminuir o cambiar con el tiempo). Se pueden encontrar más detalles sobre los métodos paramétricos para el análisis de supervivencia en Hosmer y Lemeshow y Lee y Wang1,3.

Nos centramos aquí en dos métodos no paramétricos, que no hacen suposiciones sobre cómo cambia la probabilidad de que una persona desarrolle el evento con el tiempo. Con los métodos no paramétricos, estimamos y trazamos la distribución de la supervivencia o la curva de supervivencia. Las curvas de supervivencia suelen representarse como funciones escalonadas, como se muestra en la siguiente figura. El tiempo se muestra en el eje X y la supervivencia (proporción de personas en riesgo) se muestra en el eje Y. Obsérvese que el porcentaje de participantes que sobreviven no siempre representa el porcentaje que está vivo (lo que supone que el resultado de interés es la muerte). “Supervivencia” también puede referirse a la proporción que está libre de otro evento de resultado (por ejemplo, porcentaje libre de IM o enfermedad cardiovascular), o también puede representar el porcentaje que no experimenta un resultado saludable (por ejemplo, remisión del cáncer).

Función de supervivencia

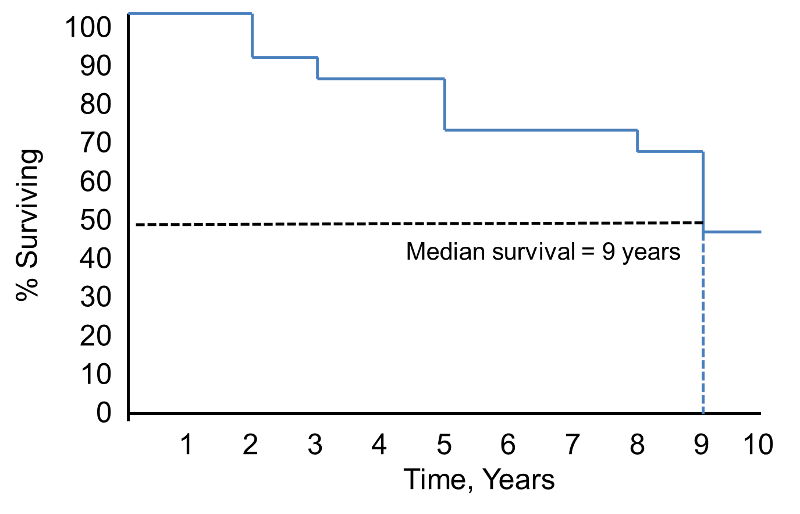
Nótese que la probabilidad de supervivencia es del 100% durante 2 años y luego baja al 90%. La mediana de supervivencia es de 9 años (es decir, el 50% de la población sobrevive 9 años; véanse las líneas discontinuas).

Ejemplo:

Considérese una pequeña cohorte prospectiva diseñada para estudiar el tiempo hasta la muerte. En el estudio participan 20 personas de 65 años o más; se inscriben durante un período de 5 años y se les hace un seguimiento de hasta 24 años hasta que mueren, el estudio termina o abandonan el estudio (pérdida de seguimiento). Los datos se muestran a continuación. En el estudio, hay 6 muertes y 3 participantes con seguimiento completo (es decir, 24 años). Los 11 restantes tienen menos de 24 años de seguimiento debido a que se inscribieron tarde o perdieron el seguimiento.

Número de identificación del participante	Año de la muerte	Año de último contacto
1		24
2	3
3		11
4		19
5		24
6		13
7	14
8		2
9		18
10		17
11		24
12		21
13		12
14	1
15		10
16	23
17		6
18	5
19		9
20	17

Tabla de vida (Tabla Actuarial)

Una forma de resumir las experiencias de los participantes es con una tabla de vida, o una tabla actuarial. Las tablas de vida se utilizan a menudo en el sector de los seguros para estimar la esperanza de vida y fijar las primas. Nos centramos en un tipo particular de tabla de vida que se utiliza ampliamente en el análisis bioestadístico, denominada tabla de vida de cohortes o tabla de vida de seguimiento. La tabla de vida de seguimiento resume las experiencias de los participantes durante un periodo de seguimiento predefinido en un estudio de cohortes o en un ensayo clínico hasta el momento del evento de interés o el final del estudio, lo que ocurra primero.

Para construir una tabla de vida, primero organizamos los tiempos de seguimiento en intervalos igualmente espaciados. En la tabla anterior tenemos un seguimiento máximo de 24 años, y consideramos intervalos de 5 años (0-4, 5-9, 10-14, 15-19 y 20-24 años). Sumamos el número de participantes que están vivos al principio de cada intervalo, el número que muere y el número que se censura en cada intervalo.

Intervalo en años	Número de vivos al comienzo del intervalo	Número de muertes durante el intervalo	Número censurado
0-4	20	2	1
5-9	17	1	2
10-14	14	1	4
15-19	9	1	3
20-24	5	1	4

Utilizamos la siguiente notación en nuestro análisis de la tabla de vida. Primero definimos la notación y luego la utilizamos para construir la tabla de vida.

• Nt = número de participantes que están libres de eventos y se consideran en riesgo durante el intervalo t (por ejemplo, en este ejemplo el número vivo ya que nuestro resultado de interés es la muerte)
• Dt = número de participantes que mueren (o sufren el evento de interés) durante el intervalo t
• Ct = número de participantes que son censurados durante el intervalo t Nt* = el número medio de participantes en riesgo durante el intervalo t
• Nt* = el número medio de participantes en riesgo durante el intervalo t [Al construir tablas de vida actuariales, se suelen hacer las siguientes suposiciones: En primer lugar, se supone que los sucesos de interés (por ejemplo, las muertes) se producen al final del intervalo y que los sucesos censurados se producen de manera uniforme (o pareja) a lo largo del intervalo. Por lo tanto, a menudo se realiza un ajuste en Nt para reflejar el número medio de participantes en riesgo durante el intervalo, Nt*, que se calcula como sigue Nt* =Nt-Ct/2 (es decir, restamos la mitad de los eventos censurados).
• qt = proporción que muere (o sufre un evento) durante el intervalo t, qt = Dt/Nt*
• pt = proporción que sobrevive (permanece libre de eventos) al intervalo t, pt = 1-qt
• St, la proporción que sobrevive (o permanece libre de eventos) más allá del intervalo t; a veces se denomina probabilidad de supervivencia acumulada y se calcula como sigue: En primer lugar, la proporción de participantes que sobreviven más allá del momento 0 (el momento de inicio) se define como S0 = 1 (todos los participantes vivos o libres de eventos en el momento cero o de inicio del estudio). La proporción que sobrevive a cada intervalo subsiguiente se calcula utilizando los principios de la probabilidad condicional introducidos en el módulo de Probabilidad. En concreto, la probabilidad de que un participante sobreviva al intervalo 1 es S1 = p1. La probabilidad de que un participante sobreviva al intervalo 2 significa que ha tenido que sobrevivir al intervalo 1 y al intervalo 2: S2 = P(sobrevivir al intervalo 2) = P(sobrevivir al intervalo 2)*P(sobrevivir al intervalo 1), o S2 = p2*S1. En general, St+1 = pt+1*St.

El formato de la tabla de seguimiento de la vida se muestra a continuación.

Para el primer intervalo, de 0 a 4 años: En el momento 0, el inicio del primer intervalo (0-4 años), hay 20 participantes vivos o en riesgo. Dos participantes mueren en el intervalo y 1 es censurado. Aplicamos la corrección por el número de participantes censurados durante ese intervalo para producir Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. Los cálculos de las restantes columnas se muestran en la tabla. La probabilidad de que un participante sobreviva más allá de 4 años, o más allá del primer intervalo (utilizando el límite superior del intervalo para definir el tiempo) es S4 = p4 = 0,897.

Para el segundo intervalo, de 5 a 9 años: El número en riesgo es el número en riesgo en el intervalo anterior (0-4 años) menos los que mueren y son censurados (es decir, Nt = Nt-1-Dt-1-Ct-1 = 20-2-1 = 17). La probabilidad de que un participante sobreviva más allá de los 9 años es S9 = p9*S4 = 0,937*0,897 = 0,840.

Intervalo en años	Número en riesgo durante el intervalo, Nt	Número medio en riesgo durante el intervalo, Nt*	Número de muertes durante el intervalo, Dt	Pérdida de seguimiento, Ct	Proporción que muere Durante el intervalo, qt	Entre los que están en riesgo, proporción que sobrevive Intervalo, pt	Probabilidad de supervivencia St
0-4	20	20-(1/2) = 19.5	2	1	2/19.5 = 0.103	1-0.103 = 0.897	1(0.897) = 0.897
5-9	17	17-(2/2) = 16.0	1	2	1/16 = 0.063	1-0.063 = 0.937	(0,897)(0,937)=0,840

La tabla de vida de seguimiento completa se muestra a continuación.

Intervalo en años	Número en riesgo durante el intervalo, Nt	Número medio en riesgo durante el intervalo, Nt*	Número de muertes durante el intervalo, Dt	Pérdida de seguimiento, Ct	Proporción que muere Durante el intervalo, qt	Entre los de riesgo, Proporción que sobrevive Intervalo, pt	Probabilidad de supervivencia St
0-4	20	19.5	2	1	0.103	0.897	0.897
5-9	17	16.0	1	2	0.063	0.937	0.840
10-14	14	12.0	1	4	0.083	0.917	0.770
15-19	9	7.5	1	3	0.133	0.867	0.668
20-24	5	3.0	1	4	0.333	0,667	0,446

Esta tabla utiliza el método actuarial para construir la tabla de seguimiento de la vida en la que el tiempo se divide en intervalos igualmente espaciados.

Enfoque de Kaplan-Meier (límite del producto)

Un problema con el enfoque de la tabla de vida mostrado anteriormente es que las probabilidades de supervivencia pueden cambiar dependiendo de cómo se organicen los intervalos, particularmente con muestras pequeñas. El enfoque de Kaplan-Meier, también llamado enfoque de límite de producto, es un enfoque popular que aborda este problema mediante la reestimación de la probabilidad de supervivencia cada vez que ocurre un evento.

El uso apropiado del enfoque de Kaplan-Meier se basa en la suposición de que la censura es independiente de la probabilidad de desarrollar el evento de interés y que las probabilidades de supervivencia son comparables en los participantes que se reclutan al principio y al final del estudio. Cuando se comparan varios grupos, también es importante que estos supuestos se cumplan en cada grupo de comparación y que, por ejemplo, la censura no sea más probable en un grupo que en otro.

La tabla siguiente utiliza el enfoque de Kaplan-Meier para presentar los mismos datos que se presentaron anteriormente utilizando el enfoque de tabla de vida. Obsérvese que comenzamos la tabla con Tiempo=0 y Probabilidad de Supervivencia = 1. En el Tiempo=0 (línea de base, o inicio del estudio), todos los participantes están en riesgo y la probabilidad de supervivencia es 1 (o 100%). Con el enfoque de Kaplan-Meier, la probabilidad de supervivencia se calcula utilizando St+1 = St*((Nt+1-Dt+1)/Nt+1). Obsérvese que los cálculos realizados con el enfoque de Kaplan-Meier son similares a los realizados con el enfoque de la tabla de vida actuarial. La principal diferencia son los intervalos de tiempo, es decir, con el enfoque de la tabla de vida actuarial consideramos intervalos igualmente espaciados, mientras que con el enfoque de Kaplan-Meier, utilizamos los tiempos de los eventos observados y los tiempos de censura. Los cálculos de las probabilidades de supervivencia se detallan en las primeras filas de la tabla.

Tabla de vida utilizando el enfoque de Kaplan-Meier

Tiempo, Años	Número en riesgo Nt	Número de muertes Dt	Número de censurados Ct	Probabilidad de supervivencia St+1 = St*((Nt+1-Dt+1)/Nt+1)
0	20		1
1	20	1		1*((20-1)/20) = 0.950
2	19		1	0.950*((19-0)/19)=0.950
3	18	1		0.950*((18-1)/18) = 0.897
5	17	1		0.897*((17-1)/17) = 0.844
6	16		1	0.844
9	15		1	0.844
10	14		1	0.844
11	13		1	0.844
12	12		1	0.844
13	11		1	0.844
14	10	1		0.760
17	9	1	1	0.676
18	7		1	0.676
19	6		1	0.676
21	5		1	0.676
23	4	1		0.507
24	3		3	0,507

Con grandes conjuntos de datos, estos cálculos son tediosos. Sin embargo, estos análisis pueden ser generados por programas de computación estadística como SAS. También se puede utilizar Excel para calcular las probabilidades de supervivencia una vez que los datos se organizan por tiempos y se resumen los números de eventos y los tiempos censurados.

A partir de la tabla de vida podemos producir una curva de supervivencia de Kaplan-Meier.

Curva de supervivencia de Kaplan-Meier para los datos anteriores

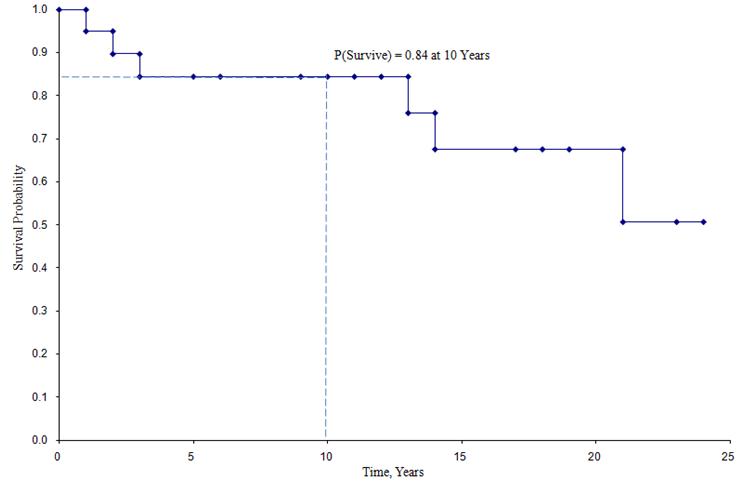
En la curva de supervivencia mostrada arriba, los símbolos representan cada tiempo de evento, ya sea una muerte o un tiempo censurado. A partir de la curva de supervivencia, también podemos estimar la probabilidad de que un participante sobreviva más allá de los 10 años situando los 10 años en el eje X y leyendo hacia arriba y hacia el eje Y. La proporción de participantes que sobreviven más allá de los 10 años es del 84%, y la proporción de participantes que sobreviven más allá de los 20 años es del 68%. La mediana de supervivencia se estima situando 0,5 en el eje Y y leyendo por encima y por debajo del eje X. La mediana de supervivencia es de aproximadamente 23 años.

Errores estándar y estimaciones del intervalo de confianza de las probabilidades de supervivencia

Estas estimaciones de las probabilidades de supervivencia en momentos específicos y la mediana del tiempo de supervivencia son estimaciones puntuales y deben interpretarse como tales. Existen fórmulas para producir errores estándar y estimaciones de intervalos de confianza de las probabilidades de supervivencia que pueden generarse con muchos paquetes informáticos estadísticos. Una fórmula popular para estimar el error estándar de las estimaciones de supervivencia se llama fórmula de Greenwoods5 y es la siguiente:

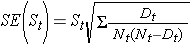
La cantidad 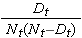se suma para los números en riesgo (Nt) y los números de muertes (Dt) que ocurren a través del tiempo de interés (es decir, acumulativo, a través de todos los tiempos antes del tiempo de interés, véase el ejemplo en la tabla siguiente). Los errores estándar se calculan para las estimaciones de supervivencia de los datos de la tabla siguiente. Obsérvese que la última columna muestra la cantidad 1,96*SE(St), que es el margen de error y se utiliza para calcular las estimaciones del intervalo de confianza del 95% (es decir, St ± 1,96 x SE(St)).

Errores estándar de las estimaciones de supervivencia

Tiempo, Años	Número en riesgo Nt	Número de muertes Dt	Supervivencia Probabilidad St				1.96*SE (St)
0	20		1		.
1	20	1	0.950	0.003	0.003	0.049	0.096
2	19		0.950	0.000	0.003	0.049	0.096
3	18	1	0.897	0.003	0.006	0.069	0.135
5	17	1	0.844	0.004	0.010	0.083	0.162
6	16		0.844	0.000	0.010	0.083	0.162
9	15		0.844	0.000	0.010	0.083	0.162
10	14		0.844	0.000	0.010	0.083	0.162
11	13		0.844	0.000	0.010	0.083	0.162
12	12		0.844	0.000	0.010	0.083	0.162
13	11		0.844	0.000	0.010	0.083	0.162
14	10	1	0.760	0.011	0.021	0.109	0.214
17	9	1	0.676	0.014	0.035	0.126	0.246
18	7		0.676	0.000	0.035	0.126	0.246
19	6		0.676	0.000	0.035	0.126	0.246
21	5		0.676	0.000	0.035	0.126	0.246
23	4	1	0.507	0.083	0.118	0.174	0.341
24	3		0.507	0,000	0,118	0,174	0,341

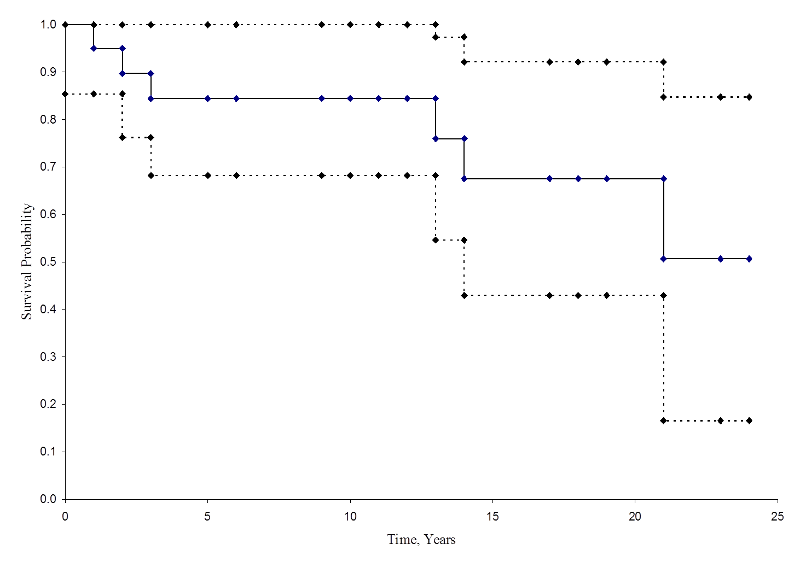
La figura siguiente resume las estimaciones y los intervalos de confianza en la figura siguiente. La curva de supervivencia de Kaplan-Meier se muestra como una línea sólida, y los límites de confianza del 95% se muestran como líneas punteadas.

Curva de supervivencia de Kaplan-Meier con intervalos de confianza

Curvas de incidencia acumulada

Algunos investigadores prefieren generar curvas de incidencia acumulada, en contraposición a las curvas de supervivencia que muestran las probabilidades acumuladas de experimentar el evento de interés. La incidencia acumulada, o la probabilidad de fracaso acumulada, se calcula como 1-St y puede calcularse fácilmente a partir de la tabla de vida utilizando el enfoque de Kaplan-Meier. Las probabilidades de fallo acumuladas para el ejemplo anterior se muestran en la siguiente tabla.

Tabla de vida con probabilidades de fallo acumuladas

Tiempo, Años	Número de Riesgos Nt	Número de Muertes Dt	Número Censurado Ct	Probabilidad de supervivencia St	Probabilidad de fracaso 1-St
0	20		1	0
1	20	1		0.950	0.050
2	19		1	0.950	0.050
3	18	1		0.897	0.103
5	17	1		0.844	0.156
6	16		1	0.844	0.156
9	15		1	0.844	0.156
10	14		1	0.844	0.156
11	13		1	0.844	0.156
12	12		1	0.844	0.156
13	11		1	0.844	0.156
14	10	1		0.760	0.240
17	9	1	1	0.676	0.324
18	7		1	0.676	0.324
19	6		1	0.676	0.324
21	5		1	0.676	0.324
23	4	1		0.507	0.493
24	3		3	0.507	0,493

La siguiente figura muestra la incidencia acumulada de muerte de los participantes inscritos en el estudio descrito anteriormente.

Curva de incidencia acumulada

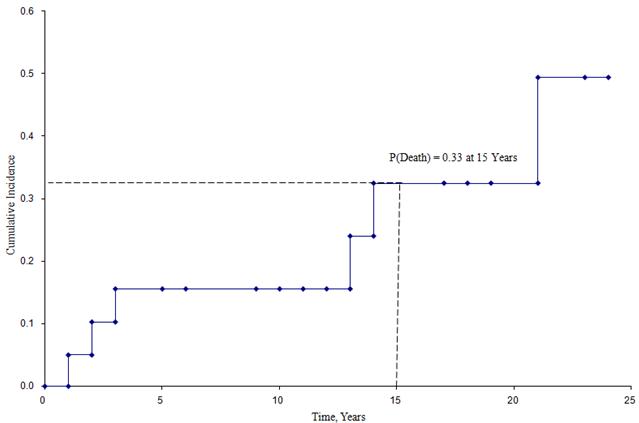
A partir de esta figura podemos estimar la probabilidad de que un participante muera en un momento determinado. Por ejemplo, la probabilidad de muerte es de aproximadamente un 33% a los 15 años (ver líneas discontinuas).

Volver al principio | página anterior | página siguiente