Aristoteles (Ἀριστοτέλης) 384-322 eaa. oli kreikkalainen filosofi ja tiedemies, joka syntyi Stagiran kaupungissa klassisessa Kreikassa.

17-vuotiaana hän liittyi Platonin akatemiaan Ateenassa ja pysyi siellä kolmekymmentäseitsemänvuotiaaksi (n. 347 eaa.)

Hänen kirjoituksensa kattavat monia aihepiirejä – muun muassa fysiikkaa, biologiaa, eläintietoa, logiikkaa, etiikkaa, runoutta, teatteria, musiikkia, kielitieteiden tutkimusta ja politiikkaa. Ne muodostavat länsimaisen filosofian ensimmäisen kattavan järjestelmän.

• Luettu ja muokattu Aristoteleelta. (2016, 20. lokakuuta). Wikipedia, The Free Encyclopedia.

Aristoteles esitti 3 liikkeen lakia, jotka perustuvat havaintoihin (mutta eivät kokeisiin)

* taivaalla (taivaankehässä) olevat kappaleet liikkuvat ympyräliikkeessä,ilman mitään ulkoista voimaa, joka pakottaisi ne tekemään niin.Maan päällä (maanpäällinen sfääri) olevat esineet liikkuvat suoraviivaisesti,ellei niitä pakoteta liikkumaan ympyräliikkeeseen.

Miten on työntämisen ja vetämisen laita?

Luonnonmukainen vs. epäluonnonmukainen liike

Mitä tapahtuisi, jos tykki ampuisi tykinkuulan? Aristoteles oletti, että se liikkuisi suoraviivaisesti (epäluonnollisen voiman takia) ja putoaisi sitten suoraan alas (toisen, luonnollisen voiman takia.)

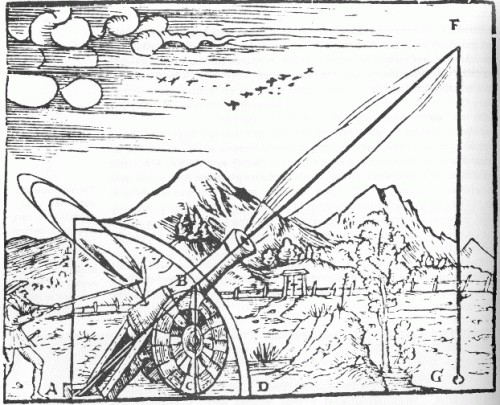
Aristoteleen mielestä, kun “väkivaltainen liike” (ihmisistä) on sammunut, luonnollinen liike ottaa vallan, ja silloin tykin kuula putoaa luonnolliseen paikkaansa, maahan.

Mutta kuten Galielo osoitti 1500-luvulla, Aristoteleen näkemys ei ole lainkaan oikea. Kuka tahansa, joka katsoo jousiampujaa ampumassa nuolta ilmaan ja tarkkailee tarkkaan, huomaa, että näin ei tapahdu.

Pystysuora liike vähenee hitaasti, saavuttaa nollan (huipussaan) ja kasvaa sitten päinvastaiseen (alaspäin) suuntaan.

Taivaalliset voimat vs. maanpäälliset voimat

Maa-asemassa olevilla esineillä (maanpäällisillä objekteilla) uskottiin olevan omat erilliset liikkeen lait. Maanpäällisten esineiden oletettiin aina pysähtyvän liikkumaan, itsestään, itsestään.

* esineet liikkuvat luonnostaan vain suoraviivaisesti.* Jotta esineet voisivat liikkua ympyränmuotoisesti, tarvitaan jokin ulkoinen voima,joka pitää ne vetäytyneinä ympyränmuotoiselle radalle

Ei Aristoteles myöskään koskaan suorittanut kokeita, joten hän oli hyvin rajoittunut siinä, mitä hän pystyi havaitsemaan.Keskiajalla Galilei (ja muut) tekivät kontrolloituja kokeita.Näiden kokeiden tuloksia analysoitiin matematiikan avulla.

Galileo oppi kriittisen ajattelun taidot isältään Vincenzolta

a. Kun pallo rullaa alaspäin, se liikkuu Maan painovoiman mukana ja sen nopeus kasvaa.

c. Kun pallo rullaa tasaisella tasolla, se ei liiku painovoiman mukana eikä sitä vastaan.

b. Kun nousukulma pienenee,pallo rullaa suuremman matkan ennen kuin se saavuttaa alkuperäisen korkeutensa.

Galileon johtopäätöstä tuki toinenkin päättelylinja.

Inclined Plane – Galileo’s Battle for the Heavens PBS NOVA

Rullaa palloja, sylintereitä ja putkia pitkin kaltevaa tasoa: Moment of Inertia

Erikoista: Brachistochrone – nopeimman laskeutumisen käyrä. Ja tautochrone- käyrä, jonka kohdalla aika, jonka ilman kitkaa tasaisessa painovoimassa alimpaan pisteeseensä liukuva kappale kuluttaa lähtöpisteestään riippumatta.

Aristotelesin liikelait.

Ote professori Michael Fowlerin luennosta, U. Va. Physics, 9/3/2008

http://galileoandeinstein.physics.virginia.edu/lectures/aristot2.html

Mitä Aristoteles saavutti noina vuosina Ateenassa, oli se, että hän aloitti järjestäytyneen tieteellisen tutkimuksen koulukunnan, jonka mittakaava ylitti huomattavasti kaiken aikaisemman. Hän määritteli ensin selvästi, mitä oli tieteellinen tieto ja miksi sitä olisi etsittävä. Toisin sanoen hän yksin keksi tieteen sellaisena kollektiivisena ja organisoituna yrityksenä, jollainen se nykyään on. Platonin akatemiassa oli yliopiston matematiikan laitosta vastaava laitos, Aristoteleella oli ensimmäinen luonnontieteiden laitos, joka oli todella erinomainen biologiassa mutta, kuten tulemme näkemään, hieman heikko fysiikassa.

Aristoteleen jälkeen ei ollut vastaavaa ammattimaista tiedeyritystä yli 2 000 vuoteen, ja hänen työnsä oli niin laadukasta, että kaikki hyväksyivät sen, ja se oli jo pitkään ollut osa kristillisen kirkon virallista ortodoksiaa 2 000 vuotta myöhemmin. Tämä oli valitettavaa, sillä kun Galilei kyseenalaisti joitakin yksinkertaista fysiikkaa koskevia väitteitä, hän joutui nopeasti vakaviin vaikeuksiin kirkon kanssa.
Aristotelesin tutkimusmenetelmä:

määrittelee aiheen

harkitsee aiheeseen liittyviä vaikeuksia tarkastelemalla yleisesti hyväksyttyjä näkemyksiä aiheesta ja aikaisempien kirjoittajien ehdotuksia

esittää omat argumenttinsa ja ratkaisunsa

Tätä mallia noudattavat nykyaikaiset tutkimuspaperit, Aristoteles määritteli tieteellisen tutkimuksen tavanomaisen ammattimaisen lähestymistavan.

Aristoteles kumosi usein vastakkaisen argumentin osoittamalla, että se johti absurdiin johtopäätökseen, tätä kutsutaan reductio ad absurdum (jonkin asian redusoiminen absurdiksi). Kuten tulemme myöhemmin näkemään, Galilei käytti juuri tällaista argumenttia itse Aristoteleen vastaista väitettä vastaan, 2 000 vuotta Aristoteleen jälkeen olevien aristoteelisten suureksi harmiksi.

Toisin kuin Platon, joka piti ainoana arvokkaana tieteenä abstraktien muotojen tarkastelua, Aristoteles harrasti kasvien ja eläinten yksityiskohtaista havainnointia ja paloittelua yrittäessään ymmärtää, miten kukin niistä sopi luonnon suureen järjestelmään ja mikä merkitys eläinten eri elimillä oli.

On olennaista tajuta, että Aristoteleen ympärillään jokapäiväisessä arjessa näkemä maailma oli todellakin hyvin erilainen kuin se, jonka näemme nykyään. Jokainen nykylapsi on syntymästään lähtien nähnyt autoja ja lentokoneita liikkumassa ja huomaa pian, että nämä asiat eivät ole eläviä, kuten ihmiset ja eläimet. Sitä vastoin suurin osa neljännen vuosisadan Kreikassa nähdystä liikkeestä oli ihmisiä, eläimiä ja lintuja, jotka kaikki olivat hyvin eläviä. Tällä kaikella liikkeellä oli tarkoitus, eläin liikkui jostain syystä johonkin paikkaan, jossa se mieluummin olisi, joten liikettä ohjasi eläimen tahto.

Aristoteleelle tämä liike siis täytti eläimen “luonteen”, aivan kuten sen luonnollinen kasvu täytti eläimen luonteen.

Selvittääkseen sellaisten asioiden liikkeen, jotka eivät selvästikään ole eläviä, kuten kädestä pudotetun kiven, Aristoteles laajensi jonkin asian “luonteen” käsitteen koskemaan myös elottoman aineen. Hän ehdotti, että tällaisten elottomien esineiden liike voitaisiin ymmärtää postuloimalla, että alkuaineet pyrkivät etsimään luonnollista paikkaansa asioiden järjestyksessä:

Siten maa liikkuu voimakkaimmin alaspäin,
myös vesi virtaa alaspäin, mutta ei niin voimakkaasti, sillä kivi putoaa veden läpi.
Ilma sitä vastoin liikkuu ylöspäin (kuplat vedessä),
ja tuli liikkuu kaikista voimakkaimmin ylöspäin, koska se ampuu ylöspäin ilman läpi.

Tätä yleistä teoriaa alkuaineiden liikkeistä on tietenkin tarkennettava, kun sitä sovelletaan todellisiin materiaaleihin, jotka ovat alkuaineiden sekoituksia. Hän päättelisi, että puussa on sekä maata että ilmaa, koska se ei uppoa veteen.

Luonnollinen liike ja väkivaltainen liike

Tavarat liikkuvat myös siksi, että niitä työnnetään. Jos kivi jätetään yksin ja ilman tukea, sen luonnollinen taipumus on pudota, mutta me voimme nostaa sitä tai jopa heittää sen ilmaan.

Aristoteles kutsui tällaista pakotettua liikettä “väkivaltaiseksi” liikkeeksi luonnollisen liikkeen vastakohtana.

Käsite “väkivaltainen” tarkoittaa vain sitä, että siihen kohdistetaan jokin ulkoinen voima.

Aristoteles ajatteli ensimmäisinä kvantitatiivisesti näissä liikkeissä esiintyviä nopeuksia. Hän esitti kaksi kvantitatiivista väitettä siitä, miten asiat putoavat (luonnollinen liike):

Painavammat asiat putoavat nopeammin, nopeus on verrannollinen painoon.

Tämän tietyn kappaleen putoamisnopeus riippuu kääntäen sen väliaineen tiheydestä, jonka läpi se putoaa.

Siten esimerkiksi sama kappale putoaa kaksi kertaa nopeammin väliaineen läpi, jonka tiheys on puolet pienempi.

Huomattakoon, että näissä säännöissä on tiettyä eleganssia, houkuttelevaa kvantitatiivista yksinkertaisuutta. Ja jos pudotat kiven ja paperinpalasen, on selvää, että painavampi kappale todellakin putoaa nopeammin, ja veden läpi putoava kivi varmasti hidastuu veden takia, joten säännöt vaikuttavat aluksi uskottavilta.

Yllättävää on, että ottaen huomioon Aristoteleen huolelliset havainnot niin monista asioista, hän ei tarkistanut näitä sääntöjä millään vakavalla tavalla.

Ei olisi kestänyt kauaa selvittää, jos esimerkiksi puolikas tiili putoaa puolet nopeammin kuin kokonainen tiili. Ilmeisesti hän ei pitänyt tätä tärkeänä.

Yllä olevasta toisesta väittämästä hän päätteli, että tyhjiötä ei voi olla olemassa, koska jos olisi, koska sen tiheys on nolla, kaikki kappaleet putoaisivat sen läpi äärettömällä nopeudella, mikä on selvästikin hölynpölyä.

Väkivaltaisen liikkeen osalta Aristoteles totesi, että liikkuvan kappaleen nopeus on suoraan verrannollinen kohdistettuun voimaan.

Tämä tarkoittaa ensinnäkin sitä, että jos lopetat työntämisen, kappale pysähtyy.

Tämä kuulostaa toki järkevältä säännöltä vaikkapa
työntäessä kirjalaatikkoa maton yli tai härkää, joka vetää auraa pellon halki.

(Tämä intuitiivisesti miellyttävä kuva ei kuitenkaan ota huomioon
laatikon ja maton välistä suurta kitkavoimaa.
Jos laittaisit laatikon kelkkaan ja työntäisit sitä jään poikki,
se ei pysähtyisi, kun lopettaisit työntämisen.
Satoja vuosia myöhemmin Galilei oivalsi kitkan merkityksen näissä tilanteissa.)

Oppimisstandardit

2016 Massachusettsin luonnontieteiden ja tekniikan/tekniikan opetussuunnitelman viitekehys
HS-PS2-1. Analysoi tietoja tukeaksesi väitettä, jonka mukaan Newtonin toinen liikelaki on
matemaattinen malli, joka kuvaa kappaleiden liikkeen muutosta (kiihtyvyyttä), kun
niihin vaikuttaa nettovoima.

HS-PS2-10(MA). Käytä vapaan kappaleen voimadiagrammeja, algebrallisia lausekkeita ja Newtonin liikelakeja ennustaaksesi nopeuden ja kiihtyvyyden muutoksia yhdessä ulottuvuudessa liikkuvalle kappaleelle eri tilanteissa

Massachusettsin historian ja yhteiskuntaopin opetussuunnitelman viitekehys

Länsimaisen sivilisaation juuret: Antiikin Kreikka, noin 800-300 eKr.
7.34 Kuvaile kreikkalaisten instituutioiden, kuten lyseon, voimistelukoulun ja Aleksandrian kirjaston, tarkoituksia ja kehitystehtäviä ja tunnista antiikin kreikkalaisten tärkeimmät saavutukset.

WHI.33 Tee yhteenveto siitä, miten tieteellinen vallankumous ja tieteellinen menetelmä johtivat uusiin teorioihin maailmankaikkeudesta, ja kuvaile tieteellisen vallankumouksen johtohahmojen, kuten Baconin, Kopernikuksen, Descartesin, Galilein, Keplerin ja
Newtonin saavutuksia.

A FRAMEWORK FOR K-12 SCIENCE EDUCATION: Practices, Crosscutting Concepts, and Core Ideas
PS2.A: FORCES AND MOTION
Miten voidaan ennustaa esineen jatkuvaa liikettä, liikkeen muutoksia tai vakautta?

Kappaleen ja toisen kappaleen vuorovaikutusta voidaan selittää ja ennustaa voimien käsitteen avulla, jotka voivat aiheuttaa muutoksen toisen tai molempien vuorovaikutuksessa olevien kappaleiden liikkeessä… Makrotasolla voimien vaikutuksen alaisen kappaleen liikettä säätelee Newtonin toinen laki… Kappaleiden välisten voimien ymmärtäminen on tärkeää, kun halutaan kuvata, miten kappaleiden liike muuttuu, sekä ennustaa systeemien stabiilisuutta tai epävakautta missä tahansa mittakaavassa.