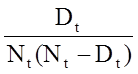Eloonjäämisfunktion tai eloonjäämiskäyrän estimoinnissa on useita eri tapoja. On olemassa useita suosittuja parametrisia menetelmiä, joita käytetään eloonjäämisdatan mallintamiseen, ja ne eroavat toisistaan sen suhteen, mitä oletuksia tehdään eloonjäämisaikojen jakaumasta populaatiossa. Joitakin suosittuja jakaumia ovat eksponentti-, Weibull-, Gompertz- ja log-normaalijakaumat.2 Kenties suosituin on eksponenttijakauma, jossa oletetaan, että osallistujan todennäköisyys sairastua kiinnostavaan tapahtumaan on riippumaton siitä, kuinka kauan hän on ollut tapahtumasta vapaa. Muissa jakaumissa tehdään erilaisia oletuksia yksilön todennäköisyydestä sairastua tapahtumaan (eli se voi kasvaa, pienentyä tai muuttua ajan myötä). Yksityiskohtaisempia tietoja eloonjäämisanalyysin parametrisista menetelmistä löytyy teoksista Hosmer ja Lemeshow sekä Lee ja Wang1,3.

Keskitymme tässä yhteydessä kahteen ei-parametriseen menetelmään, jotka eivät tee oletuksia siitä, miten todennäköisyys, että henkilö sairastuu tapahtumaan, muuttuu ajan kuluessa. Ei-parametristen menetelmien avulla estimoidaan ja piirretään eloonjäämisjakauma tai eloonjäämiskäyrä. Eloonjäämiskäyrät esitetään usein porrasfunktioina, kuten alla olevassa kuvassa on esitetty. Aika on esitetty X-akselilla ja eloonjääminen (riskiryhmään kuuluvien henkilöiden osuus) Y-akselilla. Huomaa, että eloonjääneiden prosenttiosuus ei aina vastaa elossa olevien prosenttiosuutta (jolloin oletetaan, että kiinnostava lopputulos on kuolema). “Selviytyminen” voi tarkoittaa myös osuutta, joka on vapaa jostakin muusta lopputulostapahtumasta (esim. prosenttiosuus, joka on vapaa sydäninfarktista tai sydän- ja verisuonitaudista), tai se voi edustaa myös prosenttiosuutta, joka ei koe tervettä lopputulosta (esim. syövän remissiota).

Eloonjäämisfunktio

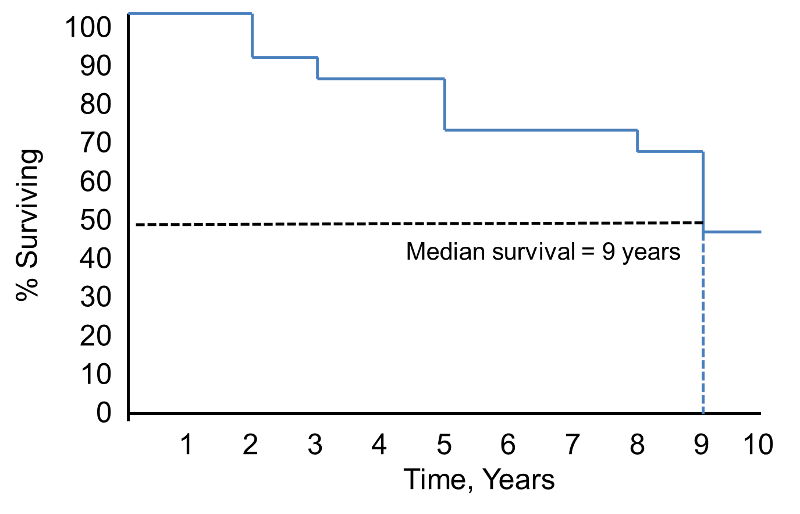
Huomaa, että selviytymistodennäköisyys on 100 % kahden vuoden ajan ja laskee sitten 90 %:iin. Eloonjäämisen mediaani on 9 vuotta (eli 50 % väestöstä selviytyy 9 vuotta; ks. katkoviivat).

Esimerkki:

Harkitaan pientä prospektiivista kohorttitutkimusta, jonka tarkoituksena on tutkia aikaa kuolemaan. Tutkimukseen osallistuu 20 osallistujaa, jotka ovat 65-vuotiaita tai vanhempia; heidät rekisteröidään viiden vuoden aikana ja heitä seurataan enintään 24 vuoden ajan, kunnes he kuolevat, tutkimus päättyy tai he keskeyttävät tutkimuksen (lost to follow-up). Tiedot esitetään jäljempänä. Tutkimuksessa on 6 kuolemantapausta ja 3 osallistujaa, joiden seuranta on päättynyt kokonaan (eli 24 vuotta). Lopuilla 11:llä on alle 24 vuoden seuranta-aika, mikä johtuu myöhäisestä ilmoittautumisesta tai seurantakadosta.

Osallistujan tunnistenumero	kuoleman vuosi	vuosi. Viimeinen yhteydenotto
1		24
2	3
3		11
4		19
5		24
6		13
7	14
8		2
9		18
10		17
11		24
12		21
13		12
14	1
15		10
16	23
17		6
18	5
19		9
20	17

elinaikataulu (aktuaarinen taulukko)

Eräs tapa tiivistää osallistujien kokemukset on elinaikataulu, tai vakuutusmatemaattisen taulukon avulla. Elinaikatauluja käytetään usein vakuutusalalla elinajanodotteen arvioimiseen ja vakuutusmaksujen määrittämiseen. Keskitymme tietyntyyppiseen elinaikatauluun, jota käytetään laajalti biostatistisissa analyyseissä ja jota kutsutaan kohortin elinaikatauluksi tai seurantaelinaikatauluksi. Seurantaelinaikataulussa esitetään yhteenveto osallistujien kokemuksista ennalta määritellyn seurantajakson aikana kohorttitutkimuksessa tai kliinisessä tutkimuksessa siihen asti, kun kiinnostava tapahtuma tapahtuu tai tutkimus päättyy, riippuen siitä, kumpi tapahtuu ensin.

Elinaikataulukon rakentamiseksi järjestetään ensin seuranta-ajat tasaisin väliajoin. Yllä olevassa taulukossa seuranta-aika on enintään 24 vuotta, ja tarkastelemme viiden vuoden aikavälejä (0-4, 5-9, 10-14, 15-19 ja 20-24 vuotta). Laskemme yhteen niiden osallistujien määrän, jotka ovat elossa kunkin jakson alussa, niiden määrän, jotka kuolevat, ja niiden määrän, jotka sensuroidaan kullakin jaksolla.

Intervalli vuosina	Välin alussa elossa olevien määrä	Kuolleiden määrä välin aikana	Sensuroitujen määrä
0-4	20	2	1
5-9	17	1	2
10-14	14	1	4
15-19	9	1	3
20-24	5	1	4

Käytämme elintapa-analyysissämme seuraavaa notaatiota. Määrittelemme ensin notaation ja käytämme sitä sitten elinaikataulukon rakentamiseen.

• Nt = niiden osallistujien lukumäärä, jotka ovat tapahtumavapaita ja joita pidetään riskiryhmään kuuluvina aikavälillä t (esim, tässä esimerkissä elossa olevien määrä, koska kiinnostava lopputulos on kuolema)
• Dt = niiden osallistujien määrä, jotka kuolevat (tai kärsivät kiinnostavasta tapahtumasta) ajanjakson t aikana
• Ct = niiden osallistujien määrä, jotka sensuroidaan ajanjakson t aikana Nt* = riskiryhmään kuuluvien osallistujien keskimääräinen määrä ajanjakson t aikana
• Nt* = riskiryhmään kuuluvien osallistujien keskimääräinen määrä ajanjakson t aikana [Vakuutusmatemaattisia elinaikataulukoita konstruoitaessa käytetään usein seuraavia oletuksia: Ensinnäkin oletetaan, että kiinnostavat tapahtumat (esim. kuolemantapaukset) tapahtuvat ajanjakson lopussa ja että sensuroidut tapahtumat tapahtuvat tasaisesti (tai tasaisesti) koko ajanjakson aikana. Tämän vuoksi Nt:hen tehdään usein mukautus, joka kuvastaa riskissä olevien osallistujien keskimääräistä lukumäärää jakson aikana, Nt*, joka lasketaan seuraavasti: Nt* =Nt-Ct/2 (ts., vähennetään puolet sensuroiduista tapahtumista).
• qt = kuolevien (tai tapahtumasta kärsivien) osuus ajanjakson t aikana, qt = Dt/Nt*
• pt = eloonjääneiden (tapahtumasta vapaana pysyvien) osuus ajanjakson t aikana, pt = 1-qt
• St, eloonjääneiden (tai tapahtumasta vapaana pysyvien) osuus ajanjakson t jälkeen; tätä kutsutaan toisinaan nimellä kumulatiivinen eloonjäämistodennäköisyys, ja se lasketaan seuraavasti: Ensin määritellään niiden osallistujien osuus, jotka selviytyvät ajankohdan 0 (aloitusajankohta) jälkeen, seuraavasti: S0 = 1 (kaikki osallistujat elossa tai tapahtumasta vapaita ajankohtana nolla eli tutkimuksen aloitusajankohtana). Kunkin myöhemmän ajanjakson jälkeen eloonjääneiden osuus lasketaan käyttäen ehdollisen todennäköisyyden periaatteita, jotka esiteltiin moduulissa Todennäköisyys. Tarkemmin sanottuna todennäköisyys sille, että osallistuja jää eloon ajanjakson 1 jälkeen, on S1 = p1. Todennäköisyys, että osallistuja selviytyy ajanjakson 2 jälkeen, tarkoittaa, että hänen oli selviydyttävä ajanjakson 1 jälkeen ja ajanjakson 2 läpi: S2 = P(selviytyminen ajanjakson 2 jälkeen) = P(selviytyminen ajanjakson 2 läpi)*P(selviytyminen ajanjakson 1 jälkeen), tai S2 = p2*S1. Yleisesti ottaen St+1 = pt+1*St.

Seurantaelinaikataulukon muoto on esitetty alla.

Ensimmäiselle aikavälille, 0-4 vuotta: Ajankohtana 0, ensimmäisen intervallin (0-4 vuotta) alussa, on 20 osallistujaa elossa tai riskiryhmässä. Kaksi osallistujaa kuolee intervallin aikana ja yksi sensuroidaan. Sovelletaan korjausta kyseisen ajanjakson aikana sensuroitujen osallistujien lukumäärää varten, jolloin saadaan Nt* =Nt-Ct/2 = 20-(1/2) = 19,5. Muiden sarakkeiden laskelmat esitetään taulukossa. Todennäköisyys sille, että osallistuja jää eloon yli 4 vuoden eli ensimmäisen intervallin jälkeen (kun käytetään intervallin ylärajaa ajan määrittelyyn) on S4 = p4 = 0,897.

Toisen intervallin, 5-9 vuoden, osalta: Riskiluku on edellisen aikavälin (0-4 vuotta) riskiluku, josta on vähennetty ne, jotka kuolevat ja jotka on sensuroitu (eli Nt = Nt-1-Dt-1-Dt-1-Ct-1 = 20-2-1 = 17). Todennäköisyys sille, että osallistuja selviytyy yli 9 vuotta on S9 = p9*S4 = 0,937*0,897 = 0,840.

Intervalli vuosina	Riskissä olevien lukumäärä väliajalla, Nt	Keskimääräinen riskissä olevien lukumäärä väliajalla, Nt*	Kuolleiden määrä väliajalla, Dt	Seurantaan kadonneet, Ct	Kuolemien osuus Välin aikana, qt	Riskiryhmään kuuluvien osuus elossa Interval, pt	Survival Probability St
0-4	20	20-(1/2) = 19.5	2	1	2/19.5 = 0.103	1-0.103 = 0.897	1(0.897) = 0.897
5-9	17	17-(2/2) = 16.0	1	2	1/16 = 0.063	1-0.063 = 0.937	(0.897)(0.937)=0.840

Täydellinen seurantaelämän taulukko on esitetty alla.

Intervalli vuosina	Riskialttiiden määrä intervallin aikana, Nt	Keskimääräinen riskialttiiden määrä intervallin aikana, Nt*	Kuolleiden määrä väliajalla, Dt	Seurantaan kadonneet, Ct	Proportion Dying During Interval, qt	Among those at Risk, Proportion Surviving Interval,pt	Survival Probability St
0-4	20	19.5	2	1	0.103	0.897	0.897
5-9	17	16.0	1	2	0.063	0.937	0.840
10-14	14	12.0	1	4	0.083	0.917	0.770
15-19	9	7.5	1	3	0.133	0.867	0.668
20-24	5	3.0	1	4	0.333	0.667	0.446

Tässä taulukossa käytetään vakuutusmatemaattista menetelmää seurantakäyntiaikataulukon muodostamiseen, jossa aika on jaettu tasaisin väliajoin.

Kaplan-Meierin (Product Limit) lähestymistapa

Yllä esitetyn elinaikataulukon lähestymistavan ongelmana on se, että eloonjäämistodennäköisyydet voivat muuttua sen mukaan, miten aikavälit on järjestetty, erityisesti pienillä otoksilla. Kaplan-Meier-lähestymistapa, jota kutsutaan myös nimellä product limit -lähestymistapa, on suosittu lähestymistapa, joka ratkaisee tämän ongelman arvioimalla eloonjäämistodennäköisyyden uudelleen aina, kun tapahtuma sattuu.

Kaplan-Meier-lähestymistavan tarkoituksenmukainen käyttö perustuu olettamukseen, että sensurointi on riippumaton kiinnostavan tapahtuman todennäköisyydestä ja että eloonjäämistodennäköisyyksien todennäköisyydet ovat vertailukelpoisia osanottajilla, jotka rekrytoitiin varhaisessa vaiheessa ja myöhemmin tutkimukseen. Kun verrataan useita ryhmiä, on myös tärkeää, että nämä oletukset täyttyvät kussakin vertailuryhmässä ja että esimerkiksi sensurointi ei ole todennäköisempää yhdessä ryhmässä kuin toisessa.

Alla olevassa taulukossa käytetään Kaplan-Meier-menetelmää samojen tietojen esittämiseen, jotka esitettiin edellä elinaikataulukkomenetelmää käyttäen. Huomaa, että aloitamme taulukon ajalla Time=0 ja Survival Probability = 1. Ajankohtana = 0 (lähtötilanne tai tutkimuksen alku) kaikki osallistujat ovat vaarassa ja eloonjäämistodennäköisyys on 1 (tai 100 %). Kaplan-Meierin lähestymistavassa eloonjäämistodennäköisyys lasketaan käyttämällä St+1 = St*((Nt+1-Dt+1)/Nt+1). Huomattakoon, että Kaplan-Meier-menetelmää käyttävät laskelmat ovat samanlaisia kuin vakuutusmatemaattista elinaikataulua käyttävät laskelmat. Suurin ero on aikaväleissä, eli vakuutusmatemaattisen elinaikataulukon lähestymistavassa tarkastellaan tasaisin väliajoin annettuja aikavälejä, kun taas Kaplan-Meierin lähestymistavassa käytetään havaittuja tapahtuma-aikoja ja sensurointiaikoja. Eloonjäämistodennäköisyyksien laskelmat on esitetty yksityiskohtaisesti taulukon ensimmäisillä riveillä.

Kaplan-Meierin lähestymistapaa käyttävä elinaikataulukko

Aika, Years	Number at Risk Nt	Number of Deaths Dt	Sensuroitujen määrä Ct	Selviytymistodennäköisyys St+1 = St*((Nt+1-Dt+1)/Nt+1)
0	20				1
1	20	1		1*((20-1)/20) = 0.950
2	19		1	0.950*((19-0)/19)=0.950
3	18	1		0.950*((18-1)/18) = 0.897
5	17	1		0.897*((17-1)/17) = 0.844
6	16		1	0.844
9	15		1	0.844
10	14		1	0.844
11	13		1	0.844
12	12		1	0.844
13	11		1	0.844
14	10	1		0.760
17	9	1	1	0.676
18	7		1	0.676
19	6		1	0.676
21	5		1	0.676
23	4	1		0.507
24	3			3	0.507

Suurilla aineistojoukoilla nämä laskutoimitukset ovat työläitä. Nämä analyysit voidaan kuitenkin tuottaa SAS:n kaltaisilla tilastollisilla laskentaohjelmilla. Excel-ohjelmaa voidaan käyttää myös eloonjäämistodennäköisyyksien laskemiseen, kun aineisto on järjestetty ajankohtien mukaan ja tapahtumien lukumäärät ja sensuroidut ajankohdat on koottu yhteen.

Elinaikataulusta voidaan tuottaa Kaplan-Meierin eloonjäämiskäyrä.

Kaplan-Meierin eloonjäämiskäyrä yllä oleville tiedoille

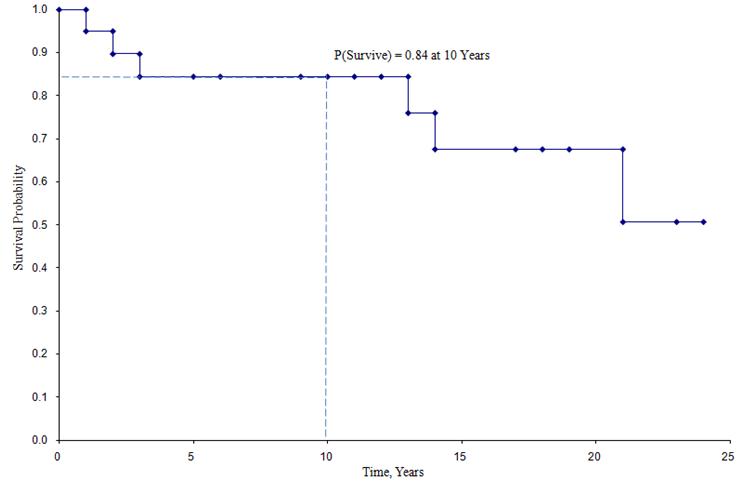
Yllä esitetyssä eloonjäämiskäyrässä symbolit edustavat kutakin tapahtuma-aikaa, joko kuolemaa tai sensuroitua aikaa. Eloonjäämiskäyrästä voidaan myös arvioida todennäköisyys sille, että osallistuja selviytyy 10 vuoden jälkeen, sijoittamalla 10 vuotta X-akselille ja lukemalla Y-akselille ylös ja yli. Niiden osallistujien osuus, jotka selviytyvät 10 vuoden jälkeen, on 84 %, ja niiden osallistujien osuus, jotka selviytyvät 20 vuoden jälkeen, on 68 %. Eloonjäämisen mediaani arvioidaan sijoittamalla 0,5 Y-akselille ja lukemalla X-akselin yli ja alas. Eloonjäämisajan mediaani on noin 23 vuotta.

Eloonjäämistodennäköisyyksien keskivirheet ja luottamusvälin arviot

Nämä arviot eloonjäämistodennäköisyyksistä tiettyinä ajankohtina ja eloonjäämisajan mediaanista ovat piste-estimaatteja, ja niitä on tulkittava sellaisina. Eloonjäämistodennäköisyyksien keskivirheiden ja luottamusvälin estimaattien tuottamiseksi on olemassa kaavoja, jotka voidaan tuottaa monilla tilastollisilla laskentapaketeilla. Suosittu kaava eloonjäämisestimaattien keskivirheen arvioimiseksi on nimeltään Greenwoodin5 kaava, ja se on seuraava:

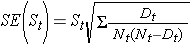
Suuruus 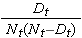summataan riskissä olevien lukumäärille (Nt) ja kuolemantapausten lukumäärille (Dt), jotka tapahtuvat kiinnostavana ajankohtana (eli kumulatiivisesti, kaikkien ajankohtien yli ennen kiinnostavaa ajankohtaa, ks. esimerkki alla olevassa taulukossa). Jäljempänä olevassa taulukossa esitettyjen tietojen eloonjäämisestimaateille on laskettu keskivirheet. Huomaa, että viimeisessä sarakkeessa on luku 1,96*SE(St), joka on virhemarginaali ja jota käytetään 95 prosentin luottamusvälin estimaattien laskemiseen (eli St ± 1,96 x SE(St)).

Eloonjäämisarvioiden keskivirheet

Aika, Years	Number at Risk Nt	Number of Deaths Dt	Survival Todennäköisyys St				1.96*SE (St)
0	20		1		1
1	20	1	0.950	0.003	0.003	0.049	0.096
2	19		0.950	0.000	0.003	0.049	0.096
3	18	1	0.897	0.003	0.006	0.069	0.135
5	17	1	0.844	0.004	0.010	0.083	0.162
6	16		0.844	0.000	0.010	0.083	0.162
9	15		0.844	0.000	0.010	0.083	0.162
10	14		0.844	0.000	0.010	0.083	0.162
11	13		0.844	0.000	0.010	0.083	0.162
12	12		0.844	0.000	0.010	0.083	0.162
13	11		0.844	0.000	0.010	0.083	0.162
14	10	1	0.760	0.011	0.021	0.109	0.214
17	9	1	0.676	0.014	0.035	0.126	0.246
18	7		0.676	0.000	0.035	0.126	0.246
19	6		0.676	0.000	0.676	0.000	0.035	0.126	0.246
23	4	1	0.507	0.083	0.118	0.174	0.341
24	3		0.507	0.000	0.118		0.174	0.341

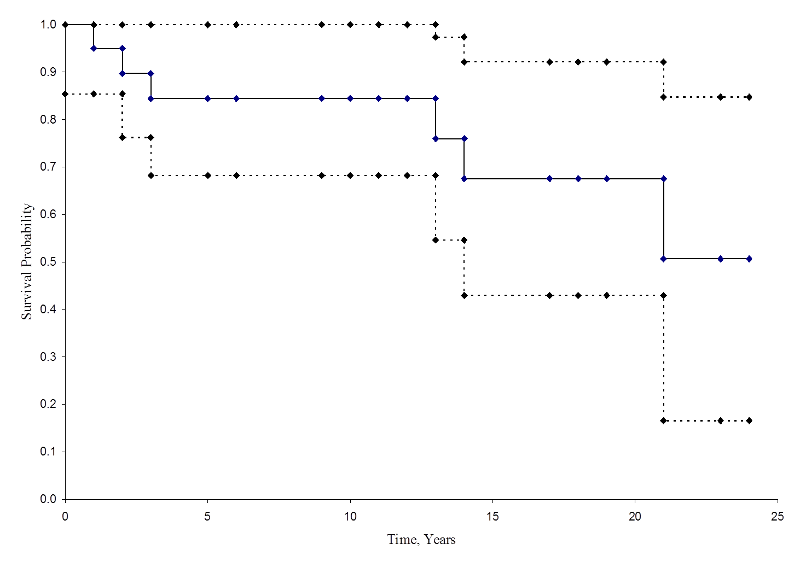
Alhaalla olevassa kuviossa on esitetty yhteenvetona alla olevassa kuviossa esitettyjä estimaatteja ja niiden luotettavuusalueita. Kaplan-Meierin eloonjäämiskäyrä on esitetty yhtenäisenä viivana, ja 95 prosentin luottamusrajat on esitetty katkoviivoina.

Kaplan-Meierin eloonjäämiskäyrä luottamusväleineen

Kumulatiiviset ilmaantuvuuskäyrät

Jotkut tutkijat haluavat luoda kumulatiivisia ilmaantuvuuskäyriä, toisin kuin eloonjäämiskäyriä, jotka osoittavat kumulatiiviset todennäköisyydet kokea kiinnostava tapahtuma. Kumulatiivinen ilmaantuvuus eli kumulatiivinen epäonnistumistodennäköisyys lasketaan muodossa 1-St, ja se voidaan helposti laskea elinaikataulusta Kaplan-Meierin lähestymistapaa käyttäen. Edellä esitetyn esimerkin kumulatiiviset vikaantumistodennäköisyydet on esitetty alla olevassa taulukossa.

Life Table with Cumulative Failure Probabilities

Aika, Years	Number at Risk Nt	Number of Deaths Dt	Number Censored Ct	Survival Probability St	Failure Probability 1-St
0	20					1	0
1	20	1		0.950	0.050
2	19		1	0.950	0.050
3	18	1		0.897	0.103
5	17	1		0.844	0.156
6	16		1	0.844	0.156
9	15		1	0.844	0.156
10	14		1	0.844	0.156
11	13		1	0.844	0.156
12	12		1	0.844	0.156
13	11		1	0.844	0.156
14	10	1		0.760	0.240
17	9	1	1	0.676	0.324
18	7		1	0.676	0.324
19	6		1	0.676	0.324
21	5		1	0.676	0.324
23	4	1		0.507	0.493
24	3		3	0.507	0.493

Alla olevassa kuvassa on esitetty edellä kuvattuun tutkimukseen osallistuneiden osallistujien kumulatiivinen kuoleman esiintyvyys.

Kumulatiivinen ilmaantuvuuskäyrä

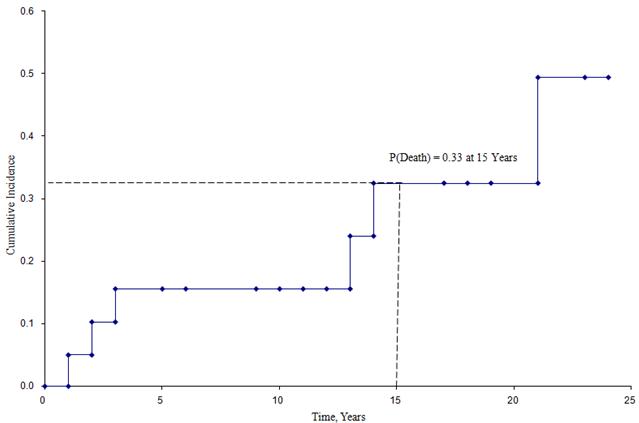
Tästä kuviosta voidaan arvioida todennäköisyys, että osallistuja kuolee tiettyyn ajankohtaan mennessä. Esimerkiksi kuoleman todennäköisyys on noin 33 % 15 vuoden iässä (ks. katkoviivat).

palaa alkuun | edellinen sivu | seuraava sivu