Alussa on yleensä tarpeen saada käsitys syklin pV-kaaviosta. Tätä varten jäljitämme isokoorisen ja adiabaattisen prosessin käyrät. Otto-syklin likimääräinen kuvaaja on esitetty seuraavassa kuvassa.

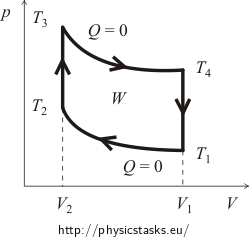
Syklin hyötysuhde η määritellään seuraavasti:

\

joissa W on kaasun yhden syklin aikana tekemä työ, josta on vähennetty ulkopuolisten voimien tekemä työ (kaaviossa sitä kuvaa syklin viivojen määrittelemä pinta-ala!) ja Qsup on systeemiin syklin aikana syötetty lämpö.

Työ W voidaan laskea käyttämällä paineen ja tilavuuden välistä suhdetta adiabaattisen paisumisen ja puristumisen aikana (isokoorisen prosessin aikana suoritettu työ on luonnollisesti nolla). Tässä tehtävässä on kuitenkin parempi käyttää sitä tosiasiaa, että sisäenergian kokonaismuutoksen sykliä kohti on oltava yhtä suuri kuin nolla (palaamme takaisin samaan tilaan kuin alussa, joten lämpötila ja siten sisäenergia pysyvät samana!). Ensimmäisen termodynaamisen lain mukaan kaasun tekemä työ voidaan ilmaista syötetyn lämmön Qsup ja vapautuneen lämmön Qrel erotuksena. Kierron hyötysuhteen kaava on siis muotoa

\

Aluksi lasketaan syötetty lämpö Qsup. On selvää, että adiabaattisen prosessin aikana ei tapahdu lämmönvaihtoa ja isokoorisen jäähdytyksen aikana lämpöä vapautuu. Tämä tarkoittaa, että lämpöä syötetään vain isokorisen lämmityksen aikana lämpötilasta T2 lämpötilaan T3. Tämän lämmön määrä voidaan ilmaista kaasun ainemäärän n ja sen molaarisen lämpökapasiteetin CV muuttujina seuraavasti:

\

ilmaisemme vapautuvan lämmön määrän Qrel suunnilleen samalla tavalla. Tiedämme jo, että lämpöä vapautuu vain isokoorisen jäähtymisen aikana lämpötilasta T4 takaisin alkulämpötilaan T1. On totta, että:

\

Nyt korvaamme nämä kaavat syklin hyötysuhteen kaavaan ja saamme välittömästi:

\ \ \

Nyt meidän on ilmaistava lämpötilaerot käyttämällä annettua puristussuhdetta

\

ja Poissonin lukua κ.

Tätä varten käytämme adiabaattisen prosessin läpikäyvän ideaalikaasun yhtälöä (Poissonin laki) pVκ = C = konst.., jossa C on vakio. Nyt arvioimme paineen ideaalikaasun tilayhtälöstä

\

, jonka korvaamme Poissonin lailla. Nyt siirretään vakiot (C ja K) toiselle puolelle

\

Nyt sovelletaan tätä Poissonin lakia molemmille adiabaattisille prosesseille. Adiabaattiselle laajenemiselle saamme suhteen

\

Ja adiabaattiselle kokoonpuristumiselle saamme

\

Nyt vähennetään toinen yhtälö ensimmäisestä ja kerrotaan V1κ – 1 toisella puolella ja V2κ – 1 toisella puolella. Saamme:

\ \ \

Voidaan todeta, että olemme itse asiassa onnistuneet ilmaisemaan lämpötilaerot käyttämällä annettuja arvoja. Nyt korvaamme tämän suhteen hyötysuhteen kaavaan ja saamme lopullisen yhtälön:

\ \ \ \