Kolmogorov-Smirnovin testi

K-S-testi on sovitettavuuden hyvyystesti, jota käytetään arvioimaan aineistojakaumien yhtenäisyyttä. Se kehitettiin vastauksena khiin neliö -testin puutteisiin, sillä se tuottaa tarkkoja tuloksia vain diskreeteille, niputetuille jakaumille. K-S-testin etuna on se, että se ei tee oletuksia vertailtavien tietokokonaisuuksien jakamisesta, mikä poistaa binäärien valintaan liittyvän mielivaltaisuuden ja informaation menetyksen.

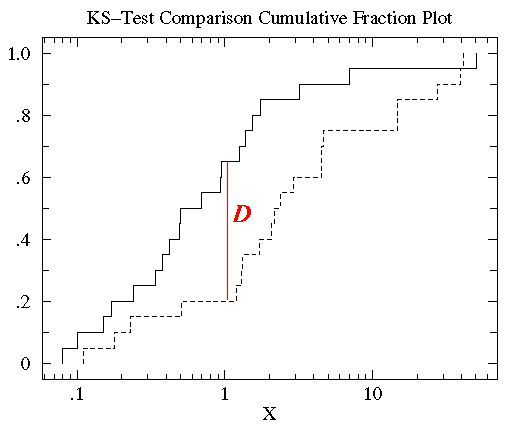
Tilastotieteessä K-S-testi on hyväksytty testi, jolla mitataan yhden muuttujan funktiona olevien jatkuvien datajoukkojen (jakamattomien datajakaumien) välisiä eroja. Tämä eromitta, K-S \(D\)-tilasto, määritellään kahden kumulatiivisen jakaumafunktion välisen absoluuttisen eron maksimiarvona. Yksipuolisella K-S-testillä verrataan tietoaineistoa tunnettuun kumulatiiviseen jakaumanfunktioon, kun taas kaksipuolisella K-S-testillä verrataan kahta eri tietoaineistoa. Kukin aineisto antaa erilaisen kumulatiivisen jakaumafunktion, ja sen merkitys perustuu sen suhteeseen todennäköisyysjakaumaan, josta aineisto on poimittu: yhden riippumattoman muuttujan \(x\) todennäköisyysjakaumafunktio on funktio, joka määrittää todennäköisyyden kullekin \(x\):n arvolle. Tietyn arvon \(x_{i}\) oletettu todennäköisyys on todennäköisyysjakaumafunktion arvo kohdassa \(x_{i}\), ja sitä merkitään \(P(x_{i})\).Kumulatiivinen jakaumafunktio määritellään funktioksi, joka antaa tietyn arvon \(x_{i}\) vasemmalla puolella olevien datapisteiden osuuden, \(P(x <x_{i})\); se edustaa todennäköisyyttä, että \(x\) on pienempi tai yhtä suuri kuin tietty arvo \(x_{i}\).

Verrattaessa siis kahta erilaista kumulatiivista jakaumafunktiota \(S_{N1}(x)\) ja \(S_{N2}(x)\), K-S-statistiikka on

D = max|S_N1(x) – S_N2(x)|

missä \(S_{N}(x)\) on kumulatiivinen jakaumafunktio todennäköisyysjakaumalle, jolta poimitaan tietokokonaisuus, jossa on \(N \)- tapahtumia. Jos \(N\) järjestettyjä tapahtumia sijaitsee datapisteissä \(x_{i}\), missä \(i = 1, \ldots, N\), niin

S_N(x_i) = (i-N)/N

missä \(x\)-datajoukko on lajiteltu kasvavaan järjestykseen. Tämä on askelfunktio, joka kasvaa \(1/N\):llä jokaisen järjestetyn datapisteen arvolla.

Tarkoituksenamme on verrata kahta jakaumaa: saapumisaikojen mitattua jakaumaa ja kertynyttä osuutta kuluneesta aikavälistä. Jos nollahypoteesi (ei vaihtelua) pitää paikkansa, saamme 50 % tapahtumista 50 %:ssa kuluneesta ajasta, ja \(D\)-tilaston pitäisi jakaantua Kolmogorovin jakauman mukaisesti monille saapumisaikajakauman realisaatioille. Testin palauttama todennäköisyys on siis \(p_{KS} = 1 – \alpha\), jossa \(\alpha\) on todennäköisyys (Kolmogorovin jakauman mukaan), että \(D\) arvo on suurempi tai yhtä suuri kuin mitattu arvo. Pieni \(p_{KS}\)-arvo osoittaa siis yhdenmukaisuutta nollahypoteesin kanssa, kun taas suuri \(p_{KS}\)-arvo osoittaa, että tapahtumien välinen aika ei ole vakio, ja siksi voidaan päätellä vaihtelua.