Maailmojen sodassa jättimäiset muukalaisrobotit nousevat maasta ja alkavat höyrystää suuria määriä näyttelijöitä. Noissa kohtauksissa on paljon mistä pitää, mutta on kolme asiaa, joita en voinut sietää.
Kuten ne kolme jalkaa, joilla ne kävelivät ympäriinsä. Ei niiden hauraalta näyttävää selkärangattomuutta, vaan niiden todellista kolmijalkaisuutta.
Please get Tom Cruise first, please get Tom Cruise first, please get …
Pitäisi olla enemmän jalkoja. Noin kuusi niitä erityisesti.
“Kuule”, saatat vastata, “se on muukalaisalus, ja kuka tietää, millaisia periaatteita he ovat löytäneet.”
Totta kai se on mahdollista. Mutta toinen tapa tarkastella asiaa on se, että meitä maan asukkaita on hyvin monenlaisia vartalo- ja raajasuunnitelmia, ja silti emme löydä kolmijalkaista mallia mistään. Ehkä se on hyvä argumentti sille, että avaruusolennot eivät rakentaisi laivaa, jossa olisi kolme jalkaa.
Mitä me maankaltaiset teemme raajojen suunnittelun suhteen?
Meillä on taipumus noudattaa lakia, joka saattaa leikata kaikkia eläinheimoja, lakia, jonka julkaisin ensimmäisen kerran Journal of Theoretical Biology -lehdessä vuonna 2001 , ja jota käsittelin tarkemmin ensimmäisessä kirjassani The Brain from 25,000 Feet .
Tämä “raajojen laki” suhteuttaa eläimen raajojen lukumäärän näiden raajojen pituuteen (suhteessa kehon kokoon).
Kun eläimen raajat ovat hyvin pitkät suhteessa sen kehon kokoon, väitin, että optimaalinen kurottautumisratkaisu (joka käyttää vähiten “rautalankaa” eli raajojen materiaalia) on, että eläimellä on noin kuusi raajaa. (Tämä koskee eläimiä, joiden raajat suuntautuvat suunnilleen säteittäisesti kehän ympäri. Eläimillä, joiden raajojen suunnat jakautuvat tasaisesti pallonmuotoiselle pinnalle, raajojen odotettu lukumäärä olisi tässä tapauksessa noin 12.)
Kun eläimen raajat lyhenevät suhteessa ruumiin kokoon, raajojen odotettu lukumäärä nousee, ja raajojen lukumäärä on valtava, kun raajat ovat hyvin lyhyitä. (Muuten, käärmeellä on johdonmukaisesti äärettömän monta äärettömän lyhyttä raajaa – eli ei yhtään raajaa.)
Yleisemmin laki ennustaa, että eläimen raajojen lukumäärä on kääntäen verrannollinen raajojen suhteelliseen pituuteen. Ja tarkemmin sanottuna laki ennustaa tietyn suhteellisuusvakion, niin että “kuusi” on ratkaisu todella pitkien raajojen tapauksessa.
Jos L on raajojen pituus ja R eläimen ruumiin säde, niin k = L / (L + R) on raajojen suhteellinen pituus eli “raajasuhde”.
Rajojen lukumäärän N odotetaan vaihtelevan suunnilleen seuraavasti:
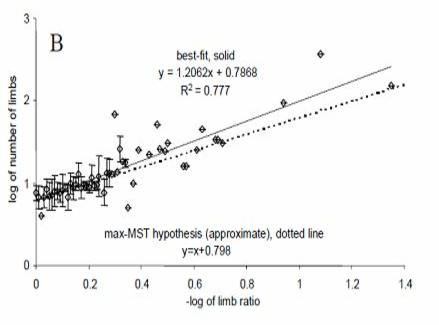
Alla olevasta kuvasta (ensimmäisestä kirjastani) käy ilmi, miten raajojen lukumäärä itse asiassa suhteutuu raajasuhteeseen 190 lajin osalta seitsemästä eläinheimosta (Annelida, Arthropoda, Cnidaria, Echinodermata, Mollusca, Vertebrata ja Tardigrada).
Ennustettu trendi on esitetty yhtenäisellä viivalla, joka on yhdenmukainen juuri edellä näkemämme N ≈ 6,28k-1 -yhtälön kanssa.
Tosiasiallinen trendi on esitetty katkoviivalla, mikä johtaa empiiriseen yhtälöön N ≈6,24k-1,17 … eli hyvin lähelle ennustetta.
Jos haluat saada paremman käsityksen raajojen laista, jota maapallon asukkaat näyttävät noudattavan, käy katsomassa tätä Eric Bolzin pientä dynaamista visuaalista ohjelmaa, jonka avulla voit vaihdella raajojen pituutta ja seurata, miten raajojen lukumäärä vaihtelee: http://www.changizi.com/limb.html Oikealla pystyakselilla voit moduloida raajojen suhdetta ja katsella, miten raajojen lukumäärä muuttuu. Ala-akselin avulla voit tehdä pidempiä tai lyhyempiä olentoja. Vasemman pystyakselin avulla voit vain muuttaa olion kokoa sivulla.
Maailmojen sodan muukalaisaluksilla pitäisi olla – ottaen huomioon niiden pitkät raajojen pituudet ja olettaen, että niitä pitäisi käsitellä suunnilleen kehän ympäri osoittavina – noin kuusi raajaa. Ei kolmea.
Sen takia ne näyttävät niin hölmöiltä. Ne ovat raajojen suunnittelualueen makean pisteen ulkopuolella.
Seuraavassa kirjoituksessani käsittelen sitä, miten tämä raaja-ajatus kertoo meille, miksi meillä on 10 sormea, ja ehkä siksi, miksi meillä on 10-sorminen lukujärjestelmä.