Tekijä Evan Ma

(Matematiikan ja fysiikan tutor The Edge Learning Centerissä)

Logaritmifunktio näyttää hämmentävän monia IB Math SL -ohjelmaa opiskelevia opiskelijoita. Jotta ymmärtäisimme sen oikein, määritellään

jossa , tiukasti positiivinen reaaliluku, on nimeltään perusta ja on potenssi. Me kaikki tiedämme esimerkiksi seuraavat ulkoa:

ja niin edelleen. Logaritmifunktio tekee sen päinvastoin – kun argumenttina on luku, se antaa potenssin, jolle on annettu tietty perusta, ja siksi se määritellään seuraavasti.

Jos

jos

Siten on selvää, että

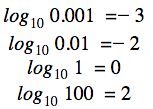
ja niin edelleen. Tarkastellaan muita esimerkkejä, joissa on mukana muita emäksiä:

Vastaamme harjoituksena seuraavat kysymykset: (a) , (b) , (c) , (d) . Vastaukset löytyvät tämän blogin lopusta.

Logaritmin määritelmästä näemme myös, että jos korotamme reaaliluvun peruslukua peruslogaritmilla, saamme takaisin luvun , eli

Voit kokeilla todentaa tämän käyttämällä laskinta eri kelvollisilla perusteilla. Tämä identiteetti on tärkeä, kun yritämme ratkaista logaritmiyhtälöitä, joista annetaan esimerkkejä alter.

Katsotaan nyt logaritmin sääntöjä. Logaritmin määritelmän tapaan käytämme indeksien lakeja sääntöjen johtamiseen:

1. Tuotoksen logaritmi on logaritmien summa

Todistus: Sanotaan ja , siis

2. Mr:n perus logaritmi on kertaa

Todistus: Sanotaan , siis

3. Osamäärän logaritmi on logaritmien erotus

Todistus: Sanotaan ja , joten

4. Loppusääntöä kutsutaan perusluvunmuutoskaavaksi. Käytämme esimerkkiä kaavan johtamisen apuna. Oletetaan, että haluamme tietää, millä potenssilla 2 on korotettava, jotta saadaan 50. Koska 50 ei ole kokonaisluvun 2 potenssi, vastaus ei ole kovin ilmeinen. Kirjoitamme siis

ja siis. Löytääksemme , sanotaan, että sovellamme yhtälön molempiin puoliin base-10-logaritmia, koska laskimessamme ei ehkä ole base-2-logaritminäppäintä:

Korjattuna neljään merkitsevään numeroon, :n arvo on noin 5,644. Voit itse asiassa tarkistaa vastauksesi korottamalla 2 potenssiin 5,644 nähdäksesi, että vastaus on noin 50.

Yleistääksemme ongelmaa, sanotaan, että meidän on löydettävä siten, että ja emäksinen logaritmi ei ole käytettävissämme, voimme siis sen sijaan käyttää base- logaritmia yhtälön

mukaisesti ja näin ollen

Tarkastellaan esimerkiksi seuraavaa. Oletetaan, että 10 000 dollarin suuruinen summa talletetaan 2,5 prosentin vuotuisella korolla, jota korotetaan vuosittain. Kuinka kauan rahaa on pidettävä tilillä, jotta se kasvaa 50 000 dollariin?

Kysymykseen vastaamiseksi yritämme periaatteessa löytää sellaisen n:n, että

Koska yksinkertainen tieteellinen taskulaskimeni ei anna minun määritellä perustaksi 1.025 logaritmiselle avaimelle, minun on turvauduttava perustanmuutoskaavaan ja käytettävä perustaa 10, ja näin ollen

Koska korkoa korotetaan vuosittain, kestää 66 vuotta kasvaa vähintään 5-kertaiseksi.

Tutustuttuamme logaritmien sääntöihin, otamme käyttöön luonnollisen logaritmifunktion eli . Se on perus-, missä on merkittävä irrationaaliluku ≈2.71828 ja jonka merkitystä luonnontieteissä ja matematiikassa ei voi tarpeeksi korostaa. Näin ollen base-logaritmi määritellään seuraavasti.

Jos

ton

Seuraavaksi tarkastellaan kahta esimerkkiä, joissa tehdään yleisiä virheitä logaritmiyhtälöiden ratkaisemisessa. Katso, pystytkö tunnistamaan virheen.

Missä virhe on? Katso tarkemmin. Toisessa vaiheessa ei tietenkään voi “jakaa” logaritmia yhteenlaskumerkin yli. Muista, että logaritmin voi “jakaa” summaksi vain, jos logaritmia sovelletaan tuotteeseen, ei summaan. Oikeat vaiheet ovat siis seuraavat:

Katsotaan nyt seuraavaa esimerkkiä ja katsotaan, pystytkö tunnistamaan virheen:

Missä on virhe? Kyllä, se on toisessa vaiheessa – logaritmien osamäärä ei tietenkään ole osamäärän logaritmi. Pikemminkin voimme käyttää perustanmuutoskaavaa yksinkertaistaaksemme ensimmäistä askelta seuraavasti:

Viimeiseksi havainnollistamme, miten logaritmisääntöjä voidaan käyttää seuraavassa esitetyn ratkaisemiseen:

Voit ehkä huomata, että tuntematon esiintyy logaritmin argumentissa sekä perustana että muuttujana. Miten voimme ratkaista :n? Menetelmä riippuu edelleen logaritmisääntöjen johdonmukaisesta soveltamisesta. Ensinnäkin korotamme molemmat puolet emäksen potensseiksi, ja näin ollen

Muistat ehkä logaritmin määritelmästä, että vasemmanpuoleinen puoli tulee juuri logaritmin argumentiksi, ja näin ollen

Sovittamalla yllä oleva yhtälö uudelleen, meidän on ratkaistava

Huomatessamme, että tämä muistuttaa kvadraattia , ratkaistaan seuraavasti:

Nyt, missä on negatiivinen juuri? Koska on myös logaritmin perusta, negatiivinen juuri hylätään siis ratkaisuna. Näin ollen on lopullinen vastaus.

Katsomalla edellä mainittuja esimerkkejä huomaat ehkä, että vaikealta tuntuvan logaritmiyhtälön ratkaiseminen ei ole lainkaan vaikeaa – riittää, että sovellat logaritmisääntöjä johdonmukaisesti, ja oikea ratkaisu saadaan.

Vastaukset kysymyksiin: (a) 2 (b) 3 (c) -3 (d) -2.