The StatsTest Flow: Ennustaminen >> Jatkuva riippuvainen muuttuja >> Enemmän kuin yksi riippumaton muuttuja >> Ei toistettuja mittauksia >> Yksi riippuvainen muuttuja

Etkö ole varma, onko tämä oikea tilastollinen menetelmä? Valitse oikea menetelmä Choose Your StatsTest -työnkulun avulla.

Mikä on monimuuttujainen moninkertainen lineaarinen regressio?

Monimuuttujainen moninkertainen lineaarinen regressio on tilastollinen testi, jota käytetään ennustamaan useita tulosmuuttujia yhden tai useamman muun muuttujan avulla. Sitä käytetään myös näiden muuttujajoukkojen ja muiden muuttujien välisen numeerisen suhteen määrittämiseen. Ennustettavan muuttujan tulee olla jatkuva ja aineistosi tulee täyttää muut alla luetellut oletukset.

Monimuuttujaisen moninkertaisen lineaarisen regression oletukset

Jokaiseen tilastolliseen menetelmään liittyy oletuksia. Oletukset tarkoittavat, että aineistosi on täytettävä tietyt ominaisuudet, jotta tilastollisen menetelmän tulokset olisivat tarkkoja.

Monimuuttujaisen moninkertaisen lineaarisen regression oletukset ovat:

1. Lineaarisuus
2. Ei poikkeavia arvoja
3. Yhtäläinen jakauma yli vaihteluvälin
4. Jäännösten normaalisuus
5. Ei monikollineaarisuutta

Sukelletaanpa kuhunkin näistä erikseen.

Lineaarisuus

Muuttujien, joista olet kiinnostunut, on oltava lineaarisesti yhteydessä toisiinsa. Tämä tarkoittaa sitä, että jos piirrät muuttujat kaavioon, voit piirtää suoran viivan, joka sopii aineiston muotoon.

Ei poikkeamia

Huomiosi kohteena olevat muuttujat eivät saa sisältää poikkeamia. Lineaarinen regressio on herkkä poikkeaville arvoille eli datapisteille, joilla on epätavallisen suuria tai pieniä arvoja. Voit kertoa, onko muuttujissasi outliereitä, piirtämällä ne ja havainnoimalla, ovatko jotkin pisteet kaukana kaikista muista pisteistä.

Yhtäläinen hajonta vaihteluvälillä

Tilastotieteessä tätä kutsutaan homoskedastisuudeksi, joka kuvaa sitä, kun muuttujien hajonta vaihteluvälillä on samanlainen.

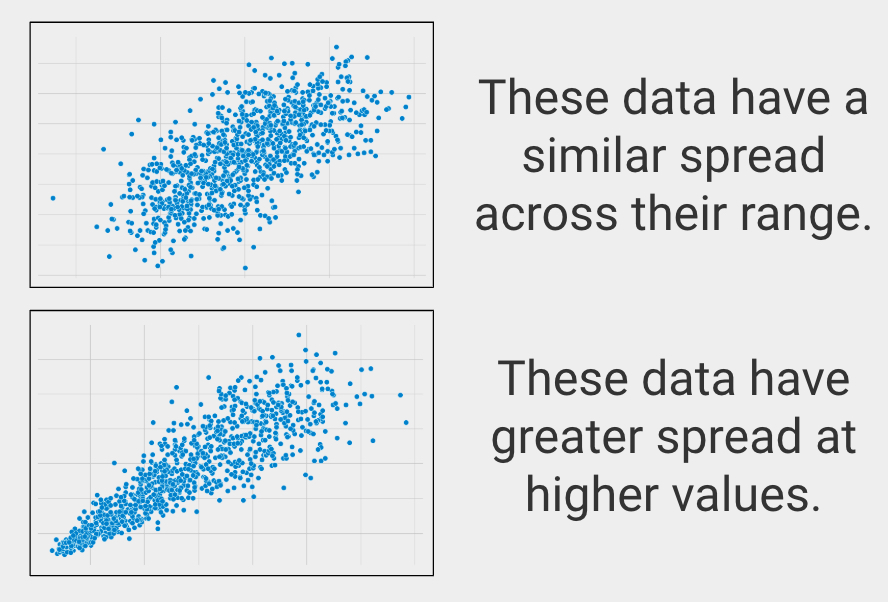
Jäännösmuuttujien normaalisuus

Sanalla “jäännösmuuttujat” viitataan arvoihin, jotka saadaan, kun todellisista arvoista vähennetään odotetut (tai ennustetut) riippuvaiset muuttujat. Näiden arvojen jakauman tulisi vastata normaalin (tai kellokäyrän) jakauman muotoa.

Tämän olettamuksen täyttyminen varmistaa, että regression tulokset ovat yhtä lailla sovellettavissa koko aineiston hajontaan ja että ennusteessa ei ole systemaattista vääristymää.

Ei monikollineaarisuutta

Monikollineaarisuudella viitataan skenaarioon, jossa kaksi tai useampi riippumatonta muuttujaa korreloi merkittävästi keskenään. Kun multikollineaarisuutta esiintyy, regressiokertoimista ja tilastollisesta merkitsevyydestä tulee epävakaita ja vähemmän luotettavia, vaikka se ei sinänsä vaikuta siihen, miten hyvin malli sopii aineistoon.

Milloin kannattaa käyttää monimuuttujaista moninkertaista lineaarista regressiota?

Monimuuttujaista moninkertaista lineaarista regressiota kannattaa käyttää seuraavassa skenaariossa:

1. Haluat käyttää yhtä muuttujaa useiden muiden muuttujien ennustamisessa tai haluat kvantifioida niiden välisen numeerisen suhteen
2. Muuttujat, joita haluat ennustaa (riippuvainen muuttujasi), ovat jatkuvia
3. Sinulla on useampi kuin yksi riippumaton muuttuja, tai yksi muuttuja, jota käytät ennustajana
4. Sinulla ei ole toistuvia mittauksia samasta havaintoyksiköstä
5. Sinulla on useampi kuin yksi riippuvainen muuttuja

selvitetään nämä, jotta tiedät, milloin kannattaa käyttää monimuuttujaista moninkertaista lineaarista regressiota.

Prediction

Etsit tilastollista testiä ennustamaan yhtä muuttujaa toisen muuttujan avulla. Tämä on ennustuskysymys. Muita analyysityyppejä ovat kahden muuttujan välisen suhteen voimakkuuden tutkiminen (korrelaatio) tai ryhmien välisten erojen tutkiminen (ero).

Jatkuva riippuva muuttuja

Muuttujan, jota haluat ennustaa, on oltava jatkuva. Jatkuva tarkoittaa, että kiinnostava muuttujasi voi periaatteessa ottaa minkä tahansa arvon, kuten sykkeen, pituuden, painon, yhden minuutin aikana syötävien jäätelöpatukoiden lukumäärän jne.

Tyyppisiä tietoja, jotka EIVÄT ole jatkuvia, ovat järjestetyt tiedot (kuten sijoittuminen kilpailussa, parhaiden yritysten sijoitukset jne.), kategoriset tiedot (sukupuoli, silmänväri, rotu jne.) tai binääriset tiedot (osti tuotteen tai ei ostanut, sairastaa tautia tai ei sairastanut jne.).

Jos riippuvainen muuttujasi on binäärinen, sinun tulisi käyttää moninkertaista logistista regressiota, ja jos riippuvainen muuttujasi on kategorinen, sinun tulisi käyttää moninomaalista logistista regressiota tai lineaarista diskriminaatioanalyysiä.

Mone than One Independent Variable

Multivariate Multiple Linear Regression (monimuuttujainen moninkertainen lineaarinen regressio) -menetelmää käytetään silloin, kun jokaiselle havaintoyksikölle on yksi tai useampi ennustemuuttuja, jolla on useita arvoja.

No Repeated Measures (ei toistettuja mittauksia)

Tämä menetelmä sopii skenaarioon, jossa jokaiselle havaintoyksikölle on vain yksi havainto. Havaintoyksikkö on se, mikä muodostaa “datapisteen”, esimerkiksi myymälä, asiakas, kaupunki jne…

Jos sinulla on yksi tai useampi riippumaton muuttuja, mutta ne mitataan samasta ryhmästä useana eri ajankohtana, sinun tulisi käyttää sekatehostemallia.

Monta kuin yhtä riippuvaista muuttujaa

Jos haluat suorittaa monimuuttujaisen moninkertaisen lineaarisen regression, sinulla on oltava useampi kuin yksi riippuvainen muuttuja eli muuttuja, jota yrität ennustaa.

Jos ennustat vain yhtä muuttujaa, sinun on käytettävä moninkertaista lineaarista regressiota.

Monimuuttujainen moninkertainen lineaarinen regressio Esimerkki

Rippuvainen muuttuja 1: Revenue
Dependent Variable 2: Customer traffic
Independent Variable 1: Mainontaan käytetyt dollarit kaupungeittain
Independent Variable 2: Kaupungin väkiluku

Nollahypoteesi, joka on tilastollista kielenkäyttöä sille, mitä tapahtuisi, jos käsittely ei tee mitään, on, että mainontaan käytetyillä dollareilla ja mainosdollareilla tai väkiluvulla kaupungeittain ei ole mitään yhteyttä. Testissämme arvioidaan, kuinka todennäköistä on, että tämä hypoteesi pitää paikkansa.

Keräämme aineistomme, ja kun olemme varmistaneet, että lineaarisen regression oletukset täyttyvät, suoritamme analyysin.

Tässä analyysissä suoritetaan käytännössä moninkertainen lineaarinen regressio kahdesti käyttäen molempia riippuvia muuttujia. Näin ollen, kun suoritamme tämän analyysin, saamme beta-kertoimet ja p-arvot jokaiselle termille “liikevaihto”-mallissa ja “asiakasliikenne”-mallissa. Kaikille lineaarisille regressiomalleille on yksi beetakerroin, joka vastaa lineaarisen regressiosuoran leikkauspistettä (usein merkitty 0:lla β0). Tämä on yksinkertaisesti se kohta, jossa regressiosuora risteää y-akselin kanssa, jos aineistosi piirretään. Kun kyseessä on moninkertainen lineaarinen regressio, on lisäksi vielä kaksi muuta beta-kerrointa (β1, β2 jne.), jotka kuvaavat riippumattomien ja riippuvaisten muuttujien välistä suhdetta.

Nämä ylimääräiset beta-kertoimet ovat avain muuttujiesi välisen numeerisen suhteen ymmärtämiseen. Pohjimmiltaan jokaisen yksikön (arvon 1) kasvun tietyssä riippumattomassa muuttujassa riippuvaisen muuttujasi odotetaan muuttuvan kyseiseen riippumattomaan muuttujaan liittyvän beetakertoimen arvolla (pitäen muut riippumattomat muuttujat vakioina).

Näihin ylimääräisiin beeta-arvoihin liittyvä p-arvo on mahdollisuus nähdä tuloksemme olettaen, että kyseisen muuttujan ja liikevaihdon välillä ei todellisuudessa ole mitään yhteyttä. P-arvo, joka on pienempi tai yhtä suuri kuin 0,05, tarkoittaa, että tuloksemme on tilastollisesti merkitsevä ja voimme luottaa siihen, että ero ei johdu pelkästään sattumasta. Saadaksemme mallin yleisen p-arvon ja yksittäiset p-arvot, jotka edustavat muuttujien vaikutuksia kahden mallin välillä, käytetään usein MANOVA-analyysejä.

Tämän analyysin tuloksena saadaan lisäksi R-ruutuarvo (R2). Tämä arvo voi vaihdella välillä 0-1 ja edustaa sitä, kuinka hyvin lineaarinen regressiosuorasi sopii datapisteisiisi. Mitä korkeampi R2-arvo on, sitä paremmin mallisi sopii aineistoihisi.

Tiheästi kysytyt kysymykset

K: Mitä eroa on monimuuttujaisella moninkertaisella lineaarisella regressiolla ja lineaarisen regression suorittamisella useaan kertaan?
A: Ne ovat käsitteellisesti samanlaisia, koska yksittäiset mallin kertoimet ovat samat molemmissa skenaarioissa. Olennainen ero on kuitenkin se, että monimuuttujaisen lineaarisen regression merkitsevyystesteissä ja luottamusväleissä otetaan huomioon useat riippuvaiset muuttujat.

Q: Miten suoritan monimuuttujaisen monimuuttujaisen lineaarisen regression SPSS:ssä, R:ssä, SAS:ssa tai STATA:ssa?
A: Tämä resurssi keskittyy auttamaan sinua valitsemaan oikean tilastollisen menetelmän joka kerta. Käytettävissä on monia resursseja, jotka auttavat sinua selvittämään, miten tämä menetelmä ajetaan tietojesi kanssa:
R-artikkeli: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/

Help!

Jos et vieläkään saa jotain selville, ota rohkeasti yhteyttä.