Graafit Pythonissa

Graafiteorian alkujuuret

Ennen kuin aloitamme varsinaisten graafien toteutusten tekemisen Pythonissa ja ennen kuin aloitamme graafeja käsittelevien Python-moduulien esittelyn, haluamme omistautua graafeja käsittelevän teorian alkulähteille.
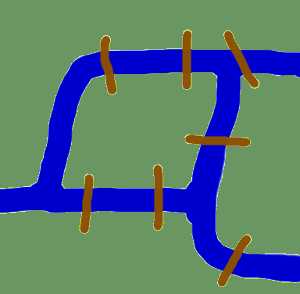
Alkujuuret vievät meidät ajassa taaksepäin 1700-luvun Künigsbergiin. Königsberg oli tuolloin kaupunki Preussissa. Pregel-joki virtasi kaupungin läpi muodostaen kaksi saarta. Kaupunki ja saaret oli yhdistetty seitsemällä sillalla, kuten kuvassa näkyy. Kaupungin asukkaita liikutti kysymys, olisiko mahdollista tehdä kävelykierros kaupungin läpi käymällä jokaisella kaupungin alueella ja ylittämällä jokainen silta vain kerran? Jokainen silta oli ylitettävä kokonaan, eli ei saa kävellä puolet sillasta ja kääntyä sitten ympäri ja myöhemmin ylittää toinen puolikas toiselta puolelta. Kävelyn ei tarvitse alkaa ja päättyä samaan paikkaan.Leonhard Euler ratkaisi ongelman vuonna 1735 osoittamalla, että se ei ole mahdollista. Hän havaitsi, että reitin valinnalla kunkin maa-alueen sisällä ei ole merkitystä ja että ainoa asia, jolla on merkitystä, on järjestys (tai järjestys), jossa sillat ylitetään. Hän oli muotoillut ongelmasta abstraktion, poistanut tarpeettomat seikat ja keskittynyt maa-alueisiin ja niitä yhdistäviin siltoihin. Näin hän loi perusteet graafiteorialle. Jos näemme “maa-alueen” kärkipisteenä ja jokaisen sillan särmänä, olemme “pelkistäneet” ongelman graafiksi.

Esittely graafiteoriaan Pythonin avulla

Ennen kuin aloitamme käsittelemään mahdollisia Python-ohjelmalla esitettäviä graafien esitystapoja, haluamme esitellä joitakin yleisiä määritelmiä graafeista ja niiden komponenteista.
Matematiikassa ja tietojenkäsittelytieteessä “graafi “1 koostuu “solmuista”, jotka tunnetaan myös nimellä “kärkipisteet”.Solmut voivat olla tai eivät voi olla yhteydessä toisiinsa. Kuvassamme, – joka on graafin kuvallinen esitys, – solmu “a” on yhteydessä solmuun “c”, mutta “a” ei ole yhteydessä solmuun “b”. Kahden solmun välistä yhdysviivaa kutsutaan reunaksi. Jos solmujen väliset reunat ovat suuntaamattomia, kuvaajaa kutsutaan suuntaamattomaksi kuvaajaksi. Jos reuna on suunnattu yhdestä pisteestä (solmusta) toiseen, kuvaajaa kutsutaan suunnatuksi kuvaajaksi. Suunnattua reunaa kutsutaan kaareksi.
Vaikka graafit saattavat näyttää hyvin teoreettisilta, monet käytännön ongelmat voidaan esittää graafien avulla. Niitä käytetään usein ongelmien tai tilanteiden mallintamiseen fysiikassa, biologiassa, psykologiassa ja ennen kaikkea tietotekniikassa. Tietojenkäsittelytieteessä graafeja käytetään kuvaamaan tietoliikenneverkkoja, tietojen organisointia, laskentalaitteita, laskennan kulkua,

Viimeisessä tapauksessa graafeja käytetään kuvaamaan tietojen organisointia, kuten käyttöjärjestelmän tiedostojärjestelmää, tai tietoliikenneverkkoja. Myös verkkosivujen linkkirakenne voidaan nähdä graafina eli suunnattuna graafina, koska linkki on suunnattu reuna tai kaari.
Pythonissa ei ole sisäänrakennettua tietotyyppiä tai -luokkaa graafeille, mutta ne on helppo toteuttaa Pythonissa. Yksi tietotyyppi on ihanteellinen kuvaajien esittämiseen Pythonissa, eli sanakirjat. Kuvassamme oleva graafi voidaan toteuttaa seuraavalla tavalla:

graph = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }

Yllä olevan sanakirjan avaimet ovat graafimme solmuja. Vastaavat arvot ovat listoja solmujen kanssa, joita yhdistää reuna. Yksinkertaisempaa ja tyylikkäämpää tapaa esittää graafi ei ole.
Särmä voidaan nähdä 2-tuplina, jonka elementteinä ovat solmut, eli (“a”, “b”)
Funktio, joka tuottaa listan kaikista reunoista:Tämä koodi tuottaa seuraavan tuloksen, jos se yhdistetään aiemmin määritettyyn graafin sanakirjaan:

 $ python3 graph_simple.py 

Kuten näemme, ei ole yhtään reunaa, joka sisältäisi solmun “f”. “f” on graafimme eristetty solmu.
Seuraava Python-funktio laskee annetun graafin eristetyt solmut:Jos kutsumme tätä funktiota graafimme kanssa, palautetaan lista, joka sisältää “f”:

Graafit Python-luokkana

Ennen kuin jatkamme funktioiden kirjoittamista graafeille, teemme ensimmäisen kokeilun Python-graafiluokan toteutuksesta. Jos katsot seuraavaa luokkamme listausta, näet __init__-metodissa, että käytämme sanakirjaa “self.__graph_dict” kärkipisteiden ja niitä vastaavien viereisten kärkipisteiden tallentamiseen.
Jos käynnistät tämän moduulin itsenäisesti, saat seuraavan tuloksen:

Polut graafeissa

Haluamme nyt löytää lyhimmän polun yhdestä solmusta toiseen solmuun. Ennen kuin tulemme Python-koodiin tätä ongelmaa varten, meidän on esitettävä joitakin muodollisia määritelmiä.
Rinnakkaiset kärjet:
Kaksi kärkeä ovat vierekkäisiä, kun molemmilla on yhteinen särmä.
Polku suuntaamattomassa kuvaajassa:
Polku suuntaamattomassa kuvaajassa on sarja kärkiä P = ( v1, v2, …., vn ) ∈ V x V x … x V siten, että vi on vierekkäin v{i+1}:n kanssa, kun 1 ≤ i < n. Tällaista polkua P sanotaan poluksi, jonka pituus on n ja joka kulkee v1:stä vn:iin.
Yksinkertainen polku:
Polkua, jossa ei ole toistuvia kärkipisteitä, sanotaan yksinkertaiseksi poluksi.
Esimerkki:
(a, c, e) on yksinkertainen polku kuvaajassamme, kuten myös (a,c,e,b). (a,c,e,b,c,d) on polku, mutta ei yksinkertainen polku, koska solmu c esiintyy kahdesti.

Seuraava metodi löytää polun alkupisteestä loppupisteeseen:
Jos tallennamme find_path-metodin sisältävän graafiluokkamme nimellä “graphs.py”, voimme tarkastaa find_path-funktiomme toimintatavan:
Edellisen ohjelman tulos näyttää tältä:
Metodi find_all_paths löytää kaikki polut alkupisteen ja loppupisteen väliltä:Muutimme hieman esimerkkigraafiamme lisäämällä reunoja “a”:sta “f”:ään ja “f:stä” “d:hen” testataksemme aiemmin määriteltyä metodia:Tulos näyttää tältä:

aste

Graafin pisteen v aste on sitä yhdistävien reunojen lukumäärä, ja silmukat lasketaan kahdesti. Vertexin v astetta merkitään deg(v). Graafin G suurin aste, jota merkitään Δ(G), ja pienin aste, jota merkitään δ(G), ovat graafin kärkien suurin ja pienin aste.
Oikeanpuoleisessa kuvaajassa maksimiaste on 5 pisteessä c ja minimiaste 0 eli eristetyssä pisteessä f.
Jos kaikki kuvaajan asteet ovat samat, kuvaaja on säännöllinen kuvaaja.
Säännöllisessä kuvaajassa kaikki asteet ovat samat, joten voidaan puhua kuvaajan asteesta.
Asteiden summan kaava (Handshaking-lemma):
∑v &in; Vdeg(v) = 2 |E|
Tämä tarkoittaa, että kaikkien kärkipisteiden asteiden summa on yhtä suuri kuin särmien lukumäärä kerrottuna 2:lla.Voimme päätellä, että parittoman asteen kärkipisteiden lukumäärän on oltava parillinen. Tämä väite tunnetaan nimellä handshaking-lemma. Nimi “kättelylemma” juontaa juurensa suositusta matemaattisesta ongelmasta: Missä tahansa ihmisryhmässä niiden ihmisten lukumäärä, jotka ovat kättelleet parittoman määrän muita ryhmään kuuluvia ihmisiä, on parillinen.
Seuraavalla metodilla lasketaan pisteen aste:
Seuraavalla metodilla lasketaan lista, joka sisältää graafin eristetyt huiput:
Menetelmillä delta ja delta voidaan laskea pienin ja suurin mahdollinen aste:

Astejärjestys

Ohjaamattoman graafin astejärjestys määritellään sen huippuasteiden järjestyksenä ei-lisäyvässä järjestyksessä.
Seuraava metodi palauttaa tuplen, jossa on instanssi-graafin astejärjestys:
Esimerkkigraafimme astejono on seuraava kokonaislukujen sarja: (5,2,1,1,1,0).
Isomorfisilla graafeilla on sama astejono. Kaksi graafia, joilla on sama astelukujärjestys, eivät kuitenkaan välttämättä ole isomorfisia.
Onkin kysymys, voidaanko tietty astejono toteuttaa yksinkertaisella graafilla. Erdös-Gallain teoreema sanoo, että n luvun di (fori = 1, …, n) on yksinkertaisen graafin astejakso, jos ja vainjos jakson summa on parillinen ja jos seuraava ehto täyttyy:

Erdös-Gallain lauseen toteutus

Meidän graafiluokkamme – ks. tarkempi luettelo alempana – sisältää metodin “erdoes_gallai”, joka ratkaisee, täyttääkö jakso Erdös-Gallain lauseen. Ensin tarkistetaan, onko jakson alkioiden summa pariton. Jos näin on, funktio palauttaa False, koska Erdös-Gallain lause ei voi enää täyttyä. Tämän jälkeen tarkistetaan staattisella metodilla is_degree_sequence, onko syötetty sarja astesarja, eli ovatko sarjan elementit ei-lisäytyviä. Tämä on tavallaan turhaa, koska syötteen on tarkoitus olla astejono, joten voit tehokkuuden vuoksi jättää tämän tarkistuksen pois. Tarkistetaan nyt toisen if-lauseen rungossa, täyttyykö lauseen epäyhtälö:

Versio ilman turhaa astejonotestiä:

Graafin tiheys

Graafin tiheys määritellään tietyn graafin särmien lukumäärän ja sen särmien kokonaismäärän suhteena, joka graafilla voisi olla. Toisin sanoen: Se mittaa, kuinka lähellä tietty graafi on täydellistä graafia.
Maksimitiheys on 1, jos graafi on täydellinen. Tämä on selvää, koska graafin särmien maksimimäärä riippuu kärkipisteistä ja se voidaan laskea seuraavasti:
särmien maksimimäärä = ½ * |V| * ( |V| – 1 ).
Toisaalta minimitiheys on 0, jos graafissa ei ole yhtään reunaa, eli se on eristetty graafi.
Ohjaamattomille yksinkertaisille graafeille graafin tiheys määritellään seuraavasti: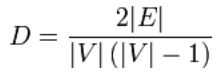

Tiheä graafi on graafi, jossa reunojen lukumäärä on lähellä reunojen maksimimäärää. Graafia, jossa on vain muutama särmä, kutsutaan harvaksi graafiksi. Määritelmä näille kahdelle termille ei ole kovin terävä, eli ei ole olemassa pienintä ylärajaa (supremum) harvalle tiheälle eikä suurinta alarajaa (infimum) tiheän graafin määrittelyyn.
Tarkimmassa matemaattisessa merkintätavassa käytetään ison O:n merkintätapaa:
Tiheä graafi:
Tiheä graafi:
Tiheä graafi on graafi G = (V, E), jossa |E| = Θ(|V|2).
“density” on luokkamme metodi graafin tiheyden laskemiseen:

 def density(self): """ method to calculate the density of a graph """ g = self.__graph_dict V = len(g.keys()) E = len(self.edges()) return 2.0 * E / (V *(V - 1))

Voidaan testata tätä metodia seuraavalla skriptillä. Täydellisen graafin tiheys on 1 ja eristetyn graafin tiheys on 0, kuten näemme edellisen testiskriptin tuloksista:

$ python test_density.py 0.4666666666671.00.0

Kytketty graafi

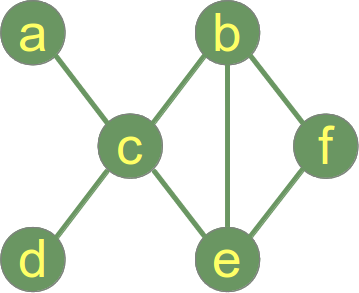Graafin sanotaan olevan kytketty, jos jokainen graafin kärkipari on kytketty. Oikeanpuoleinen esimerkkigraafi on kytketty graafi.
Voidaan yksinkertaisella algoritmilla määrittää, onko graafi kytketty:

1. Valitaan graafin G mielivaltainen solmu x lähtökohdaksi
2. Määritetään kaikkien niiden solmujen joukko A, joihin pääsee x:stä.
3. Jos A on yhtä suuri kuin G:n solmujen joukko, graafi on kytkeytynyt, muuten se on kytkeytymätön.

Toteutamme metodin is_connected tarkistamaan, onko graafi kytkeytynyt graafi. Emme painota tehokkuutta vaan luettavuutta.
Jos lisäämme tämän metodin graafiluokkaamme, voimme testata sitä seuraavalla skriptillä. Olettaen, että tallennat graph-luokan nimellä graph2.py:
Kytketty komponentti on G:n maksimaalinen kytketty aligrafi. Jokainen huippu kuuluu täsmälleen yhteen kytkettyyn komponenttiin, samoin jokainen reuna.

Graafin etäisyys ja halkaisija

Graafin kahden kärkipisteen välinen etäisyys “dist” on näiden kärkipisteiden välisen lyhimmän polun pituus. Etäisyyttä laskettaessa ei sallita takapolkuja, kiertoteitä tai silmukoita.

Oikealla olevassa esimerkkigraafissamme etäisyys kärkipisteen a ja kärkipisteen f välillä on 3, eli dist(a,f) = 3, koska lyhin tie kulkee kärkipisteiden c ja e (tai vaihtoehtoisesti c ja b) kautta.
Graafin g pisteen s eksentrisyys on maksimietäisyys kaikista muista graafin pisteistä:
e(s) = max( { dist(s,v) | v ∈ V })
(V on g:n kaikkien kärkien joukko)
Graafin halkaisija d määritellään graafin minkä tahansa kärkipisteen maksimieksentrisyytenä. Tämä tarkoittaa, että halkaisija on lyhimmän polun pituus etäisimpien solmujen välillä. Graafin halkaisijan määrittämiseksi etsitään ensin lyhin polku kunkin kärkiparin välillä. Minkä tahansa näistä poluista suurin pituus on graafin halkaisija.
Esimerkkigraafistamme näemme suoraan, että halkaisija on 3, koska a:n ja f:n välinen pienin pituus on 3 eikä ole yhtään muuta kärkiparia, jonka polku olisi pidempi.
Seuraavassa menetelmässä toteutetaan algoritmi halkaisijan laskemiseen. Voimme laskea esimerkkigraafimme halkaisijan seuraavalla skriptillä, olettaen jälleen, että täydellinen graafiluokkamme on tallennettu nimellä graph2.py:

from graph2 import Graphg = { "a" : , "b" : , "c" : , "d" : , "e" : , "f" : }graph = Graph(g)diameter = graph.diameter()print(diameter)

Se tulostaa arvon 3.

Kokonaisvaltainen Python-graafiluokka

Oheisesta Python-koodista löydät täydellisen Python-luokkamoduulin kaikkine käsiteltyine metodeineen:graph2.py

Puu/Metsä

Puu (tree / forestPuu (tree)) on suuntaamaton graafi (undirected graph), joka ei sisällä syklejä. Tämä tarkoittaa, että kaikki graafin kaksi kärkeä ovat yhteydessä toisiinsa täsmälleen yhden yksinkertaisen polun kautta.
Metsä on puiden disjointti unioni. Toisin kuin luonnossa esiintyvät metsät, graafiteoriassa metsä voi koostua yhdestä ainoasta puusta!
Graafi, jossa on yksi huippu ja jossa ei ole yhtään särmää, on puu (ja metsä).
Esimerkki puusta: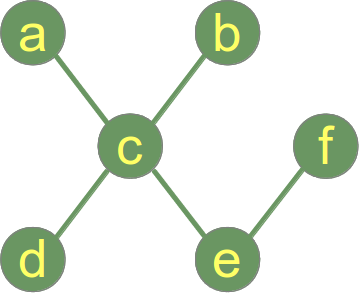

Vaikka edellinen esimerkki kuvaa graafia, joka on puu ja metsä, niin seuraavassa kuvassa on graafi, joka koostuu kahdesta puusta, i.eli graafi on metsä mutta ei puu:

Yleiskuva metsistä:

Metsägraafit, joissa on yksi huippu:

Metsägraafit, joissa on kaksi huippua:

Metsägraafeja, joissa on kolme kärkeä:

Ympäryspuu

Yhteenkytketyn, suuntaamattoman graafin G ylityspuu T on G:n osa-graafi G’, joka on puu,ja G’ sisältää kaikki G:n kärkipisteet ja osajoukon G:n särmiä. G’ sisältää kaikki G:n särmät, jos G on puugraafi. Epävirallisesti G:n jännevä puu on valikoima G:n reunoja, jotka muodostavat puun, joka ulottuu jokaiseen kärkeen. Toisin sanoen jokainen huippu sijaitsee puussa, mutta siinä ei ole syklejä (tai silmukoita).
Esimerkki:
Täysin kytkeytynyt graafi: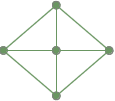

Kaksi jänneverkkopuuta edellisestä täysin kytkeytyneestä graafista: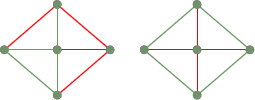

Hamilton-peli

Hamilton-polku on suuntaamattoman tai suunnatun graafin polku, joka käy jokaisessa pisteessä tasan kerran. Hamiltonilainen sykli (tai piiri) on Hamiltonilainen polku, joka on sykli.
Huomautus tietojenkäsittelytieteilijöille: Yleensä ei ole mahdollista määrittää, onko tällaisia polkuja tai syklejä olemassa mielivaltaisissa graafeissa, koska Hamilton-polkuongelma on todistetusti NP-täydellinen.
On nimetty William Rowan Hamiltonin mukaan, joka keksi niin sanotun “icosian-pelin” eli Hamiltonin palapelin, jossa on kyse Hamiltonin syklin löytämisestä dodekaedrin reunagraafista. Hamilton ratkaisi tämän ongelman ikonilaskennan avulla, joka on ykkösen juuriin perustuva algebrallinen rakenne, jolla on monia yhtäläisyyksiä kvaternionien kanssa, jotka hän myös keksi.

Graafi-luokan täydellinen listaus

Voimme testata tätä Graafi-luokkaa seuraavalla ohjelmalla:Jos käynnistämme tämän ohjelman, saamme seuraavan tulosteen:
Footnotes:
1 Graafiteoriassa (ja Python-oppaamme tässä luvussa) tutkittuja graafeja ei pidä sekoittaa funktioiden graafeihin
2 Singleton on joukko, joka sisältää täsmälleen yhden alkion.
Credits:
Narayana Chikkam, nchikkam(at)gmail(dot)com, huomautti indeksivirheestä metodissa “erdoes_gallai”. Kiitos paljon, Narayana!