6.3 Uskomusverkot
Edullisen riippumattomuuden käsitettä voidaan käyttää monien alojen ytimekkääseen esittämiseen. Ajatuksena on, että kun annetaan satunnainen muuttuja X, voi olla olemassa pieni joukko muuttujia, jotkavaikuttavat suoraan muuttujan arvoon siinä mielessä, että X on ehdollisesti riippumaton muista muuttujista, kun suoraan vaikuttavien muuttujien arvot on annettu. Paikallisesti vaikuttavien muuttujien joukkoa kutsutaan Markovin peitoksi. Tätä paikallisuutta hyödynnetään uskomusverkossa. Uskomusverkko on suunnattu malli satunnaismuuttujajoukon ehdollisesta riippuvuudesta. Uskomusverkon ehdollisen riippumattomuuden tarkka toteaminen ottaa huomioon suuntautuneisuuden.
Uskomusverkon määrittelemiseksi aloitetaan joukosta satunnaismuuttujia, jotka edustavat kaikkia mallin ominaisuuksia. Oletetaan, että nämä muuttujat ovat {X1,…,Xn}.Seuraavaksi valitaan muuttujien kokonaisjärjestys, X1,…,Xn.
Ketjusääntö (Proposition 6.3) osoittaa, miten konjunktio hajotetaan ehdollisiin todennäköisyyksiin:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∧ ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
Vai satunnaismuuttujien ja todennäköisyysjakaumien kannalta,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Määritellään satunnaismuuttujan Xi vanhemmat, kirjoitetaanparents(Xi), aminimaaliseksi joukoksi Xi:n edeltäjiä kokonaisjärjestyksessä siten, että muut Xi:n edeltäjät ovat ehdollisesti riippumattomia Xi:stä givenparents(Xi). Eli parents(Xi) ⊆{X1,…,Xi-1} siten, että
P(Xi|Xi-1…X1) = P(Xi|parents(Xi)).
Jos on olemassa useampi kuin yksi minimaalinen joukko, mikä tahansa minimaalinen joukko voidaan valita vanhemmiksi. Minimijoukkoja voi olla useampi kuin yksi vain silloin, kun jotkut edeltäjät ovat deterministisiä funktioita toisista.
Voidaan yhdistää ketjusääntö ja vanhempien määritelmä,jolloin saadaan
P(X1, X2,—, Xn) = ∏i=1n P(Xi|vanhemmat(Xi)).
Todennäköisyyttä kaikkien muuttujien yli, P(X1, X2,—,Xn), kutsutaan yhteiseksi todennäköisyysjakaumaksi. Abelief network määrittelee yhteisentodennäköisyysjakaumanfaktorisoinnin, jossa ehdolliset todennäköisyydetmuodostavat tekijöitä, jotka kerrotaan keskenään.
A belief network, jota kutsutaan myös Bayesiannetworkiksi, on asyklinensuuntautunut graafi (DAG), jossa solmut ovat satunnaismuuttujia. Uskomusverkkoon liittyy joukko ehdollisia todennäköisyysjakaumia – kunkin muuttujan ehdollinen todennäköisyys, kun otetaan huomioon sen vanhemmat (joka sisältää niiden muuttujien ennakkotodennäköisyydet, joilla ei ole vanhempia).
Siten uskomusverkko koostuu
- DAG:sta, jossa jokainen solmu on merkitty satunnaismuuttujalla;
- alueesta jokaiselle satunnaismuuttujalle; ja
- joukosta ehdollisia todennäköisyysjakaumia, jotka antavat P(X|vanhemmat(X)) jokaiselle muuttujalle X.
Hyvin uskomusverkko on rakenteensa puolesta syklinen. Tapa, jolla ketjuverkko muodostaa konjunktion, antaajärjestyksen. Muuttujalla voi olla vanhempina vain edeltäjiä.Erilaiset purkutavat voivat johtaa erilaisiin uskomusverkkoihin.
Asetetaan, että käytämme seuraavia muuttujia, jotka kaikki ovat Boolen-muuttujia, seuraavassa järjestyksessä:
- Tampering on tosi, kun hälyttimeen on tehty peukalointia.
- Tulipalo on tosi, kun on tulipalo.
- Hälytys on tosi, kun hälytys soi.
- Savu on tosi, kun on savua.
- Poistuminen on tosi, jos rakennuksesta poistuu monta ihmistä kerralla.
- Raportti on tosi, jos joku on antanut raportin ihmisten poistumisesta. Raportti on epätosi, jos poistumisesta ei ole raporttia.
Muuttuja Raportti tarkoittaa anturin raporttia siitä, että ihmiset lähtevät. Tämä tieto on epäluotettava, koska tällaisen raportin antaja voi olla pilaileva henkilö, tai kukaan, joka olisi voinut antaa tällaisen raportin, ei ehkä ole ollut tarkkana. Tämä muuttuja on otettu käyttöön, jotta epäluotettavia anturitietoja voidaan käyttää ehdollistamiseen. Agentti tietää, mitä sensori raportoi,mutta sillä on vain epäluotettavia todisteita rakennuksesta poistuvista ihmisistä.Oletetaan osana toimialuetta seuraavat ehdolliset riippumattomuudet:
- Tulipalo on ehdollisesti riippumaton Tamperoinnista (kun ei anneta muuta tietoa).
- Hälytys riippuu sekä tulipalosta että Tamperoinnista. Toisin sanoen emme tee riippumattomuusoletuksia siitä, miten Hälytys riippuu edeltäjistään, kun otetaan huomioon tämä muuttujajärjestys.
- Savu riippuu vain Tulipalosta ja on ehdollisesti riippumaton Tamperoinnista jaHälytyksestä, kun otetaan huomioon, onko Tulipalo.
- Poistuminen riippuu vain Hälytyksestä eikä suoraan Tulipalosta taiTamperoinnista tai Savusta. Toisin sanoen Poistuminen on ehdollisesti riippumaton muista muuttujista, kun otetaan huomioon Hälytys.
- Raportti riippuu vain suoraan Poistumisesta.
Kuvan 6.1 uskomusverkko ilmaisee nämä riippuvuudet.
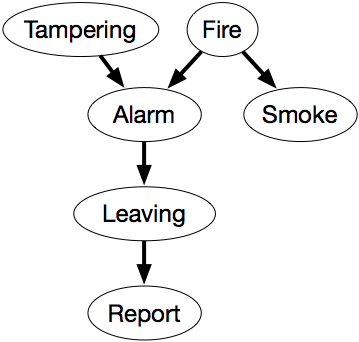
Tämä verkko edustaa faktorointia
P(Tampering,Fire,Alarm,Smoke,Leaving,Raportti) = P(Tamperointi) ×P(Tulipalo) ×P(Hälytys|Tamperointi,Tulipalo) ×P(Savu|Tulipalo) ×P(Poistuminen|Hälytys) ×P(Raportti|Lähdön).
Meidän on myös määriteltävä kunkin muuttujan alue. Oletetaan, että muuttujat ovat Boolean-muuttujia; eli niillä on toimialue {true,false}. Käytämme muuttujan pienellä alkukirjaimella kirjoitettua muunnosta kuvaamaan tosiarvoa ja negaatiota väärästä arvosta. Näin esimerkiksi Tampering=true kirjoitetaan nimellä tampering ja Tampering=false kirjoitetaan nimellä ¬tampering.
Seuraavissa esimerkeissä oletetaan seuraavat ehdolliset todennäköisyydet:
P(palo) = 0.01
P(hälytys | palo ∧ peukalointi) = 0.5
P(hälytys | tulipalo ∧¬tampering) = 0.99
P(hälytys | ¬palo ∧tampering) = 0.85
P(hälytys | ¬palo ∧¬tampering) = 0.0001
P(savu | tulipalo ) = 0.9
P(savu | ¬palo ) = 0.01
P(poistuminen | hälytys) = 0.88
P(poistuminen | ¬hälytys ) = 0.001
P(raportti | poistuminen ) = 0.75
P(raportti | ¬poistuminen ) = 0.01
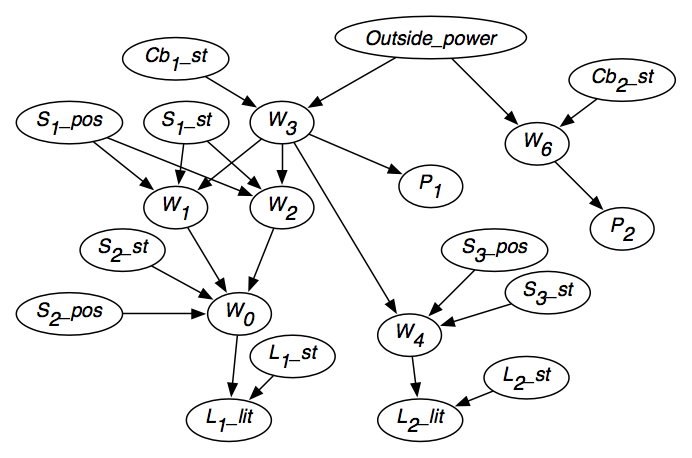
- Kullekin johdolle wi on olemassa satunnaismuuttuja Wi, jonka toimialue on {elävä,kuollut} ja joka ilmaisee, onko johdossa wi virta. Wi=live tarkoittaa, että johdossa wi on virtaa. Wi=kuollut tarkoittaa, että johdossa wi ei ole virtaa.
- Outside_power, jonka toimialue on {live,dead}, ilmaisee, tuleeko rakennukseen virtaa.
- Jokaisen kytkimen si kohdalla muuttuja Si_pos ilmaisee sen sijainnin. Sen toimialue on {ylös,alas}.
- Kunkin kytkimen si osalta muuttuja Si_st tarkoittaa kytkimen si tilaa. Sillä on alue {ok,ylösalaisin,lyhyt,katkonainen,rikki}. Si_st=ok tarkoittaa, että kytkin si toimii normaalisti. Si_st=upside_down tarkoittaa, että kytkinsi on asennettu ylösalaisin. Si_st=lyhyt tarkoittaa, että kytkin si on lyhentynyt ja toimii johtimena. Si_st=rikki tarkoittaa, että kytkin si on rikki eikä anna sähkön virrata.
- Jokaisen katkaisijan Cbi osalta muuttujalla Cbi_st on alue {on,off}. Cbi_st=on tarkoittaa, että cbi:n läpi voi kulkea sähköä ja Cbi_st=off tarkoittaa, että cbi:n läpi ei voi kulkea sähköä.
- Kunkin valaisimen li osalta muuttuja Li_st, jolla on toimialue {ok,katkonainen,rikki}, tarkoittaa valon tilaa. Li_st=ok tarkoittaa, että valo li syttyy, jos siihen kytketään virtaa, Li_st=intermittent tarkoittaa, että valo li syttyy ajoittain, jos siihen kytketään virtaa, ja Li_st=broken tarkoittaa, että valo li ei toimi.
Valitaan järjestys, jossa muuttujan syyt ovatjärjestyksessä ennen muuttujaa. Esimerkiksi muuttuja, joka kertoo, syttyykö valo, tulee muuttujien jälkeen, jotka kertovat, toimiiko valo ja tuleeko valoon virtaa.
Syttyykö valo l1, riippuu vain siitä, onko johdossa w0 virtaa ja toimiiko valo l1 oikein. Muut muuttujat, kuten kytkimen s1 asento, syttyykö valo l2 tai kuka on Kanadan kuningatar, eivät ole merkityksellisiä. Näin ollen L1_litin vanhemmat ovat W0 ja L1_st.
Tarkastellaan muuttujaa W0, joka ilmaisee, onko johdossa w0 virtaa. Jos tietäisimme, onko johdoissa w1 jaw2 virtaa, ja tietäisimme kytkimen s2 asennon ja tietäisimme, toimiiko kytkin oikein, muiden muuttujien (muiden kuinL1_lit) arvo ei vaikuttaisi uskomukseemme siitä, onko johdossa w0 virtaa. Näin ollen W0:n vanhempien tulisi olla S2_Pos, S2_st,W1 ja W2.
Kuvassa 6.2 on esitetty tuloksena saatu uskomusverkko sen jälkeen, kun kunkin muuttujan riippuvuus on otettu huomioon.Uskomusverkko sisältää myös muuttujien toimialueet, kuten kuvassa on esitetty, ja jokaisen muuttujan ehdolliset todennäköisyydet, kun sen vanhemmat on annettu.
Muuttujalle W1 on määritettävä seuraavat ehdolliset todennäköisyydet:
P(W1=elävä|S1_pos=up ∧S1_st=ok ∧W3=elävä)
P(W1=elävä|S1_pos=up ∧S1_st=ok. ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=elävä|S1_pos=alas ∧S1_st=murtunut ∧W3=kuollut).
S1_pos:lle on kaksi arvoa, S1_ok:lle viisi arvoa ja W3:lle kaksi arvoa, joten on olemassa 2×5 ×2 = 20 erilaista tapausta, joissa on määriteltävä arvo arvolle W1=elävä. Todennäköisyysteorian mukaan todennäköisyys W1=elävä näissä 20 tapauksessa voidaan määrittää mielivaltaisesti. Tietenkin alan tuntemus rajoittaa sitä, mitkä arvot ovat järkeviä. Arvot W1=kuollut voidaan laskea arvoista W1=elävä jokaiselle näistä tapauksista.
Koska muuttujalla S1_st ei ole vanhempia, se tarvitsee aiemman jakauman, joka voidaan määrittää todennäköisyyksinä kaikille paitsi yhdelle arvolle; jäljelle jäävä arvo voidaan johtaa rajoituksesta, jonka mukaan kaikkien todennäköisyyksien summa on 1. S1_st:n jakauman määrittämiseksi on siis määritettävä neljä seuraavista viidestä todennäköisyydestä:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
Uskomusverkko on graafinen esitys ehdollisesta riippumattomuudesta.Riippumattomuus mahdollistaa suorien vaikutusten kuvaamisen graafin sisälläja määrää, mitkä todennäköisyydet on määriteltävä. Verkosta voidaan johtaa mielivaltaisia posteriorisia todennäköisyyksiä.
Uskomusverkkoon sulautettu riippumattomuusolettamus on seuraava:Jokainen satunnaismuuttuja on ehdollisesti riippumaton muista kuin jälkeläisistään, kun otetaan huomioon sen vanhemmat. Toisin sanoen, jos X on satunnaismuuttuja, jonka vanhemmat ovat Y1,…, Yn, kaikki satunnaismuuttujat, jotka eivät oleX:n jälkeläisiä, ovat ehdollisesti riippumattomia X:stä, kun otetaan huomioon Y1,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
jos R:ssä ei ole mukana X:n jälkeläisiä. Tätä määritelmää varten sisällytämme X:n itseensä. Tämän yhtälön oikeanpuoleinen puoli on niiden todennäköisyyksien muoto, jotka on määritetty osana uskomusverkostoa.R voi sisältää X:n esivanhempia ja muita solmuja, kunhan ne eivät ole X:n jälkeläisiä.Riippumattomuusolettamus sanoo, että kaikki muiden kuin jälkeläismuuttujien vaikutus otetaan huomioon tietämällä X:n vanhempien arvo.
Usein viittaamme uskomusverkostona vain merkittyyn DAG:iin. Tällöin on tärkeää muistaa, että verkkoon kuuluu myös jokaisen muuttujan toimialue ja joukko ehdollisia todennäköisyysjakaumia.
Kullekin muuttujalle määriteltävien todennäköisyyksien määrä on eksponentiaalinen muuttujan vanhempien määrään nähden.Riippumattomuusolettamus on hyödyllinen sikäli, että toiseen muuttujaan suoraan vaikuttavien muuttujien määrä on pieni. Kannattaa järjestää muuttujat niin, että solmuilla on mahdollisimman vähän vanhempia.
Uskomusverkot ja kausaalisuus
Uskomusverkkoja on usein kutsuttu kausaaliverkoiksi, ja niiden on väitetty olevan hyvä esitys kausaalisuudesta.Muistutetaan, että kausaalimalli ennustaa interventioiden tuloksen.Oletetaan, että sinulla on mielessäsi kausaalimalli jostain toimialueesta, jossa toimialue on määritetty satunnaismuuttujien joukolla. Jos jokaiselle satunnaismuuttujaparille X1ja X2 on olemassa suora kausaalinen yhteys X1:stä X2:een (eli puuttuminen X1:n muuttamiseen jossakin muiden muuttujien yhteydessä vaikuttaa X2:een, eikä tätä voida mallintaa jollakin puuttuvalla muuttujalla), lisää kaari X1:stä X2:een. Odotat, että kausaalimalli noudattaisi uskomusverkon riippumattomuusoletusta. Näin ollen kaikki uskomusverkon johtopäätökset olisivat päteviä.
Odottaisit myös, että tällainen kuvaaja olisi asyklinen; et halua, että jokin aiheuttaa lopulta itsensä. Tämä oletus on järkevä, jos ajatellaan, että satunnaismuuttujat edustavat pikemminkin tiettyjä tapahtumia kuin tapahtumatyyppejä. Tarkastellaan esimerkiksi kausaaliketjua, jonka mukaan “stressaantuneena oleminen” aiheuttaa sen, että “työskentelet tehottomasti”, mikä puolestaan aiheuttaa sen, että “olet stressaantunut”. Näennäisen kierteen katkaisemiseksi voimme esittää “stressaantumisen” eri vaiheissa eri satunnaismuuttujina, jotka viittaavat eri ajankohtiin. Stressaantuminen menneisyydessä aiheuttaa sen, että työskentelet huonosti tällä hetkellä, mikä aiheuttaa sen, että olet stressaantunut tulevaisuudessa. Muuttujien olisi täytettävä selkeysperiaate ja niillä olisi oltava hyvin määritelty merkitys. Muuttujia ei pitäisi nähdä tapahtumatyyppeinä.
Uskomusverkolla itsellään ei ole mitään sanottavaa kausaalisuudesta, ja se voi edustaa ei-kausaalista riippumattomuutta, mutta se vaikuttaa erityisen sopivalta silloin, kun alueella on kausaalisuutta. Paikallista kausaliteettia edustavien kaarien lisääminen tuottaa yleensä pienen uskomusverkon. Kuvan 6.2 uskomusverkko osoittaa, miten tämä voidaan tehdä yksinkertaiselle alueelle.
Acausal network models interventions. Jos joku keinotekoisesti pakottaisi muuttujan saamaan tietyn arvon, se vaikuttaisi muuttujan jälkeläisiin – mutta ei muihin solmuihin. Lopuksi voit nähdä, miten uskomusverkkojen kausaalisuus liittyy kohdassa 5.7 käsiteltyyn kausaaliseen ja todisteelliseen päättelyyn. Kausaalinen uskomusverkko voidaan nähdä pois aksiomatisoinnista kausaaliseen suuntaan. Päättely uskomusverkoissavastaa syiden päättelyä ja sittenennustamista niistä. Kohdassa 5.7 käsitellyn logiikkaan perustuvan abduktiivisen näkemyksen ja uskomusverkkojen välillä on suora yhteys: Uskomusverkot voidaan mallintaa logiikkaohjelmina, joissa on todennäköisyyksiä mahdollisten hypoteesien suhteen. Tätä kuvataan kohdassa 14.3.
Huomaa uskomusverkkoon koodatun riippumattomuuden määritelmässä oleva rajoitus “jokainen satunnaismuuttuja on ehdollisesti riippumaton muista kuin jälkeläisistään, kun otetaan huomioon sen vanhemmat”. JosR sisältää muuttujan X jälkeläisen, riippumattomuusoletus ei olesuorasti sovellettavissa.
Muuttujalla S1_pos ei ole vanhempia. Näin ollen uskomusverkkoon sulautettu riippumattomuus määrittelee, että P(S1_pos=päällä|A) =P(S1_pos=päällä) mille tahansa A:lle, johon ei liityS1_posin jälkeläistä. Jos A sisältää S1_pos=up:n jälkeläisen – esimerkiksi jos A on S2_pos=up∧L1_lit=tosi – riippumattomuusolettamusta ei voida suoraan soveltaa.
Tätä verkkoa voidaan käyttää monin tavoin:
- Valmistamalla ehdollistamalla tiedon siitä, että katkaisijat ja kytkimet ovat kunnossa, sekä ulkoisen tehon ja katkaisijoiden asennon arvot, tämä verkko voi simuloida, miten valaistuksen pitäisi toimia.
- Verkko voi päätellä minkä tahansa lopputuloksen todennäköisyyden – esimerkiksi kuinka todennäköistä on, että l1 syttyy.
- Kytkimien arvot ja se, syttyvätkö valot,voidaan päätellä posteriorinen todennäköisyys sille, että kukin kytkin tai katkaisija on jossakin tietyssä tilassa.
- Joidenkin havaintojen perusteella verkkoa voidaan käyttää päättelemään taaksepäin kytkimien todennäköisimmän asennon määrittämiseksi.
- Joidenkin kytkimien asentojen, joidenkin ulostulojen ja joidenkin väliarvojen perusteella verkkoa voidaan käyttää minkä tahansa muun verkon muuttujan todennäköisyyden määrittämiseen.
Uskomusverkko määrittelee yhteisen todennäköisyysjakauman, josta voidaan johtaa mielivaltaisia ehdollisia todennäköisyyksiä. Verkkoa voidaan kysyä kysymällä minkä tahansa muuttujan ehdollista todennäköisyyttä, joka riippuu minkä tahansa muun muuttujan arvoista. Tämä tehdään tyypillisesti antamalla havaintoja joistakin muuttujista ja kysymällä jotain toista muuttujaa.
P(tulipalo) = 0.01
P(ilmoitus ) = 0.028
P(savu) = 0.0189
Raportin tarkkailu antaa seuraavan tuloksen:
P(tulipalo |raportti)= 0.2305
P(savu |raportti) = 0.215
Odotetusti sekä peukaloinnin että tulipalon todennäköisyys kasvaa raportin myötä. Koska tulipalo lisääntyy, myös savun todennäköisyys kasvaa.
Esitettäisiin sen sijaan, että savua olisi havaittu:
P(tulipalo|savu) = 0.476
P(raportti |savu) = 0.320
Huomaa, että savun havaitseminen ei vaikuta peukaloinnin todennäköisyyteen; raportin ja tulipalon todennäköisyydet kuitenkin kasvavat.
Esitetään, että sekä raportti että savu havaittiin:
P(tulipalo |raportti ∧ savu) = 0.964
Kummankin havainnointi tekee tulipalosta vielä todennäköisemmän. Raportin yhteydessä savun läsnäolo tekee kuitenkin peukaloinnin epätodennäköisemmäksi. Tämä johtuu siitä, että raportti selittyy tulipalolla, joka on nyt todennäköisempi.
Emme sen sijaan oleta, että raportti, mutta ei savua, havaittiin:
P(tulipalo|raportti ∧¬savu) = 0.0294
Raportin yhteydessä tulipalo muuttuu paljon epätodennäköisemmäksi ja näin ollen peukaloinnin todennäköisyys kasvaa selittämään raporttia.
Tämä esimerkki havainnollistaa, kuinka uskomusverkonriippumattomuusolettamus antaa tervejärkisiä johtopäätöksiä ja havainnollistaa myös, kuinka selittäminen pois on seurausta uskomusverkon riippumattomuusolettamasta.
- 6.3.1 Uskomusverkkojen rakentaminen