Tetraedri

Tämän sivun sisältö Mikä on tetraedri? Tetraedrin osat Tetraedrin luvut Tetraedri kuutiossa Tetraedrin renkaat Tetraedrit internetissä

Pääsivulle “Matemaattiset basteet”

Mikä on tetraedri?

Tetraedri on kolmiulotteinen hahmo, jossa on neljä yhtäpitävää kolmiota. Jos nostat kolme kolmiota ylös (1), saat tetraedrin ylhäältä katsottuna (2). Yleensä se esitetään perspektiivinä (3).

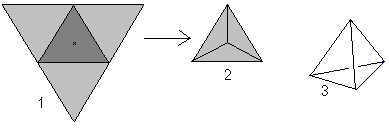
Jos tarkastellaan sanaa tetraedri (tetraedri tarkoittaa “jossa on neljä tasoa”), tetraedriksi voidaan kutsua jokaista pyramidia, jonka pohjana on kolmio.

Tetraedri on kuitenkin tällä sivustolla suora, säännöllinen kolmiopyramidi.

Tetraedrin osat
Sivukolmion korkeus ja pinta-ala
Neljä tasasivuista kolmiota muodostaa tetraedrin.

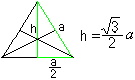…	Poimitaan yksi kolmio: Kolme korkeutta leikkaavat toisensa yhdessä pisteessä kuten jokaisessa kolmiossa. Tämä on kolmion keskipiste. Korkeus voidaan laskea sivun a mukaan seuraavasti: h=sqr(3)/2*a Pythagoraan lauseen avulla.

Korkeudet ovat myös keskipisteitä ja leikkaavat toisensa suhteessa2:1. Tätä käytetään seuraavissa laskelmissa.

Kolmion pinta-ala on A=sqr(3)/4*a².

Avaruuskorkeus

Tetraedrin korkeus on peruskolmion keskipisteen (1) ja kärkipisteen (2) välillä. Laskelmissa otetaan huomioon ns. tukikolmio (3, keltainen), joka muodostuu yhdestä reunasta ja kahdesta kolmion korkeudesta. Siellä on H=sqr(6)/3*a Pythagoraan lauseen avulla.
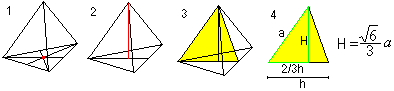
Keskipiste, ympyröity pallo ja ympyröity pallo Tetraedrin keskipiste on kahden avaruuskorkeuden (1,2,3) leikkauspiste. Se on painopiste, pallon keskipiste neljän kulman kautta ja suurimman pallon keskipiste, joka vielä mahtuu tetraedrin sisälle (4).

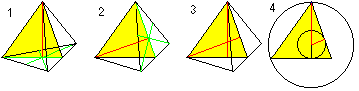
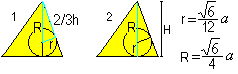….	Saat kaksi kaavaa r:lle ja R:lle Pythagoraan lauseen (1) ja H=R+r:n (2) avulla: On r=sqr(6)/12*a , R=sqr(6)/4*a.

Kulmapinta

….…..

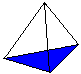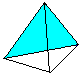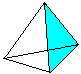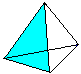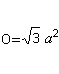Pohjan ja sivupintojen pinta-ala muodostaa pinnanO. On O=4*A (kolmio) = sqr(3)a².

Tilavuus

Tetraediset luvut ylhäältä

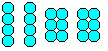…….	Jos liimaat 20 kuulaa kahteen ryhmään neljällä ja kahteen kuudella, saat tunnetun arvoituksen: Sinun on muodostettava pyramidi, jossa on neljä kappaletta.

Vastaavia arvoituksia on monia.

Tetraedri kuutiossa ylhäällä
Kuusi kasvojen lävistäjää muodostavat kuutiossa tetraedrin.
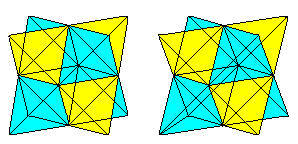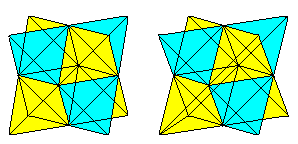
Jos osaat 3D-näkemyksen, voit kolmiulotteisesti tarkastella seuraavia kahta kuutioparia.

Tetraedrin tilavuus on kolmasosa kuution tilavuudesta.

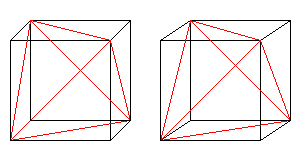
Jos piirrät toisen tetraedrin ja leikkausviivat,saat kahden tetraedrin läpileikkauksen.

Hahmo muodostuu alkuperäisen kuution kasvojen lävistäjistä ja sivuneliöiden keskipisteiden yhdysviivoista. Viimeiset kivet muodostavat oktaedrin.

Tetraedreistä muodostetut renkaat alkuun
Voit tehdä paperitetraedrejä ja liimata niistä parillisen määrän renkaaseen. Rengas voi jatkuvasti kiertyä sisäänpäin tai ulospäin keskeltä. Tämä on kaunis lelu. – Näitä renkaita kutsutaan myös kaleidosykleiksi.löydät lisää sivuiltani Kaleidosyklit.

Tetraedritonternettop

Saksa

Christof Weber
Was tämä Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)

Albert Kluge
Einrotierender Tetraeder als Java-Applet

FAZ
Tetraederpackung:Eins geht noch

Georg Burkhard
Pyramidedes Cestius, Rom (u.a.)

Gerd Müller
PlatonischeKörper in Stereodarstellung

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder

LANDRAT-LUCAS-GYMNASIUM Leverkusen
SierpinskiTetraeder

ruhr-guide
TetraederBottrop

Wikipedia
Tetraeder,Tetraeder (Bottrop),Tetrapode, Tetraederzahl

Finnish

Eric W. Weisstein (World of Mathematics)
Tetraedri

H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraedri

Joyce Frost ja Peg Cagle (mathforum)
Hämmästyttävä, tilantäyteinen, epäsäännöllinen tetraedri

Wikipedia
Tetraedri
Tetraedri
Tetraedri,Tetraedri(rakenne), Tetrapod(rakenne), tetraedrinluku

>Tetraederin lukumäärä

>Tetraedrin rakenne