Christian Bohr et le concept de liaison coopérativeEdit
En 1904, Christian Bohr a étudié la liaison de l’hémoglobine à l’oxygène dans différentes conditions. En traçant la saturation de l’hémoglobine en oxygène en fonction de la pression partielle de l’oxygène, il a obtenu une courbe sigmoïdale (ou “en forme de S”). Cela indique que plus l’oxygène est lié à l’hémoglobine, plus il est facile pour l’oxygène de se lier – jusqu’à ce que tous les sites de liaison soient saturés. En outre, Bohr a remarqué que l’augmentation de la pression de CO2 déplaçait cette courbe vers la droite – c’est-à-dire que des concentrations plus élevées de CO2 rendent plus difficile la liaison de l’oxygène à l’hémoglobine. Ce dernier phénomène, ainsi que l’observation que l’affinité de l’hémoglobine pour l’oxygène augmente avec l’augmentation du pH, est connu sous le nom d’effet Bohr.

On dit d’une molécule réceptrice qu’elle présente une liaison coopérative si sa liaison au ligand évolue de façon non linéaire avec la concentration du ligand. La coopérativité peut être positive (si la liaison d’une molécule de ligand augmente l’affinité apparente du récepteur, et donc augmente les chances de liaison d’une autre molécule de ligand) ou négative (si la liaison d’une molécule de ligand diminue l’affinité et donc rend moins probable la liaison d’autres molécules de ligand). L'”occupation fractionnelle” Y ¯ {\displaystyle {\bar {Y}}}

d’un récepteur avec un ligand donné est définie comme la quantité de sites de liaison liés au ligand divisée par la quantité totale de sites de liaison du ligand : Y ¯ = + = {\displaystyle {\bar {Y}}={\frac {}{+}={\frac {}{}}}.

Si Y ¯ = 0 {\displaystyle {\bar {Y}}=0}

, alors la protéine est complètement non liée, et si Y ¯ = 1 {\displaystyle {\bar {Y}}=1}.

, elle est complètement saturée. Si le tracé de Y ¯ {\displaystyle {\bar {Y}}}

à l’équilibre en fonction de la concentration du ligand est de forme sigmoïde, comme observé par Bohr pour l’hémoglobine, cela indique une coopérativité positive. Si ce n’est pas le cas, aucune déclaration ne peut être faite sur la coopérativité en regardant ce seul tracé.
Le concept de liaison coopérative ne s’applique qu’aux molécules ou aux complexes ayant plus d’un site de liaison du ligand. Si plusieurs sites de liaison du ligand existent, mais que la liaison du ligand à l’un des sites n’affecte pas les autres, on dit que le récepteur est non coopératif. La coopérativité peut être homotrope, si un ligand influence la liaison des ligands du même type, ou hétérotrope, s’il influence la liaison d’autres types de ligands. Dans le cas de l’hémoglobine, Bohr a observé une coopérativité positive homotrope (la liaison de l’oxygène facilite la liaison de plus d’oxygène) et une coopérativité négative hétérotrope (la liaison du CO2 réduit la facilité de l’hémoglobine à fixer l’oxygène.)
Tout au long du 20ème siècle, divers cadres ont été développés pour décrire la liaison d’un ligand à une protéine avec plus d’un site de liaison et les effets coopératifs observés dans ce contexte.
L’équation de HillEdit
La première description de la liaison coopérative à une protéine multisite a été développée par A.V. Hill. S’inspirant des observations de la liaison de l’oxygène à l’hémoglobine et de l’idée que la coopérativité provenait de l’agrégation des molécules d’hémoglobine, chacune liant une molécule d’oxygène, Hill a proposé une équation phénoménologique qui porte depuis son nom :
Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\displaystyle {\bar {Y}}={\frac {K\cdot {}^{n}}{1+K\cdot {}^{n}}={\frac {^{n}}{K^{*}+^{n}}={\frac {^{n}}{K_{d}^{n}+^{n}}}}

where n {\displaystyle n}

est le “coefficient de Hill”, {\displaystyle }

représente la concentration du ligand, K {\displaystyle K}

représente une constante d’association apparente (utilisée dans la forme originale de l’équation), K ∗ {\displaystyle K^{*}}

est une constante de dissociation empirique, et K d {\displaystyle K_{d}}

une constante de dissociation microscopique (utilisée dans les formes modernes de l’équation, et équivalente à une E C 50 {\displaystyle \mathrm {EC} _{50}}

). Si n < 1 {\displaystyle n<1}

, le système présente une coopérativité négative, tandis que la coopérativité est positive si n > 1 {\displaystyle n>1}.

. Le nombre total de sites de liaison du ligand est une limite supérieure pour n {\displaystyle n}.

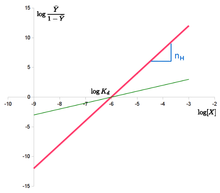
. L’équation de Hill peut être linéarisée comme suit : log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}=n\cdot {}\log-n\cdot {}\log K_{d}}

Le “Hill plot” est obtenu en traçant log Y ¯ 1 – Y ¯ {\displaystyle \log {\frac {\bar {Y}{1-{\bar {Y}}}}}

versus log {\displaystyle \log}

. Dans le cas de l’équation de Hill, il s’agit d’une droite de pente n H {\displaystyle n_{H}}.

et une ordonnée à l’origine log ( K d ) {\displaystyle \log(K_{d})}

. Cela signifie que la coopérativité est supposée être fixe, c’est-à-dire qu’elle ne change pas avec la saturation. Cela signifie également que les sites de liaison présentent toujours la même affinité, et que la coopérativité ne provient pas d’une affinité qui augmente avec la concentration du ligand.
L’équation d’AdairEdit
G.S. Adair a constaté que le tracé de Hill pour l’hémoglobine n’était pas une ligne droite, et a émis l’hypothèse que l’affinité de liaison n’était pas un terme fixe, mais dépendait de la saturation du ligand. Ayant démontré que l’hémoglobine contenait quatre hèmes (et donc des sites de liaison pour l’oxygène), il est parti de l’hypothèse que l’hémoglobine totalement saturée se forme par étapes, avec des formes intermédiaires comportant une, deux ou trois molécules d’oxygène liées. La formation de chaque stade intermédiaire à partir de l’hémoglobine non liée peut être décrite à l’aide d’une constante d’association macroscopique apparente K i {\displaystyle K_{i}}.

. L’occupation fractionnelle qui en résulte peut être exprimée comme suit : Y ¯ = 1 4 ⋅ K I + 2 K I I 2 + 3 K I I I 3 + 4 K I V 4 1 + K I + K I I 2 + K I I I 3 + K I V 4 {\displaystyle {\bar}={{\f{\f{\i}}}. {Y}}={\frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, pour toute protéine avec n sites de liaison au ligand :
Y ¯ = 1 n K I + 2 K I I 2 + … + n K n n 1 + K I + K I I 2 + … + K n n {\displaystyle {\bar {Y}}={\frac {1}{n}{\frac {K_{I}+2K_{II}^{2}+\ldots +nK_{n}^{n}}{1+K_{I}+K_{II}^{2}+\ldots +K_{n}^{n}}}}

où n désigne le nombre de sites de liaison et chaque K i {\displaystyle K_{i}}.

est une constante d’association combinée, décrivant la liaison de i molécules de ligand.En combinant le traitement d’Adair avec le graphe de Hill, on arrive à la définition expérimentale moderne de la coopérativité (Hill, 1985, Abeliovich, 2005). En combinant le traitement d’Adair avec le diagramme de Hill, on obtient la définition expérimentale moderne de la coopérativité (Hill, 1985, Abeliovich, 2005). On peut montrer que le coefficient de Hill résultant, ou plus précisément la pente du diagramme de Hill calculée à partir de l’équation d’Adair, est le rapport entre la variance du nombre de liaisons et la variance du nombre de liaisons dans un système équivalent de sites de liaison sans interaction. Ainsi, le coefficient de Hill définit la coopérativité comme une dépendance statistique d’un site de liaison à l’état du ou des autres sites.
L’équation de KlotzEdit
Travaillant sur les protéines de liaison au calcium, Irving Klotz a déconvolué les constantes d’association d’Adair en considérant la formation par étapes des stades intermédiaires, et a essayé d’exprimer la liaison coopérative en termes de processus élémentaires régis par la loi d’action de masse. Dans son cadre, K 1 {\displaystyle K_{1}}

est la constante d’association régissant la liaison de la première molécule de ligand, K 2 {\displaystyle K_{2}}

la constante d’association régissant la liaison de la deuxième molécule de ligand (une fois que la première est déjà liée), etc. Pour Y ¯ {\displaystyle {\bar {Y}}}

, cela donne : Y ¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 …. K n ) n {\displaystyle {\bar {Y}}={\frac {1}{n}{\frac {K_{1}+2K_{1}K_{2}^{2}+\ldots +n\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Il est intéressant de noter que les constantes K 1 {\displaystyle K_{1}}

, K 2 {\displaystyle K_{2}}

et ainsi de suite ne se rapportent pas à des sites de liaison individuels. Ils décrivent combien de sites de liaison sont occupés, plutôt que lesquels. Cette forme présente l’avantage de reconnaître facilement la coopérativité lorsqu’on examine les constantes d’association. Si tous les sites de liaison du ligand sont identiques avec une constante d’association microscopique K {\displaystyle K}

, on s’attend à ce que K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K {\displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}K,\ldots K_{n}={\frac {1}{n}}K}

(c’est-à-dire K i = n – i + 1 i K {\displaystyle K_{i}={\frac {n-i+1}{i}}K}

) en l’absence de coopérativité. On a une coopérativité positive si K i {\displaystyle K_{i}}

se situe au-dessus de ces valeurs attendues pour i > 1 {\displaystyle i>1}

.
L’équation de Klotz (qui est parfois aussi appelée équation d’Adair-Klotz) est encore souvent utilisée dans la littérature expérimentale pour décrire les mesures de la liaison des ligands en termes de constantes de liaison apparentes séquentielles.
Équation de PaulingEdit
Au milieu du 20e siècle, il y avait un intérêt accru pour les modèles qui ne décriraient pas seulement les courbes de liaison de façon phénoménologique, mais offriraient un mécanisme biochimique sous-jacent. Linus Pauling a réinterprété l’équation fournie par Adair, en supposant que ses constantes étaient la combinaison de la constante de liaison du ligand ( K {\displaystyle K}

dans l’équation ci-dessous) et de l’énergie provenant de l’interaction entre les sous-unités de la protéine coopérative ( α {\displaystyle \alpha }

ci-dessous). Pauling a en fait dérivé plusieurs équations, en fonction du degré d’interaction entre les sous-unités. En se basant sur des hypothèses erronées concernant la localisation des hèmes, il a opté pour la mauvaise pour décrire la fixation de l’oxygène par l’hémoglobine, en supposant que la sous-unité était disposée en carré. L’équation ci-dessous fournit l’équation pour une structure tétraédrique, qui serait plus précise dans le cas de l’hémoglobine : Y ¯ = K + 3 α K 2 2 + 3 α 3 K 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 + 4 α 3 K 3 3 + α 6 K 4 4 {\displaystyle {\bar {Y}}={\frac {K+3\alpha {}K^{2}^{2}+3\alpha {}^{3}K^{3}^{3}+\alpha {}^{6}K^{4}^{4}}{1+4K+6\alpha {}K^{2}^{2}+4\alpha {}^{3}K^{3}^{3}+\alpha {}^{6}K^{4}^{4}}}}

Le modèle KNFEdit
Sur la base de résultats montrant que la structure des protéines coopératives changeait lors de la liaison à leur ligand, Daniel Koshland et ses collègues ont affiné l’explication biochimique du mécanisme décrit par Pauling. Le modèle Koshland-Némethy-Filmer (KNF) suppose que chaque sous-unité peut exister dans l’une des deux conformations suivantes : active ou inactive. La liaison d’un ligand à une sous-unité induirait un changement de conformation immédiat de cette sous-unité de la conformation inactive à la conformation active, un mécanisme décrit comme “ajustement induit”. La coopérativité, selon le modèle KNF, proviendrait des interactions entre les sous-unités, dont la force varie en fonction des conformations relatives des sous-unités impliquées. Pour une structure tétraédrique (ils ont également considéré des structures linéaires et carrées), ils ont proposé la formule suivante :
Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B ( K X K t ) 2 + 3 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {\displaystyle {\barbar}={{\flexible}} {Y}}={\flexible}. {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Where K X {\displaystyle K_{X}}

est la constante d’association pour X, K t {\displaystyle K_{t}}

est le rapport entre les états B et A en l’absence de ligand (“transition”), K A B {\displaystyle K_{AB}}

et K B B {\displaystyle K_{BB}}

sont les stabilités relatives des paires de sous-unités voisines par rapport à une paire où les deux sous-unités sont dans l’état A (Notez que l’article de KNF présente en fait N s {\displaystyle N_{s}}

, le nombre de sites occupés, qui est ici 4 fois Y ¯ {\displaystyle {\bar {Y}}}.

).
Le modèle MWCEdit


Le modèle de Monod-Wyman-Changeux (MWC) pour les transitions allostériques concertées est allé un peu plus loin en explorant la coopérativité à partir de la thermodynamique et des conformations tridimensionnelles. Il a été formulé à l’origine pour des protéines oligomères avec des sous-unités identiques disposées symétriquement, chacune d’entre elles possédant un site de liaison au ligand. Selon ce cadre, deux (ou plusieurs) états conformationnels interconvertibles d’une protéine allostérique coexistent dans un équilibre thermique. Les états – souvent appelés tendu (T) et relaxé (R) – diffèrent en affinité pour la molécule de ligand. Le rapport entre les deux états est régulé par la liaison de molécules de ligand qui stabilisent l’état de plus grande affinité. Fait important, toutes les sous-unités d’une molécule changent d’état en même temps, un phénomène connu sous le nom de “transition concertée”.
La constante d’isomérisation allostérique L décrit l’équilibre entre les deux états lorsqu’aucune molécule de ligand n’est liée : L = {\displaystyle L={\frac {\left}{\left}}.

. Si L est très grand, la majeure partie de la protéine existe à l’état T en l’absence de ligand. Si L est petit (proche de un), l’état R est presque aussi peuplé que l’état T. Le rapport des constantes de dissociation du ligand des états T et R est décrit par la constante c : c = K d R K d T {\displaystyle c={\frac {K_{d}^{R}}{K_{d}^{T}}}}

. Si c = 1 {\displaystyle c=1}

, les deux états R et T ont la même affinité pour le ligand et le ligand n’affecte pas l’isomérisation. La valeur de c indique également dans quelle mesure l’équilibre entre les états T et R change lors de la liaison du ligand : plus c est petit, plus l’équilibre se déplace vers l’état R après une liaison. Avec α = K d R {\displaystyle \alpha ={\frac {}{K_{d}^{R}}}}

, l’occupation fractionnée est décrite comme : Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {Y}}={\frac {\alpha (1+\alpha )^{n-1}+Lc\alpha (1+c\alpha )^{n-1}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Le tracé de Hill sigmoïde des protéines allostériques peut alors être analysé comme une transition progressive de l’état T (faible affinité) à l’état R (forte affinité) lorsque la saturation augmente. La pente du diagramme de Hill dépend également de la saturation, avec une valeur maximale au point d’inflexion. Les intercepts entre les deux asymptotes et l’axe des ordonnées permettent de déterminer les affinités des deux états pour le ligand.

Dans les protéines, le changement de conformation est souvent associé à l’activité, ou à l’activité vers des cibles spécifiques. Cette activité est souvent ce qui est physiologiquement pertinent ou ce qui est mesuré expérimentalement. Le degré de changement de conformation est décrit par la fonction d’état R ¯ {\displaystyle {\bar {R}}}.

, qui désigne la fraction de protéine présente dans le R {\displaystyle R}.

state. Comme l’illustre le diagramme énergétique, R ¯ {\displaystyle {\bar {R}}}

augmente lorsque plus de molécules de ligand se lient. L’expression de R ¯ {\displaystyle {\bar {R}}}

est : R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {R}}={\frac {(1+\alpha )^{n}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Un aspect crucial du modèle MWC est que les courbes pour Y ¯ {\displaystyle {\bar {Y}}}

et R ¯ {\displaystyle {\bar {R}}}.

ne coïncident pas, c’est-à-dire que la saturation fractionnelle n’est pas un indicateur direct de l’état conformationnel (et donc de l’activité). De plus, les degrés de coopérativité de la liaison et de la coopérativité de l’activation peuvent être très différents : un cas extrême est fourni par le moteur des flagelles des bactéries avec un coefficient de Hill de 1,7 pour la liaison et de 10,3 pour l’activation. La supra-linéarité de la réponse est parfois appelée ultrasensibilité.
Si une protéine allostérique se lie à une cible qui a également une affinité plus élevée pour l’état R, alors la liaison de la cible stabilise davantage l’état R, augmentant ainsi l’affinité du ligand. Si, au contraire, une cible se lie préférentiellement à l’état T, la liaison de la cible aura un effet négatif sur l’affinité du ligand. De telles cibles sont appelées modulateurs allostériques.
Depuis sa création, le cadre MWC a été étendu et généralisé. Des variations ont été proposées, par exemple pour prendre en compte les protéines avec plus de deux états, les protéines qui se lient à plusieurs types de ligands ou plusieurs types de modulateurs allostériques et les protéines avec des sous-unités ou des sites de liaison au ligand non identiques.