Christian Bohr és a kooperatív kötődés fogalmaSzerkesztés
1904-ben Christian Bohr a hemoglobin oxigénhez való kötődését vizsgálta különböző körülmények között. Amikor a hemoglobin oxigénnel való telítettségét az oxigén parciális nyomásának függvényében ábrázolta, egy szigmoidális (vagy “S-alakú”) görbét kapott. Ez azt jelzi, hogy minél több oxigén kötődik a hemoglobinhoz, annál könnyebben kötődik még több oxigén – egészen addig, amíg az összes kötőhely telítődik. Ezenkívül Bohr észrevette, hogy a növekvő CO2-nyomás jobbra tolja el ezt a görbét – azaz a magasabb CO2-koncentráció megnehezíti a hemoglobin számára az oxigén megkötését. Ez utóbbi jelenséget, valamint azt a megfigyelést, hogy a hemoglobin oxigénhez való affinitása a pH növekedésével nő, Bohr-effektusként ismerjük.

A receptormolekuláról azt mondjuk, hogy kooperatív kötődést mutat, ha a ligandumhoz való kötődése nem lineárisan skálázódik a ligandum koncentrációjával. A kooperativitás lehet pozitív (ha egy ligandummolekula kötődése növeli a receptor látszólagos affinitását, és így növeli egy másik ligandummolekula kötődésének esélyét) vagy negatív (ha egy ligandummolekula kötődése csökkenti az affinitást, és így más ligandummolekulák kötődését teszi kevésbé valószínűvé). A “frakcionális foglaltság” Y ¯ {\displaystyle {\bar {Y}}}

egy receptornak egy adott ligandummal való foglaltságát úgy határozzuk meg, hogy a ligandumhoz kötött kötőhelyek mennyiségét elosztjuk a ligandumhoz kötött kötőhelyek teljes mennyiségével: Y ¯ = + = {\displaystyle {\bar {Y}}={\frac {}{+}}={\frac {}{}{}}}}}}

Ha Y ¯ = 0 {\displaystyle {\bar {Y}}=0}

, akkor a fehérje teljesen kötetlen, és ha Y ¯ = 1 {\displaystyle {\bar {Y}}=1}

, akkor teljesen telített. Ha az Y ¯ {\displaystyle {\bar {Y}}}

az egyensúlyban a ligandum koncentrációjának függvényében szigmoid alakú, ahogy azt Bohr a hemoglobin esetében megfigyelte, ez pozitív kooperativitásra utal. Ha nem így van, akkor pusztán ennek a grafikonnak a vizsgálatából nem lehet a kooperativitásra vonatkozó kijelentést tenni.
A kooperatív kötődés fogalma csak olyan molekulákra vagy komplexekre vonatkozik, amelyekben egynél több ligandum kötőhelye van. Ha több ligandumkötő hely létezik, de a ligandum bármelyik helyhez való kötődése nem befolyásolja a többit, akkor a receptort nem kooperatívnak mondjuk. A kooperativitás lehet homotróp, ha egy ligandum befolyásolja az azonos típusú ligandumok kötődését, vagy heterotróp, ha más típusú ligandumok kötődését befolyásolja. A hemoglobin esetében Bohr homotróp pozitív kooperativitást (az oxigén megkötése elősegíti több oxigén megkötését) és heterotróp negatív kooperativitást (a CO2 megkötése csökkenti a hemoglobin oxigénmegkötési képességét) figyelt meg.)
A 20. század folyamán különböző keretrendszereket dolgoztak ki egy ligandumnak egynél több kötőhellyel rendelkező fehérjéhez való kötődésének és az ezzel összefüggésben megfigyelt kooperatív hatásoknak a leírására.
A Hill-egyenletSzerkesztés
A több kötőhellyel rendelkező fehérjéhez való kooperatív kötődés első leírását A.V. Hill dolgozta ki. Az oxigén hemoglobinhoz való kötődésének megfigyeléseire és arra az elképzelésre támaszkodva, hogy a kooperativitás a hemoglobinmolekulák aggregációjából ered, amelyek mindegyike egy-egy oxigénmolekulát köt meg, Hill egy fenomenológiai egyenletet javasolt, amelyet azóta róla neveztek el:
Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\displaystyle {\bar {Y}}={\frac {K\cdot {}^{n}}}{1+K\cdot {}^{n}}}={\frac {^{n}}}{K^{*}+^{n}}}={\frac {^{n}}{K_{d}^{n}+^{n}}}}

hol n {\displaystyle n}

a “Hill-koefficiens”, {\displaystyle} {\displaystyle }

a ligandum koncentrációját, K {\displaystyle K}

a látszólagos asszociációs állandó (az egyenlet eredeti formájában használt), K ∗ {\displaystyle K^{*}}}

egy empirikus disszociációs állandó, és K d {\displaystyle K_{d}}

egy mikroszkopikus disszociációs állandó (az egyenlet modern formáiban használt, és E C 50 {\displaystyle \mathrm {EC} _{50}}

). Ha n < 1 {\displaystyle n<1}

, a rendszer negatív kooperativitást mutat, míg a kooperativitás pozitív, ha n > 1 {\displaystyle n>1}

. A ligandumkötő helyek teljes száma felső korlátot jelent az n {\displaystyle n}

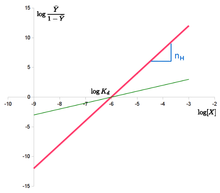
. A Hill-egyenlet a következőképpen linearizálható: log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {\displaystyle \log {\frac {\bar {\bar {Y}}{1-{\bar {Y}}}}=n\cdot {}\log-n\cdot {}\log K_{d}}

A “Hill plot” a log Y ¯ 1 – Y ¯ {\displaystyle \log {\frac {\bar {\bar {Y}}}{1-{\bar {Y}}}}}

a log {\displaystyle \log} ellenében.

. A Hill-egyenlet esetében ez egy egyenes, amelynek meredeksége n H {\displaystyle n_{H}}

és metszéspont log ( K d ) {\displaystyle \log(K_{d})}

. Ez azt jelenti, hogy a kooperativitást fixnek feltételezzük, azaz nem változik a telítettséggel. Ez azt is jelenti, hogy a kötőhelyek mindig azonos affinitást mutatnak, és a kooperativitás nem a ligandum koncentrációjával növekvő affinitásból ered.
Az Adair-egyenletSzerkesztés
G.S. Adair azt találta, hogy a hemoglobin Hill-diagramja nem egyenes, és feltételezte, hogy a kötési affinitás nem egy rögzített kifejezés, hanem a ligandum telítettségétől függ. Miután kimutatta, hogy a hemoglobin négy hemet (és így kötőhelyet az oxigén számára) tartalmaz, abból a feltételezésből indult ki, hogy a teljesen telített hemoglobin fokozatosan alakul ki, és közbenső formái egy, két vagy három oxigénmolekulát tartalmaznak. Az egyes köztes szakaszok kialakulása a nem kötött hemoglobinból a K i {\displaystyle K_{i}} látszólagos makroszkopikus asszociációs állandóval írható le.

. Az így kapott frakcionált foglaltság a következőképpen fejezhető ki: Y ¯ = 1 4 ⋅ K I + 2 K I I I 2 + 3 K I I I I 3 + 4 K I V 4 1 + K I + K I I I 2 + K I I I I 3 + K I V 4 {\displaystyle {\bar {Y}}={\frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, Bármely n ligandumkötőhellyel rendelkező fehérjére:
Y ¯ = 1 n K I + 2 K I I 2 + … + n K n n 1 + K I + K I I 2 + K I I 2 + … + K n n {\displaystyle {\bar {Y}}={\frac {1}{n}}}{\frac {K_{I}+2K_{II}^{2}+\ldots +nK_{n}^{n}}{1+K_{I}+K_{II}^{2}+\ldots +K_{n}^{n}}}}

ahol n a kötőhelyek számát jelöli és minden K i {\displaystyle K_{i}}

egy kombinált asszociációs állandó, amely i ligandummolekula kötődését írja le. az Adair-féle kezelést a Hill-diagrammal kombinálva jutunk el a kooperativitás modern kísérleti definíciójához (Hill, 1985, Abeliovich, 2005). Az így kapott Hill-koefficiens, vagy helyesebben a Hill-diagram Adair-egyenletből számított meredeksége kimutatható, mint a kötésszám varianciájának és a kötésszám varianciájának hányadosa egy nem kölcsönható kötőhelyekből álló egyenértékű rendszerben. Így a Hill-koefficiens a kooperativitást úgy határozza meg, mint az egyik kötőhely statisztikai függését a többi kötőhely(ek) állapotától.
A Klotz-egyenletSzerkesztés
Irving Klotz kalciumkötő fehérjékkel dolgozva dekonvolutálta az Adair-féle asszociációs állandókat a köztes szakaszok lépcsőzetes kialakulásának figyelembevételével, és a kooperatív kötődést a tömeghatás törvénye által szabályozott elemi folyamatokkal próbálta kifejezni. Az ő keretrendszerében K 1 {\displaystyle K_{1}}

az első ligandummolekula kötődését szabályozó asszociációs állandó, K 2 {\displaystyle K_{2}}

a második ligandummolekula kötődését szabályozó asszociációs állandó (ha az első már kötődött) stb. Az Y ¯ {\displaystyle {\bar {Y}}}

, ez adja: Y ¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … … K n ) n {\displaystyle {\bar {\Y}}={\frac {1}{n}}}{\frac {K_{1}+2K_{1}K_{2}K_{2}^{2}+\ldots +n\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Meg kell jegyezni, hogy a K 1 {\displaystyle K_{1}}}

, K 2 {\displaystyle K_{2}}

stb. nem az egyes kötőhelyekre vonatkoznak. Azt írják le, hogy hány kötőhely van elfoglalva, nem pedig azt, hogy melyek. Ennek a formának megvan az az előnye, hogy a kooperativitás könnyen felismerhető a társulási állandók vizsgálatakor. Ha minden ligandumkötőhely azonos, K {\displaystyle K}

mikroszkopikus asszociációs állandóval, akkor azt várnánk, hogy K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K {\displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}}K,\ldots K_{n}={\frac {1}{n}}}K}

(azaz K i = n – i + 1 i K {\displaystyle K_{i}={\frac {n-i+1}{i}}}K}K}

) kooperativitás hiányában. Pozitív kooperativitással rendelkezünk, ha K i {\displaystyle K_{i}}

e várható értékek fölé esik i > 1 {\displaystyle i>1}

.
A Klotz-egyenletet (amelyet néha Adair-Klotz-egyenletnek is neveznek) még mindig gyakran használják a kísérleti irodalomban a ligandumkötés méréseinek leírására a szekvenciális látszólagos kötési állandókkal.
Pauling-egyenletSzerkesztés
A 20. század közepére megnőtt az érdeklődés olyan modellek iránt, amelyek nemcsak fenomenológiailag írják le a kötési görbéket, hanem a mögöttes biokémiai mechanizmust is kínálják. Linus Pauling újraértelmezte az Adair által megadott egyenletet, feltételezve, hogy állandói a ligandum kötődési állandójának ( K {\displaystyle K}

az alábbi egyenletben) és az együttműködő fehérje alegységei közötti kölcsönhatásból származó energiának ( α {\displaystyle \alpha }

az alábbiakban) a kombinációja. Pauling valójában több egyenletet is levezetett, az alegységek közötti kölcsönhatás mértékétől függően. A hemek lokalizációjára vonatkozó téves feltételezések alapján a hemoglobin oxigénmegkötésének leírására a rosszat választotta, feltételezve, hogy az alegységek négyzetben helyezkednek el. Az alábbi egyenlet a tetraéderes szerkezetre vonatkozó egyenletet adja meg, ami pontosabb lenne a hemoglobin esetében: Y ¯ = K + 3 α K 2 2 + 3 α 3 K 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 + 4 α 3 K 3 3 + α 6 K 4 4 {\displaystyle {\bar {Y}}={\frac {K+3\alpha {}K^{2}^{2}+3\alpha {}^{3}K^{3}^{3}+\alpha {}^{6}K^{4}^{4}}}{1+4K+6\alpha {}K^{2}^{2}+4\alpha {}^{3}K^{3}^{3}^{3}+\alpha {}^{6}K^{4}^{4}^{4}}}}

A KNF modellSzerkesztés
Azokon az eredményeken alapul, amelyek szerint a kooperatív fehérjék szerkezete megváltozik a ligandjukhoz való kötődéskor, Daniel Koshland és munkatársai finomították a Pauling által leírt mechanizmus biokémiai magyarázatát. A Koshland-Némethy-Filmer (KNF) modell feltételezi, hogy minden alegység kétféle konformációban létezhet: aktív vagy inaktív. Az egyik alegységhez kötődő ligandum az adott alegység azonnali konformációváltását idézné elő az inaktívból az aktív konformációba, ezt a mechanizmust “indukált illeszkedésként” írják le. A KNF-modell szerint a kooperativitás az alegységek közötti kölcsönhatásokból ered, amelyek erőssége az érintett alegységek relatív konformációjától függően változik. Tetraéderes szerkezetre (lineáris és négyzetes szerkezeteket is figyelembe vettek) a következő képletet javasolták:
Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B ( K X K t ) 2 + 3 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {\displaystyle {\bar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Hol K X {\displaystyle K_{X}}

az X társulási állandója, K t {\displaystyle K_{t}}

a B és A állapotok aránya ligandum hiányában (“átmenet”), K A B {\displaystyle K_{AB}}

és K B B {\displaystyle K_{BB}}

a szomszédos alegységek párjainak relatív stabilitása egy olyan párhoz képest, ahol mindkét alegység A állapotban van (Megjegyzendő, hogy a KNF papír valójában N s {\displaystyle N_{s}}}

, a foglalt helyek számát, ami itt 4-szerese Y ¯ {\displaystyle {\bar {\bar {Y}}}}

).
Az MWC modellSzerkesztés


A Monod-Wyman-Changeux (MWC) modell az összehangolt alloszterikus átmenetekre egy lépéssel továbbment a termodinamikán és a háromdimenziós konformációkon alapuló kooperativitás vizsgálatával. Eredetileg oligomer fehérjékre fogalmazták meg, szimmetrikusan elrendezett, azonos alegységekkel, amelyek mindegyike egy-egy ligandumkötőhellyel rendelkezik. Eszerint az allosztérikus fehérje két (vagy több) egymással konvertálható konformációs állapota termikus egyensúlyban létezik egymás mellett. Az állapotok – amelyeket gyakran feszesnek (T) és relaxáltnak (R) neveznek – a ligandum molekula iránti affinitásukban különböznek egymástól. A két állapot közötti arányt a magasabb affinitású állapotot stabilizáló ligandum molekulák kötődése szabályozza. Fontos, hogy a molekula minden alegysége egyszerre vált állapotot, ez az úgynevezett “összehangolt átmenet” jelensége.
Az L alloszterikus izomerizációs állandó a két állapot közötti egyensúlyt írja le, amikor nincs ligandum molekula kötve: L = {\displaystyle L={\frac {\left}{\left}}}

. Ha L nagyon nagy, akkor a fehérje nagy része ligandum hiányában T állapotban van. Ha L kicsi (közel egy), akkor az R állapot majdnem ugyanolyan népes, mint a T állapot. A ligandum T és R állapotból való disszociációs állandóinak arányát a c konstans írja le: c = K d R K d T {\displaystyle c={\frac {K_{d}^{R}}{K_{d}^{T}}}}

. Ha c = 1 {\displaystyle c=1}

, akkor mind az R, mind a T állapot azonos affinitással rendelkezik a ligandumhoz, és a ligandum nem befolyásolja az izomerizációt. A c értéke azt is jelzi, hogy a T és R állapotok közötti egyensúly mennyire változik a ligandum megkötésekor: minél kisebb a c, annál inkább eltolódik az egyensúly az R állapot felé egy kötés után. α = K d R {\displaystyle \alpha ={\frac {}{K_{d}^{R}}}}

, a frakcionális foglaltság a következőképpen írható le: Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {Y}}={\frac {\alpha (1+\alpha )^{n-1}+Lc\alpha (1+c\alpha )^{n-1}}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Az alloszterikus fehérjék szigmoid Hill-diagramja ezután úgy elemezhető, mint a T állapotból (alacsony affinitás) az R állapotba (magas affinitás) való fokozatos átmenet a telítettség növekedésével. A Hill-diagram meredeksége szintén függ a telítettségtől, maximális értéke az inflexiós pontban van. A két aszimptoták és az y-tengely közötti metszéspontok lehetővé teszik a két állapotnak a ligandumhoz való affinitásának meghatározását.

A fehérjékben a konformációváltozás gyakran kapcsolódik az aktivitáshoz, illetve a specifikus célpontokkal szembeni aktivitáshoz. Az ilyen aktivitás gyakran az, ami fiziológiailag releváns, vagy amit kísérletileg mérnek. A konformációváltozás mértékét az R ¯ {\displaystyle {\bar {\bar {R}}} állapotfüggvény írja le.

, amely a fehérjének az R {\displaystyle R}

state. Amint az energiadiagram szemlélteti, az R ¯ {\displaystyle {\bar {R}}}

növekszik, ahogy több ligandummolekula kötődik. Az R ¯ {\\displaystyle {\bar {R}}}

a következő: R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {R}}={\frac {(1+\alpha )^{n}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Az MWC modell döntő szempontja, hogy az Y ¯ {\displaystyle {\bar {Y}}}}

és R ¯ {\displaystyle {\bar {R}}}

nem esnek egybe, azaz a frakcionális telítettség nem közvetlen mutatója a konformációs állapotnak (és így az aktivitásnak). Ráadásul a kötődés kooperativitásának és az aktiválás kooperativitásának mértéke nagyon eltérő lehet: szélsőséges esetet a baktériumok flagella-motorja szolgáltat, ahol a Hill-együttható 1,7 a kötődésre és 10,3 az aktiválásra. A válasz szuperlinearitását néha ultraszenzitivitásnak nevezik.
Ha egy allosztérikus fehérje olyan célponthoz kötődik, amely szintén nagyobb affinitással rendelkezik az R állapothoz, akkor a célponthoz való kötődés tovább stabilizálja az R állapotot, ezáltal növeli a ligandum affinitását. Ha viszont egy célpont előnyösen kötődik a T állapothoz, akkor a célpontkötés negatívan hat a ligandum affinitására. Az ilyen célpontokat allosztérikus modulátoroknak nevezzük.
Az MWC keretrendszert a kezdetek óta kibővítették és általánosították. Variációkat javasoltak, például a kettőnél több állapotú fehérjék, a többféle ligandumhoz vagy többféle alloszterikus modulátorhoz kötődő fehérjék és a nem azonos alegységekkel vagy ligandumkötő helyekkel rendelkező fehérjék figyelembevételére.