6.3 Redes de Creencias
La noción de independencia condicional puede utilizarse para dar una representación concisa de muchos dominios. La idea es que, dada una variable aleatoria X, puede existir un pequeño conjunto de variables que afectan directamente al valor de la variable en el sentido de que X es incondicionalmente independiente de otras variables dados los valores de las variables que afectan directamente. El conjunto de variables que afectan localmente se denomina manto de Markov. Esta localidad es la que se aprovecha en una red de creencias. Una red de creencias es un modelo dirigido de dependencia condicional entre un conjunto de variables aleatorias. El enunciado preciso de la independencia condicional en una red de creencia tiene en cuenta la direccionalidad.
Para definir una red de creencia, comience con un conjunto de variables aleatorias que representan todas las características del modelo. Supongamos que estas variables son {X1,…,Xn}.A continuación, seleccione un ordenamiento total de las variables, X1,…,Xn.
La regla de la cadena (Proposición 6.3) muestra cómo descomponer una conjunción en probabilidades condicionales:
P(X1=v1∧X2=v2∧—∧Xn=vn) = ∏i=1n P(Xi=vi|X1=v1∧—∧Xi-1=vi-1).
O, en términos de variables aleatorias y distribuciones de probabilidad,
P(X1, X2,—, Xn) = ∏i=1n P(Xi|X1, —, Xi-1).
Defina los padres de la variable aleatoria Xi, escritosparents(Xi), para ser un conjunto mínimo de predecesores de Xi en el ordenamiento total tal que los otros predecesores de Xi son condicionalmente independientes de Xi dadoparents(Xi). Es decir, padres(Xi) ⊆{X1,…,Xi-1} tal que
P(Xi|Xi-1…X1) = P(Xi|padres(Xi)).
Si existe más de un conjunto mínimo, cualquier conjunto mínimo puede ser elegido para ser los padres. Puede haber más de un conjunto mínimo sólo cuando algunos de los predecesores son funciones deterministas de otros.
Podemos poner la regla de la cadena y la definición de padres juntos, dando
P(X1, X2,—, Xn) = ∏i=1n P(Xi|padres(Xi)).
La probabilidad sobre todas las variables, P(X1, X2,—,Xn), se llama distribución de probabilidad conjunta. Una red de creencia define una factorización de la distribución de probabilidad conjunta, donde las probabilidades condicionales forman factores que se multiplican juntos.
Una red de creencia, también llamada red bayesiana, es un grafo acíclico dirigido (DAG), donde los nodos son variables aleatorias. Hay un arco desde cada elemento de padres(Xi) hacia Xi.Asociado con la red de creencia hay un conjunto de distribuciones de probabilidad condicional – la probabilidad condicional de cada variable dada sus padres (que incluye las probabilidades previas de aquellas variables sin padres).
Así, una red de creencia consiste en
- un DAG, donde cada nodo está etiquetado por una variable aleatoria;
- un dominio para cada variable aleatoria; y
- un conjunto de distribuciones de probabilidad condicional que dan P(X|padres(X)) para cada variable X.
Una red de creencia es acíclica por construcción. La forma en que la cadena gobernadaecompone la conjunción da el ordenamiento. Una variable sólo puede tener predecesores como padres.Diferentes descomposiciones pueden dar lugar a diferentes redes de creencia.
Supongamos que utilizamos las siguientes variables, todas ellas booleanas, en el siguiente orden:
- La manipulación es verdadera cuando se manipula la alarma.
- Incendio es verdadero cuando hay un incendio.
- Alarma es verdadero cuando suena la alarma.
- Humo es verdadero cuando hay humo.
- Saliendo es verdadero si hay muchas personas saliendo del edificio a la vez.
- Informe es verdadero si hay un informe dado por alguien de personas saliendo. Informe es falso si no hay ningún informe de salida.
La variable Informe denota el informe del sensor de que la gente se está yendo. Esta información no es fiable porque la persona que emite dicho informe podría estar gastando una broma, o nadie que pudiera haber dado dicho informe podría haber estado prestando atención. Esta variable se introduce para permitir el condicionamiento de los datos no fiables del sensor. El agente sabe lo que el sensor informa, pero sólo tiene evidencia poco fiable sobre la gente que sale del edificio.Como parte del dominio, asumir las siguientes independencias condicionales:
- El fuego es condicionalmente independiente de Tampering (dada ninguna otra información).
- Alarma depende tanto de Fuego y Tampering. Es decir, no estamos haciendo ninguna suposición de independencia sobre cómo la alarma depende de sus predecesores dado este ordenamiento de variables.
- El humo depende sólo del fuego y es condicionalmente independiente de la manipulación y la alarma dado si hay un incendio.
- Salir sólo depende de la alarma y no directamente del fuego o la manipulación o el humo. Es decir, la salida es condicionalmente independiente de las otras variables dada la alarma.
- El informe sólo depende directamente de la salida.
La red de creencias de la figura 6.1 expresa estas dependencias.
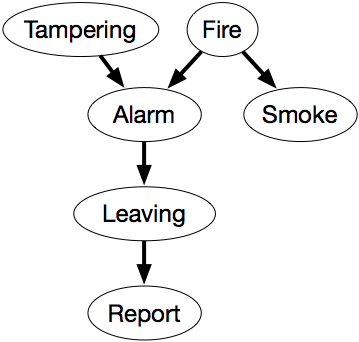
Esta red representa la factorización
P(Manipulación,Incendio,Alarma,Humo,Salida,Informe) = P(Manipulación) ×P(Incendio) ×P(Alarma|Manipulación,Incendio) ×P(Humo|Incendio) ×P(Abandono|Alarma) ×P(Informe|Abandono).
También debemos definir el dominio de cada variable. Supongamos que las variables son booleanas; es decir, tienen dominio {verdadero,falso}. Utilizamos la variante minúscula de la variable para representar el valor verdadero y utilizamos la negación para el valor falso. Así, por ejemplo, Tampering=true se escribe como tampering, y Tampering=false se escribe como ¬tampering.
Los ejemplos que siguen suponen las siguientes probabilidades condicionales:
P(fire) = 0,01
P(alarm | fire ∧tampering) = 0.5
P(alarma | fuego ∧¬tampering) = 0,99
P(alarma |¬fuego ∧tampering) = 0,85
P(alarma |¬fuego ∧¬tampering) = 0,0001
P(humo | fuego ) = 0.9
P(humo | ¬fuego ) = 0,01
P(salida | alarma) = 0,88
P(salida | ¬alarma ) = 0,001
P(informe | salida ) = 0,75
P(informe | ¬salida ) = 0.01
- Para cada cable wi, hay una variable aleatoria, Wi, con dominio {vivo,muerto}, que denota si hay energía en el cable wi. Wi=vivo significa que el cable wi tiene energía. Wi=muerto significa que no hay energía en el cable wi.
- La potencia exterior con dominio {vivo,muerto} denota si hay energía que entra en el edificio.
- Para cada interruptor si, la variable Si_pos denota la posición desi. Tiene el dominio {arriba, abajo}.
- Para cada interruptor si, la variable Si_st denota el estado del interruptor si. Tiene dominio {ok,upside_down,short,intermittent,broken}. Si_st=ok significa que el interruptor si funciona normalmente. Si_st=al revés significa que el interruptor si está instalado al revés. Si_st=corto significa que el interruptor si está cortocircuitado y actúa como un cable. Si_st=roto significa que el interruptor si está roto y no permite que fluya la electricidad.
- Para cada interruptorercbi, la variable Cbi_st tiene dominio {on,off}. Cbi_st=on significa que la energía puede fluir a través de cbi y Cbi_st=off significa que la energía no puede fluir a través de cbi.
- Para cada luz li, la variable Li_st con dominio {ok,intermitente,roto} denota el estado de la luz. Li_st=ok significa que la luz li se encenderá si recibe energía, Li_st=intermitente significa que la luz li se enciende intermitentemente si recibe energía, y Li_st=roto significa que la luz li no funciona.
Seleccionemos un ordenamiento en el que las causas de una variable estén antes de la variable en el ordenamiento. Por ejemplo, la variable de si una luz está encendida viene después de las variables de si la luz está funcionando y si hay energía que llega a la luz.
Si la luz l1 está encendida depende sólo de si hay energía en el cable w0 y si la luz l1 está funcionando correctamente. Otras variables, como la posición del interruptor s1, si la luz l2 está encendida, o quién es la Reina de Canadá, son irrelevantes. Así, los padres de L1_lit son W0 y L1_st.
Consideremos la variable W0, que representa si hay energía en el cable w0. Si supiéramos si hay energía en los cables w1 yw2, y conociéramos la posición del interruptor s2 y si el interruptor funciona correctamente, el valor de las otras variables (aparte de L1_lit) no afectaría a nuestra creencia de que hay energía en el cable w0. Por lo tanto, los padres de W0 deberían ser S2_Pos, S2_st, W1 y W2.
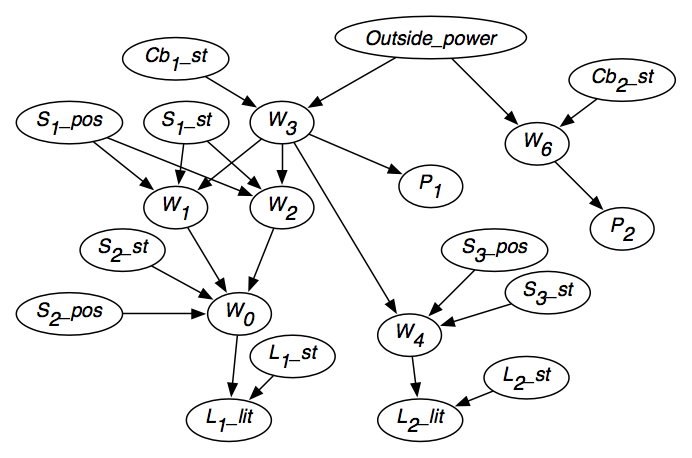
La figura 6.2 muestra la red de creencia resultante después de que se haya considerado la independencia de cada variable.La red de creencia también contiene los dominios de las variables, como se indica en la figura, y las probabilidades condicionales de cada variable dadas sus padres.
Para la variable W1, se deben especificar las siguientes probabilidades condicionales:
P(W1=vivo|S1_pos=arriba ∧S1_st=ok ∧W3=vivo)
P(W1=vivo|S1_pos=arriba ∧S1_st=ok ∧W3=dead)
P(W1=live|S1_pos=up ∧S1_st=upside_down ∧W3=live)
… P(W1=vivo|S1_pos=abajo ∧S1_st=roto ∧W3=muerto).
Hay dos valores para S1_pos, cinco valores para S1_ok, ydos valores para W3, por lo que hay 2×5 ×2 = 20 casos diferentes en los que se debe especificar un valor para W1=vivo. En lo que respecta a la teoría de la probabilidad, la probabilidad de W1=vivo en estos 20 casos podría asignarse de forma arbitraria. Por supuesto, el conocimiento del dominio limita los valores que tienen sentido. Los valores de W1=muerto pueden calcularse a partir de los valores de W1=vivo para cada uno de estos casos.
Debido a que la variable S1_st no tiene padres, requiere una distribución previa, que puede especificarse como las probabilidades de todos los valores menos uno; el valor restante puede derivarse de la restricción de que todas las probabilidades sumen 1. Así, para especificar la distribución de S1_st, deben especificarse cuatro de las cinco probabilidades siguientes:
P(S1_st=ok)
P(S1_st=upside_down)
P(S1_st=short)
P(S1_st=intermittent)
P(S1_st=broken)
The other variables are represented analogously.
Un grafo de creencias es una representación gráfica de la independencia condicional.La independencia nos permite representar los efectos directos dentro del grafo y prescribe qué probabilidades deben especificarse. Las probabilidades posteriores arbitrarias pueden derivarse del grafo.
El supuesto de independencia incluido en un grafo de creencia es el siguiente: cada variable aleatoria es condicionalmente independiente de sus no descendientes dados sus progenitores. Es decir, si X es una variable aleatoria con padres Y1,…, Yn, todas las variables aleatorias que no son descendientes deX son condicionalmente independientes de X dado Y1 ,…, Yn:
P(X|Y1,…, Yn,R)=P(X|Y1,…, Yn),
si R no implica un descendiente de X. Para esta definición, incluimos a X como descendiente de sí mismo. El lado derecho de esta ecuación es la forma de las probabilidades que se especifican como parte de la red de creencia.R puede implicar a los ancestros de X y otros nodos siempre que no sean descendientes de X. La suposición de independencia establece que toda la influencia de las variables no descendientes se captura conociendo el valor de los padres de X.
A menudo, nos referimos sólo al DAG etiquetado como una red de creencia. Cuando se hace esto, es importante recordar que un dominio para cada variable y un conjunto de distribuciones de probabilidad condicional son también parte de la red.
El número de probabilidades que deben especificarse para cada variable es exponencial en el número de padres de la variable.El supuesto de independencia es útil en la medida en que el número de variables que afectan directamente a otra variable es pequeño. Debe ordenar las variables de forma que los nodos tengan el menor número posible de padres.
Redes de creencias y causalidad
Las redes de creencias se han denominado a menudo redes causales y se ha afirmado que son una buena representación de la causalidad.Recuerde que un modelo causal predice el resultado de las intervenciones.Suponga que tiene en mente un modelo causal de un dominio, donde el dominio se especifica en términos de un conjunto de variables aleatorias. Para cada par de variables aleatorias X1y X2, si existe una conexión causal directa de X1 a X2 (es decir, intervenir para cambiar X1 en algún contexto de otras variables afecta a X2 y esto no puede modelarse teniendo alguna variable interviniente), añada un arco deX1 a X2. Es de esperar que el modelo causal obedezca al supuesto de independencia de la red de creencias. Por lo tanto, todas las conclusiones de la red de creencias serían válidas.
También se esperaría que dicho gráfico fuera acíclico; no se desea que algo se cause a sí mismo. Esta suposición es razonable si se considera que las variables aleatorias representan eventos particulares en lugar de tipos de eventos. Por ejemplo, considere una cadena causal en la que “estar estresado” le hace “trabajar de forma ineficiente”, lo que, a su vez, le hace “estar estresado”. Para romper el ciclo aparente, podemos representar “estar estresado” en diferentes etapas como diferentes variables aleatorias que se refieren a diferentes tiempos. Estar estresado en el pasado hace que no trabajes bien en ese momento, lo que hace que estés estresado en el futuro. Las variables deben cumplir el principio de claridad y tener un significado bien definido. Las variables no deben ser vistas como tipos de eventos.
La red de creencias en sí misma no tiene nada que decir sobre la causalidad, y puede representar la independencia no causal, pero parece particularmente apropiada cuando hay causalidad en un dominio. Añadir arcos que representen la causalidad local tiende a producir una red de creencia pequeña. La red de creencia de la figura 6.2 muestra cómo se puede hacer esto para un dominio simple.
La red causal modela las intervenciones. Si alguien forzara artificialmente a una variable a tener un valor determinado, los descendientes de la variable -pero ningún otro nodo- se verían afectados. Por último, puede ver cómo la causalidad en las redes de creencias se relaciona con el razonamiento causal y probatorio que se discute en la sección 5.7. Una red de creencia causal puede verse como algo alejado de la axiomatización en una dirección causal. El razonamiento en las redes de creencia corresponde a la abducción a las causas y a la predicción a partir de ellas. Existe un mapeo directo entre el punto de vista abductivo basado en la lógica que se discute en la sección 5.7 y las redes de creencias: Las redes de creencias pueden modelarse como programas lógicos con probabilidades sobre posibles hipótesis. Esto se describe en la sección 14.3.
Nótese la restricción “cada variable aleatoria es condicionalmente independiente de sus no descendientes dados sus padres” en la definición de la independencia codificada en una red de creencias. SiR contiene un descendiente de la variable X, el supuesto de independencia no es directamente aplicable.
La variable S1_pos no tiene padres. Así, la independencia incrustada en la red de creencias especifica que P(S1_pos=up|A) =P(S1_pos=up) para cualquier A que no incluya un descendiente deS1_pos. Si A incluye un descendiente de S1_pos=up -por ejemplo, si A es S2_pos=up∧L1_lit=true- la suposición de independencia no puede aplicarse directamente.
Esta red puede utilizarse de varias maneras:
- Al condicionar el conocimiento de que los interruptores y los disyuntores están bien, y los valores de la potencia exterior y la posición de los interruptores, esta red puede simular cómo debería funcionar la iluminación.
- Dados los valores de la potencia exterior y la posición de los interruptores, la red puede inferir la probabilidad de cualquier resultado – por ejemplo, la probabilidad de que l1 se encienda.
- Dados los valores de los interruptores y si las luces están encendidas, se puede inferir la probabilidad posterior de que cada interruptor o disyuntor esté en cualquier estado particular.
- Dadas algunas observaciones, la red se puede utilizar para razonar hacia atrás para determinar la posición más probable de los interruptores.
- Dadas algunas posiciones de los interruptores, algunas salidas y algunos valores intermedios, la red se puede utilizar para determinar la probabilidad de cualquier otra variable en la red.
Una red de creencia especifica una distribución de probabilidad conjunta de la que se pueden derivar probabilidades condicionales arbitrarias. Una red puede ser consultada pidiendo la probabilidad condicional de cualquier variable condicionada a los valores de cualquier otra variable. Esto suele hacerse proporcionando observaciones sobre algunas variables y preguntando por otra variable.
P(incendio) = 0,01
P(informe ) = 0,028
P(humo) = 0.0189
Al observar el informe se obtiene lo siguiente:
P(fuego|informe)= 0,2305
P(humo|informe) = 0,215
Como era de esperar, la probabilidad tanto de manipulación como de incendio aumenta con el informe. Dado que el fuego aumenta, también lo hace la probabilidad de humo.
Supongamos, en cambio, que se observa humo:
P(incendio|humo) = 0,476
P(informe |humo) = 0,320
Nótese que la probabilidad de manipulación no se ve afectada por la observación de humo; sin embargo, las probabilidades de informe e incendio aumentan.
Supongamos que se observan tanto la denuncia como el humo:
P(incendio |denuncia ∧humo) = 0,964
Observar ambos hace que el incendio sea aún más probable. Sin embargo, en el contexto del informe, la presencia de humo hace que la manipulación sea menos probable. Esto se debe a que el informe se explica por el fuego, que ahora es más probable.
Supongamos que se observa el informe, pero no el humo:
P(fuego|informe ∧¬humo) = 0,0294
En el contexto del informe, el fuego se vuelve mucho menos probable y la probabilidad de manipulación aumenta para explicar el informe.
Este ejemplo ilustra cómo la suposición de independencia de la red de creencia da conclusiones de sentido común y también demuestra cómo la explicación es una consecuencia de la suposición de independencia de una red de creencia.
- 6.3.1 Construcción de redes de creencia