Christian Bohr e il concetto di legame cooperativoModifica
Nel 1904, Christian Bohr studiò il legame dell’emoglobina all’ossigeno in diverse condizioni. Tracciando la saturazione dell’emoglobina con l’ossigeno in funzione della pressione parziale dell’ossigeno, ottenne una curva sigmoidale (o “a forma di S”). Questo indica che più l’ossigeno è legato all’emoglobina, più è facile che altro ossigeno si leghi – fino a quando tutti i siti di legame sono saturi. Inoltre, Bohr notò che l’aumento della pressione di CO2 spostava questa curva verso destra – cioè concentrazioni più alte di CO2 rendono più difficile per l’emoglobina legare l’ossigeno. Quest’ultimo fenomeno, insieme all’osservazione che l’affinità dell’emoglobina per l’ossigeno aumenta all’aumentare del pH, è noto come effetto Bohr.

Si dice che una molecola di recettore presenta un legame cooperativo se il suo legame al ligando scala in modo non lineare con la concentrazione del ligando. La cooperatività può essere positiva (se il legame di una molecola di ligando aumenta l’affinità apparente del recettore, e quindi aumenta la possibilità di legame di un’altra molecola di ligando) o negativa (se il legame di una molecola di ligando diminuisce l’affinità e quindi rende meno probabile il legame di altre molecole di ligando). L'”occupazione frazionaria” Y ¯ {displaystyle {\bar {Y}}}

di un recettore con un dato ligando è definita come la quantità di siti di legame legati al ligando divisa per la quantità totale di siti di legame del ligando: Y ¯ = + = {\displaystyle {\bar {Y}}={frac {}+}={\frac {}}}

Se Y ¯ = 0 {\displaystyle {\bar {Y}=0}

, allora la proteina è completamente non legata, e se Y ¯ = 1 {\displaystyle {{barra {Y}=1}

, è completamente satura. Se il tracciato di Y ¯ {\displaystyle {\bar {Y}}}

all’equilibrio in funzione della concentrazione del ligando è di forma sigmoidale, come osservato da Bohr per l’emoglobina, questo indica una cooperatività positiva. Se non lo è, nessuna affermazione può essere fatta sulla cooperatività guardando solo questo grafico.
Il concetto di legame cooperativo si applica solo a molecole o complessi con più di un sito di legame del ligando. Se esistono diversi siti di legame del ligando, ma il legame del ligando a qualsiasi sito non influenza gli altri, si dice che il recettore non è cooperativo. La cooperatività può essere omotropa, se un ligando influenza il legame di ligandi dello stesso tipo, o eterotropa, se influenza il legame di altri tipi di ligandi. Nel caso dell’emoglobina, Bohr ha osservato una cooperatività positiva omotropa (il legame dell’ossigeno facilita il legame di più ossigeno) e una cooperatività negativa eterotropa (il legame della CO2 riduce la capacità dell’emoglobina di legare l’ossigeno.)
Nel corso del XX secolo, sono state sviluppate varie strutture per descrivere il legame di un ligando a una proteina con più di un sito di legame e gli effetti cooperativi osservati in questo contesto.
L’equazione di HillEdit
La prima descrizione del legame cooperativo a una proteina multi-sito fu sviluppata da A.V. Hill. Basandosi sulle osservazioni del legame dell’ossigeno all’emoglobina e sull’idea che la cooperatività derivasse dall’aggregazione delle molecole di emoglobina, ciascuna delle quali legava una molecola di ossigeno, Hill suggerì un’equazione fenomenologica che da allora ha preso il suo nome:
Y ¯ = K ⋅ n 1 + K ⋅ n = n K ∗ + n = n K d n + n {\displaystyle {\bar {Y}={\frac {K\cdot {}^{n}}{1+K\cdot {^{n}}={\frac {^{n}}{K^{*}+^{n}}={\frac {^{n}{K_{d}^{n}+^{n}}}}

dove n {displaystyle n}

è il “Coefficiente di Hill”, {\displaystyle }

denota la concentrazione del ligando, K {displaystyle K}

denota una costante di associazione apparente (usata nella forma originale dell’equazione), K ∗ {displaystyle K^{*}}

è una costante di dissociazione empirica, e K d {displaystyle K_{d}

una costante di dissociazione microscopica (usata nelle forme moderne dell’equazione, ed equivalente ad un E C 50 {displaystyle \mathrm {EC} _{50}}

). Se n < 1 {\displaystyle n<1}

, il sistema mostra una cooperatività negativa, mentre la cooperatività è positiva se n > 1 {\displaystyle n>1}

. Il numero totale di siti di legame del ligando è un limite superiore per n {\displaystyle n}

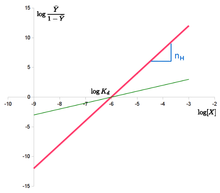
. L’equazione di Hill può essere linearizzata come: log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}=n\cdot {}log-n\cdot {}\log K_{d}}
Il “grafico di Hill” si ottiene tracciando il log Y ¯ 1 – Y ¯
Si ottiene tracciando il log Y ¯ 1 – Y ¯
Si ottiene tracciando il log Y ¯ 1 – Y ¯
contro log {displaystyle \log}

. Nel caso dell’equazione di Hill, è una linea con pendenza n H {\displaystyle n_{H}

e intercetta log ( K d ) {\displaystyle \log(K_{d})}

. Questo significa che la cooperatività è assunta come fissa, cioè non cambia con la saturazione. Significa anche che i siti di legame mostrano sempre la stessa affinità, e la cooperatività non deriva da un’affinità che aumenta con la concentrazione del ligando.
L’equazione di AdairEdit
G.S. Adair trovò che il grafico di Hill per l’emoglobina non era una linea retta, e ipotizzò che l’affinità di legame non fosse un termine fisso, ma dipendente dalla saturazione del ligando. Avendo dimostrato che l’emoglobina conteneva quattro emi (e quindi siti di legame per l’ossigeno), ha lavorato dal presupposto che l’emoglobina completamente satura si forma in fasi, con forme intermedie con una, due o tre molecole di ossigeno legate. La formazione di ogni stadio intermedio dall’emoglobina non legata può essere descritta utilizzando una costante di associazione macroscopica apparente K i {displaystyle K_{i}}

. L’occupazione frazionaria risultante può essere espressa come: Y ¯ = 1 4 ⋅ K I + 2 K I I 2 + 3 K I I I 3 + 4 K I V 4 1 + K I + K I I 2 + K I I I 3 + K I V 4 {\displaystyle {\bar {Y}}={\frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, per qualsiasi proteina con n siti di legame del ligando:
Y ¯ = 1 n K I + 2 K I I 2 + … + n K n n 1 + K I + K I I 2 + … + K n n {\displaystyle {\bar {Y}={\frac {1}{n}}{frac {K_{I}+2K_{II}^{2}+nK_{n}^{n}}{1+K_{I}+K_{II}^{2}+K_{n}^{n}}}}

dove n indica il numero di siti di legame e ogni K i {displaystyle K_{i}}

è una costante di associazione combinata, che descrive il legame di i molecole di legante.Combinando il trattamento Adair con il diagramma di Hill, si arriva alla moderna definizione sperimentale di cooperatività (Hill, 1985, Abeliovich, 2005). Il coefficiente di Hill risultante, o più correttamente la pendenza del diagramma di Hill come calcolato dall’equazione di Adair, può essere dimostrato essere il rapporto tra la varianza del numero di legame e la varianza del numero di legame in un sistema equivalente di siti di legame non interagenti. Così, il coefficiente di Hill definisce la cooperatività come una dipendenza statistica di un sito di legame dallo stato degli altri siti.
L’equazione di KlotzModifica
Lavorando sulle proteine leganti il calcio, Irving Klotz deconvolse le costanti di associazione di Adair considerando la formazione graduale degli stadi intermedi, e cercò di esprimere il legame cooperativo in termini di processi elementari governati dalla legge di azione di massa. Nel suo quadro, K 1 {displaystyle K_{1}}

è la costante di associazione che governa il legame della prima molecola di ligando, K 2 {displaystyle K_{2}}

è la costante di associazione che governa il legame della seconda molecola di ligando (una volta che la prima è già legata) ecc. Per Y ¯ {displaystyle {\bar {Y}}}

, questo dà: Y ¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … K n ) n {\displaystyle {\frac {\frac {1}{n}}{\frac {K_{1}+2K_{1}K_{2}^{2}++n\frac {K_{1}K_{2}^{2} K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

Si noti che le costanti K 1 {displaystyle K_{1}

, K 2 {displaystyle K_{2}

e così via non si riferiscono a singoli siti di legame. Descrivono quanti siti di legame sono occupati, piuttosto che quali. Questa forma ha il vantaggio che la cooperatività è facilmente riconosciuta quando si considerano le costanti di associazione. Se tutti i siti di legame del ligando sono identici con una costante di associazione microscopica K {\displaystyle K}

, ci si aspetta K 1 = n K , K 2 = n – 1 2 K , … K n = 1 n K {\displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}K,\ldots K_{n}={\frac {1}{n}}K}

(cioè K i = n – i + 1 i K {\displaystyle K_{i}={frac {n-i+1}{i}K}

) in assenza di cooperatività. Abbiamo una cooperatività positiva se K i {displaystyle K_{i}}

si trova sopra questi valori attesi per i > 1 {\displaystyle i>1}

.
L’equazione di Klotz (che a volte è anche chiamata equazione di Adair-Klotz) è ancora spesso usata nella letteratura sperimentale per descrivere le misure di legame dei ligandi in termini di costanti di legame apparenti sequenziali.
Equazione di PaulingModifica
A metà del XX secolo, ci fu un crescente interesse per modelli che non solo descrivessero fenomenologicamente le curve di legame, ma offrissero un meccanismo biochimico sottostante. Linus Pauling reinterpretò l’equazione fornita da Adair, assumendo che le sue costanti fossero la combinazione della costante di legame per il ligando ( K {displaystyle K}

nell’equazione sottostante) e l’energia proveniente dall’interazione tra le subunità della proteina cooperativa ( α {displaystyle \alpha }

sotto). Pauling ha effettivamente derivato diverse equazioni, a seconda del grado di interazione tra le subunità. Sulla base di ipotesi errate sulla localizzazione degli emi, ha optato per quella sbagliata per descrivere il legame dell’ossigeno da parte dell’emoglobina, assumendo che le subunità fossero disposte in un quadrato. L’equazione qui sotto fornisce l’equazione per una struttura tetraedrica, che sarebbe più accurata nel caso dell’emoglobina: Y ¯ = K + 3 α K 2 2 + 3 α 3 K 3 3 + α 6 K 4 4 1 + 4 K + 6 α K 2 2 + 4 α 3 K 3 + α 6 K 4 4 {\displaystyle {\bar {Y}={\frac {K+3\alpha {K^{2}^{2}+3\alfa {}^{3}K^{3}^{3}+{alpha {}^{6}K^{4}^{4}{1+4K+6\alfa {}K^{2}^{2}+4\alfa {}^{3}K^{3}^{3}^{3}++{4}}}}}

Il modello KNFEdit
Basato sui risultati che mostrano che la struttura delle proteine cooperative cambiava quando si legavano al loro ligando, Daniel Koshland e colleghi hanno raffinato la spiegazione biochimica del meccanismo descritto da Pauling. Il modello Koshland-Némethy-Filmer (KNF) presuppone che ogni subunità possa esistere in una delle due conformazioni: attiva o inattiva. Il legame del ligando a una subunità indurrebbe un cambiamento conformazionale immediato di quella subunità dalla conformazione inattiva a quella attiva, un meccanismo descritto come “adattamento indotto”. La cooperatività, secondo il modello KNF, deriverebbe dalle interazioni tra le subunità, la cui forza varia a seconda delle conformazioni relative delle subunità coinvolte. Per una struttura tetraedrica (hanno considerato anche strutture lineari e quadrate), hanno proposto la seguente formula:
Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B ( K X K t ) 2 + 3 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {\displaystyle {\bar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

dove K X {displaystyle K_{X}}

è la costante di associazione per X, K t {displaystyle K_{t}

è il rapporto tra gli stati B e A in assenza di ligando (“transizione”), K A B {\displaystyle K_{AB}

e K B B {\displaystyle K_{BB}

sono le stabilità relative di coppie di subunità vicine rispetto a una coppia in cui entrambe le subunità sono nello stato A (si noti che il documento KNF in realtà presenta N s {displaystyle N_{s}

, il numero di siti occupati, che è qui 4 volte Y ¯ {\displaystyle {\bar {Y}}

).
Il modello MWCModifica


Il modello Monod-Wyman-Changeux (MWC) per le transizioni allosteriche concertate ha fatto un passo avanti esplorando la cooperatività basata sulla termodinamica e sulle conformazioni tridimensionali. È stato originariamente formulato per proteine oligomeriche con subunità identiche disposte simmetricamente, ognuna delle quali ha un sito di legame del ligando. Secondo questa struttura, due (o più) stati conformazionali interconvertibili di una proteina allosterica coesistono in un equilibrio termico. Gli stati – spesso chiamati tesi (T) e rilassati (R) – differiscono in affinità per la molecola del ligando. Il rapporto tra i due stati è regolato dal legame di molecole di legante che stabilizza lo stato a maggiore affinità. È importante notare che tutte le subunità di una molecola cambiano stato allo stesso tempo, un fenomeno noto come “transizione concertata”.
La costante di isomerizzazione allosterica L descrive l’equilibrio tra i due stati quando nessuna molecola legante è legata: L = {displaystyle L={{frac {{sinistra}{sinistra}}

. Se L è molto grande, la maggior parte della proteina esiste nello stato T in assenza di ligando. Se L è piccolo (vicino a uno), lo stato R è quasi altrettanto popolato dello stato T. Il rapporto tra le costanti di dissociazione del ligando dagli stati T e R è descritto dalla costante c: c = K d R K d T {displaystyle c={\frac {K_{d}^{R}}{K_{d}^{T}}}}

. Se c = 1 {\displaystyle c=1}

, entrambi gli stati R e T hanno la stessa affinità per il ligando e il ligando non influenza l’isomerizzazione. Il valore di c indica anche quanto cambia l’equilibrio tra gli stati T e R al momento del legame del ligando: più piccolo è c, più l’equilibrio si sposta verso lo stato R dopo un legame. Con α = K d R {displaystyle \alpha ={frac {}{K_{d}^{R}}}}

, l’occupazione frazionaria è descritta come: Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n – 1 ( 1 + α ) n + L ( 1 + c α ) n {\displaystyle {\bar {Y}}={\frac {\alpha (1+\alpha )^{n-1}+Lc\alpha (1+c\alpha )^{n-1}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}

Il sigmoide Hill plot delle proteine allosteriche può quindi essere analizzato come una progressiva transizione dallo stato T (bassa affinità) allo stato R (alta affinità) all’aumentare della saturazione. Anche la pendenza dell’Hill plot dipende dalla saturazione, con un valore massimo nel punto di inflessione. Le intercette tra i due asintoti e l’asse y permettono di determinare le affinità di entrambi gli stati per il ligando.

Nelle proteine, il cambiamento conformazionale è spesso associato all’attività, o all’attività verso obiettivi specifici. Tale attività è spesso ciò che è fisiologicamente rilevante o ciò che viene misurato sperimentalmente. Il grado di cambiamento conformazionale è descritto dalla funzione di stato R ¯ {displaystyle {\bar {R}}}

, che denota la frazione di proteina presente nella R {\displaystyle R}

state. Come illustra il diagramma energetico, R ¯ {displaystyle {\bar {R}}}

aumenta quando si legano più molecole di legante. L’espressione per R ¯ {displaystyle {\bar {R}}}

è: R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {displaystyle {\bar {R}}={\frac {(1+alpha )^{n}}{(1+alpha )^{n}+L(1+c\alpha )^{n}}}}

Un aspetto cruciale del modello MWC è che le curve per Y ¯ {\displaystyle {\bar {Y}}

e R ¯ {displaystyle {{barra {R}}

non coincidono, cioè la saturazione frazionaria non è un indicatore diretto dello stato conformazionale (e quindi, dell’attività). Inoltre, le estensioni della cooperatività del legame e della cooperatività dell’attivazione possono essere molto diverse: un caso estremo è fornito dal motore della flagella batterica con un coefficiente di Hill di 1,7 per il legame e 10,3 per l’attivazione. La sovra-linearità della risposta è talvolta chiamata ultrasensibilità.
Se una proteina allosterica si lega a un bersaglio che ha anche una maggiore affinità per lo stato R, allora il legame del bersaglio stabilizza ulteriormente lo stato R, aumentando così l’affinità del ligando. Se, d’altra parte, un bersaglio si lega preferenzialmente allo stato T, allora il legame del bersaglio avrà un effetto negativo sull’affinità del ligando. Tali bersagli sono chiamati modulatori allosterici.
Dal suo inizio, il quadro MWC è stato esteso e generalizzato. Sono state proposte delle variazioni, per esempio per soddisfare le proteine con più di due stati, proteine che si legano a diversi tipi di ligandi o a diversi tipi di modulatori allosterici e proteine con subunità o siti di legame del ligando non identici.