ヒル式のヒルプロット（赤）は、曲線の傾きがヒル係数で、X軸との切片が見かけの解離定数であることを表している。 緑線は非協同曲線を示す。

Y ¯ = K ⋅ n 1 + K ⋅ n = K ∗ + n = n K d n + n {displaystyle {bar {Y}}={frac {Kcdot {}^{n}}{1+K^{n}}}={frac {^{*}+^{n}}}={K_d}^{n}{N}{K} +{N}}}}{frac{n}} {} + {}n}}} {k{d{*}+^{n}}}} {}n

ここでn {θdplaystyle n}とする。

は「ヒル係数」、{displaystyle } は「ヒル係数」。

はリガンド濃度、K {displaystyle K}

は見かけの会合定数（式の原形で使用）、K ∗ {displaystyle K^{*}} はリガンド濃度、K ｛Displaystyle K^{*} ｛DISPLAYS} ｝はリガンド濃度、K ｛Displaystyle K^{*} ｝はリガンド濃度を表す。

は経験的解離定数、K d {displaystyle K_{d}} は

は微視的解離定数（現代の方程式で用いられ、E C 50 {displaystyle \mathrm {EC}に相当する）である。 _{50}}

) 。 If n < 1 {displaystyle n<1}.

では負の協力性を示し、n > 1 {displaystyle n>1} では協力性が正となる。

. リガンド結合部位の総数は、nの上界{displaystyle n}である。

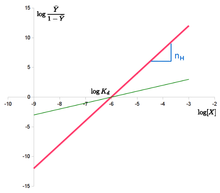
. Hill方程式は次のように線形化できます： log Y ¯ 1 – Y ¯ = n ⋅ log – n ⋅ log K d {displaystyle \log {frac {}bar {Y}{1-{bar {Y}}}=n}cdot{}・ncdot {}log K_{d}} {d}}。

The “Hill plot” is obtained by plotting log Y¯ 1 – Y¯ {}displaystyle \log {}frac {}bar {Y}}{1-{bar {Y}}}を描画することにより、”Hill plot “が得られる。

versus log {displaystyle \log}.

. Hill方程式の場合、傾きn H {displaystyle n_{H}}の直線となる。

and intercept log ( K d ) {displaystyle \log(K_{d}) } }.

. これは、協同性が固定されている、つまり飽和によって変化しないと仮定していることを意味する。 また、結合部位は常に同じ親和性を示し、リガンド濃度に応じて親和性が増加するようなことはないことを意味する。

Adair equationEdit

G.S. Adairはヘモグロビンのヒルプロットが直線でないことを発見し、結合親和力が固定項ではなくリガンド飽和に依存しているという仮説を立てました。 ヘモグロビンには4つのヘムがあり、酸素との結合部位があることを明らかにした彼は、完全飽和ヘモグロビンは、1、2、3個の酸素分子が結合した中間型と段階的に形成されると仮定し、研究を進めた。 結合していないヘモグロビンから各中間体が形成される様子は、巨視的な結合定数K i {displaystyle K_{i}} で記述することができる。

………………………..。 その結果、分数占有率は次のように表すことができる。 Y ¯ = 1 4 ⋅ K I + 2 K I 2 + 3 K I I 3 + 4 K I V 4 1 + K I + K I 2 + K I I 3 + K I V 4 {displaystyle {bar Y}}={{frac {1}{4}}\cdot {}{\frac {K_{I}+2K_{II}^{2}+3K_{III}^{3}+4K_{IV}^{4}}{1+K_{I}+K_{II}^{2}+K_{III}^{3}+K_{IV}^{4}}}}

Or, n個のリガンド結合部位を持つ任意のタンパク質の場合。

Y ¯ = 1 n K I + 2 K I I 2 + … + n K n n 1 + K I + K I I 2 + … + K n n {displaystyle {}}={frac {1}{n}}{frac {K_{I}+2K_{II}^{2}+ldots +nK_{n}^{n}}{1+K_{I}+K_{II}^{2}+ldots +K_{n}^{n}}}}

ここで、nは結合サイトの数を表し、各K i {displaystyle K_{i}} は、以下の通りである。｝

は結合定数で、i個のリガンド分子の結合を記述する。Adair処理とHillプロットを組み合わせることで、現代の実験による協同性の定義にたどり着く（Hill、1985、Abelovich、2005年）。 結果として得られるヒル係数、より正確にはアデア式から計算されるヒルプロットの傾きは、結合数の分散と非相互作用結合部位の等価系における結合数の分散の間の比であることを示すことができる。 このように、ヒル係数は、ある結合部位が他の結合部位の状態に統計的に依存することで、協力性を定義している。

Klotzの式編集

カルシウム結合タンパク質を研究していたKlotzは、中間段階の段階的な形成を考慮してAdairの結合定数を分解し、質量作用法に支配される素過程の観点から協力的結合を表現しようとした。 彼の枠組みでは、K 1 {displaystyle K_{1}} は

は最初のリガンド分子の結合を支配する会合定数、K 2 {displaystyle K_{2}} は

2番目のリガンド分子の結合を支配する会合定数（1番目の分子が既に結合している場合）等である。 Yの場合、{displaystyle {bar {Y}}は、以下の通りである。｝

, これは以下を与える。 Y ¯ = 1 n K 1 + 2 K 1 K 2 2 + … + n ( K 1 K 2 … K n ) n 1 + K 1 + K 1 K 2 2 + … + ( K 1 K 2 … K n ) n { {displaystyle {bar {Y}}={{frac {1}{n}}}{{frac {K_{1}+2K_{1}K_{2}^{2}+⑭left(K_{1}K_{2}⓪dots) K_{n}\right)^{n}}{1+K_{1}+K_{1}K_{2}^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)^{n}}}}

注目すべきは、定数K 1 {displaystyle K_{1}} であることである。｝

, K 2 {}displaystyle K_{2}}.

などは、個々の結合部位に関係しない。 それらは、どの結合部位というよりも、どのように多くの結合部位が占有されているかを記述している。 この形式には、会合定数を考える際に、協力性が容易に認識できるという利点がある。 もし全てのリガンド結合部位が微視的な会合定数K {displaystyle K}

で同一であれば、K 1 = n K , K 2 = n – 1 2 K , …と予想されるであろう。 K n = 1 n K {displaystyle K_{1}=nK,K_{2}={frac {n-1}{2}}K,\ldots K_{n}={frac {1}{n}}K}

K_{1}=nK,K_{2}={frac {n-1}{2}}K,\協調性がない場合、K i = n – i + 1 i K {displaystyle K_{i}={Chenfrac {n-i+1}{i}}K}

) であることがわかる。 K i { {displaystyle K_{i}} の場合、正の協同性がある。

はi > 1 {displaystyle i>1} においてこれらの期待値より上に位置する。

.

Klotz equation (Adair-Klotz equation とも呼ばれる) は、リガンド結合の測定値を連続した見かけの結合定数で表すために、今でも実験文献でよく使われている。

Pauling equationEdit

20世紀の半ばまでに、結合曲線を現象的に表すだけでなく、根底にある生物化学的メカニズムを提供するモデルへの関心が高まってきた。 Linus Paulingは、Adairの提供した式を再解釈し、彼の定数はリガンドの結合定数( K {displaystyle K}

in the equation below )と協同作用タンパク質のサブユニット間の相互作用からくるエネルギー ( α {displaystyle \ }

below )を合わせたものと想定している。 ポーリングは実際には、サブユニット間の相互作用の度合いに応じて、いくつかの方程式を導き出した。 ヘムの局在についての誤った仮定に基づき、彼はサブユニットが正方形に配置されていると仮定して、ヘモグロビンによる酸素結合を記述する誤った方程式を選択したのである。 以下の式は、ヘモグロビンの場合、より正確な四面体構造の方程式を提供する。 Y ¯ = K + 3 α K 2 + 3 α 3 K 3 + α 6 K 4 1 + 4 K + 6 α 6 K 2 + 4 α 3 K 3 + 4 {displaystyle {bar {Y}}={}frac {K+3}alpha {K^{2}^{2}+3alpha {}^{3}K^{3}^{3}+alpha {}^{6}K^{4}^{4}}{1+4K+6alpha {}K^{2}^{2}+4alpha {}^{3}K^{3}^{3}+alpha {}^{6}K^{4}^{4}}}}}

The KNF modelEdit

Cooperative proteinがリガンドに結合すると構造が変化することを示す結果を基にしたもの。 ダニエル・コシュランドらは、ポーリングが説明したメカニズムの生化学的な説明を改良した。 Koshland-Némethy-Filmer（KNF）モデルは、各サブユニットが活性型と非活性型の2つのコンフォメーションで存在できると仮定している。 リガンドが一方のサブユニットに結合すると、そのサブユニットは直ちに不活性型から活性型にコンフォメーション変化する。このメカニズムは、「誘導結合」と呼ばれている。 KNFモデルによれば、協力性はサブユニット間の相互作用から生じ、その強さは関係するサブユニットの相対的なコンフォメーションによって変化する。 四面体構造（彼らは直線構造や正方形構造も考慮した）に対して、彼らは以下の式を提案した。

Y ¯ = K A B 3 ( K X K t ) + 3 K A B 4 K B B ( K X K t ) 2 + 3 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 1 + 4 K A B 3 ( K X K t ) + 6 K A B 4 K B ( K X K t ) 2 + 4 K A B 3 K B B 3 ( K X K t ) 3 + K B B 6 ( K X K t ) 4 {}displaystyle {Thartsbar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t})+3K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}{1+4K_{AB}^{3}(K_{X}K_{t})+6K_{AB}^{4}K_{BB}(K_{X}K_{t})^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t})^{3}+K_{BB}^{6}(K_{X}K_{t})^{4}}}}

Where K X {displaystyle K_{X}}.

はXの会合定数、K t {displaystyle K_{t}} は

はリガンドがない場合のB状態とA状態の比（「遷移」）、K A B {displaystyle K_{AB}} はリガンドがない場合のB状態とA状態の比（「遷移」）。

および K B B {displaystyle K_{BB}}

は、両方のサブユニットがA状態にあるペアに対する隣接するサブユニットのペアの相対的な安定性である（KNF論文は、実際にはN s {displaystyle N_{s}} を提示することに注意されたい）。

、占有サイトの数で、ここでは4倍のY ¯ {displaystyle {}bar {Y}}} となる。

）となる。

MWC modelEdit

Monod-Wyman-Changeux model反応スキームは2つのプロトマーからなる蛋白質である。 プロトマーはリガンドに対してそれぞれ異なる親和性を持つ2つの状態で存在できる。 Lはリガンドがない場合の状態の比、cは親和力の比。

2つのプロトマーからなるタンパク質のMonod-Wyman-Changeuxモデルのエネルギーダイアグラムです。 リガンドのR状態への親和力が大きいということは、後者の結合が優先的に安定化することを意味する。

協調的アロステリック転移のMonod-Wyman-Changeux (MWC) モデルは、熱力学と三次元コンフォーメーションに基づいて協調性を探求し、さらに一歩進んだものである。 MWCモデルは、もともと同一サブユニットが対称的に配置され、それぞれが1つのリガンド結合部位を持つオリゴマー型タンパク質に対して定式化された。 この枠組みでは、アロステリックタンパク質の2つ（またはそれ以上）の相互変換可能なコンフォーメーションが熱的平衡状態で共存していることになる。 これらの状態は、しばしば緊張状態（Tense）と緩和状態（Raxed）と呼ばれ、リガンド分子に対する親和性が異なる。 この2つの状態の比率は、親和性の高い状態を安定化させるリガンド分子の結合によって制御される。 重要なのは、分子のすべてのサブユニットが同時に状態を変化させることで、これは「協調的変化」として知られている現象です。

アロステリック異性化定数Lは、リガンド分子が結合していないときの両方の状態の間の均衡を記述しています。 L = {displaystyle L={Thrac {Thracleft}{Left}}}

… 続きを読む Lが非常に大きいと、リガンドがない場合、タンパク質のほとんどがT状態で存在することになる。 Lが小さい（1に近い）場合、R状態はT状態とほぼ同程度の人口になる。 T状態とR状態からのリガンドの解離定数の比は定数cで記述される： c = K d R K d T {displaystyle c={frac {K_{d}^{R}}{K_{d}^{T}}}}

. c = 1の場合 {displaystyle c=1} .

の場合、R状態とT状態の両方がリガンドに対して同じ親和性を持ち、リガンドは異性化に影響を与えない。 cの値はリガンド結合時にT状態とR状態の間の平衡がどの程度変化するかも示しており、cが小さいほど一回の結合で平衡がR状態に移行する。 α = K d R {displaystyle \ ={frac {}{K_{d}^{R}}}} とすると、以下のようになります。

, fractional occupancyは次のように記述される。 Y ¯ = α ( 1 + α ) n – 1 + L c α ( 1 + c α ) n + L ( 1 + c α ) n {displaystyle {bar {Y}}={frac {alpha (1+alpha )^{n-}}} {displaystyle {bar {Y}}={frac {alpha (1+alpha )^{n-}}} {displaystyle {bar {Y}}={frac{{faculty}}}={faculty}}と表記する。1}+Lcphaalpha (1+cphaalpha )^{n-1}}{(1+Cphaalpha )^{n}+L(1+cphaalpha )^{n}}}}{(1+Cphaalpha )^{n}}}

アロステリック蛋白質のsigmoid Hill plotは、飽和度が高くなるとT状態（低親和性）からR状態（高親和性）への移行が進行すると解析することができる。 Hill plotの傾きも飽和度に依存し、変曲点では最大値をとる。 2つの漸近線とy軸の間の切片から、リガンドに対する両状態の親和性を決定することができる。

赤がMWC結合関数、緑が純粋なTとRの状態のヒルプロット。 コンフォメーションがTからRにシフトするにつれて，結合関数もまたシフトする。 x軸との切片は、RとT状態の微視的解離定数だけでなく、見かけの解離定数も示している。

タンパク質において、構造変化はしばしば活性、あるいは特定の標的に対する活性と関連している。 このような活性は、しばしば生理学的に関連するもの、または実験的に測定されるものである。 構造変化の程度は、状態関数Rによって記述されます。

, これはR {displaystyle R}の中に存在するタンパク質の割合を示すものである。｝

state. エネルギーダイアグラムが示すように、R ¯ {}{displaystyle {bar {R}}} {}は

リガンド分子の結合数が多くなると、増加する。 R ¯ {displaystyle {bar {R}} の式は、以下の通りです。｝

は、以下の通りである。 R ¯ = ( 1 + α ) n ( 1 + α ) n + L ( 1 + c α ) n {displaystyle {bar {R}}={frac {(1+alpha )^{n}}+L(1+c} )^{n}}}

MWCモデルの決定的側面は、Yに関するカーブ{displaystyle {bar {Y}}のことです。｝

and R¯ {displaystyle {bar {R}}} {}

は一致しない。すなわち、分数飽和はコンフォメーション状態（したがって活性）の直接的な指標とはならない。） さらに、結合の協同性と活性化の協同性の程度は非常に異なる場合がある。極端な例としては、バクテリアの鞭毛モーターがあり、結合のヒル係数は1.7、活性化のヒル係数は10.3である。 このような反応の超線形性を超感受性と呼ぶことがある。

アロステリックタンパク質が、R状態への親和性が高いターゲットに結合すると、ターゲット結合によりR状態がさらに安定化し、リガンド親和性が向上する。 一方、ターゲットがT状態に優先的に結合する場合、ターゲット結合はリガンド親和性にマイナスの影響を与える。 このような標的はアロステリックモジュレーターと呼ばれる。

MWCの枠組みはその開始以来、拡張され一般化されてきた。 例えば、2つ以上の状態を持つタンパク質、複数の種類のリガンドや複数の種類のアロステリックモジュレーターに結合するタンパク質、非同一サブユニットやリガンド結合部位を持つタンパク質に対応するためのバリエーションが提案されている

。